Trong một phòng thí nghiệm, nhiệt độ trong tủ sấy được điều khiển tăng từ 10°C, mỗi phút tăng 2°C trong 60 phút, sau đó giảm mỗi phút 3°C trong 40 phút. Hàm số biểu thị nhiệt độ (tính theo °C) trong theo thời gian \(t\) (tính theo phút) có dạng
\(T\left( t \right) = \left\{ {\begin{array}{*{20}{c}}{10 + 2t}&{khi\,\,0 \le t \le 60}\\{k - 3t}&{khi\,\,60 < t \le 100}\end{array}} \right.\) (\(k\) là hằng số).
Biết rằng, \(T\left( t \right)\) là hàm liên tục trên tập xác định. Tìm giá trị của \(k\).
Bước 1: Tìm tập xác định.
Bước 2: Tính \(T\left( {60} \right)\).
Bước 3: Tính \(\mathop {\lim }\limits_{t \to {{60}^ + }} T\left( t \right),\mathop {\lim }\limits_{t \to {{60}^ - }} T\left( t \right)\).
Bước 4: Giải phương trình \(\mathop {\lim }\limits_{t \to {{60}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ - }} T\left( t \right) = T\left( {60} \right)\) để tìm \(k\).
Hàm số \(T\left( t \right)\) có tập xác định là \(\left[ {0;100} \right]\).
Ta có: \(T\left( {60} \right) = 10 + 2.60 = 130\)
\(\begin{array}{l}\mathop {\lim }\limits_{t \to {{60}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ + }} \left( {k - 3t} \right) = k - 3.60 = k - 180\\\mathop {\lim }\limits_{t \to {{60}^ - }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ - }} \left( {10 + 2t} \right) = 10 + 2.60 = 130\end{array}\)
Để hàm số liên tục trên tập xác định thì hàm số phải liên tục tại điểm \({t_0} = 60\)
Khi đó: \(\mathop {\lim }\limits_{t \to {{60}^ + }} T\left( t \right) = \mathop {\lim }\limits_{t \to {{60}^ - }} T\left( t \right) = T\left( {60} \right) \Leftrightarrow k - 180 = 130 \Leftrightarrow k = 310\)
Vậy với \(k = 310\) thì hàm số \(T\left( t \right)\) liên tục trên tập xác định.

Các bài tập cùng chuyên đề
Một bảng giá cước taxi được cho như sau:
|
Giá mở cửa (0.5 km đầu) |
Giá cước các km tiếp theo đến 30 km |
Giá cước từ km thứ 31 |
|
10 000 đồng |
13 500 đồng |
11 000 đồng |
a) Viết công thức hàm số mô tả số tiền khách phải trả theo quãng đường di chuyển.
b) Xét tính liên tục của hàm số ở câu a.
Tính các giới hạn sau:
a) \(\mathop {{\rm{lim}}}\limits_{x \to 7} \frac{{\sqrt {x + 2} - 3}}{{x - 7}}\);
b) \(\mathop {{\rm{lim}}}\limits_{x \to 1} \frac{{{x^3} - 1}}{{{x^2} - 1}}\)
c) \(\mathop {{\rm{lim}}}\limits_{x \to 1} \frac{{2 - x}}{{{{\left( {1 - x} \right)}^2}}}\);
d) \(\mathop {{\rm{lim}}}\limits_{x \to - \infty } \frac{{x + 2}}{{\sqrt {4{x^2} + 1} }}\)
Tính các giới hạn một bên:
a) \(\mathop {\lim }\limits_{x \to {3^ + }} \frac{{{x^2} - 9}}{{\left| {x - 3} \right|}}\);
b) \(\mathop {\lim }\limits_{x \to {1^ - }} \frac{x}{{\sqrt {1 - x} }}\)
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}{x^2} + x + 1,\,\,x \ne 4\\2a + 1,\,\,x = 4\end{array} \right.\)
a) Với a = 0, xét tính liên tục của hàm số tại x = 4.
b) Với giá trị nào của a thì hàm số liên tục tại x = 4?
c) Với giá trị nào của a thì hàm số liên tục trên tập xác định của nó?
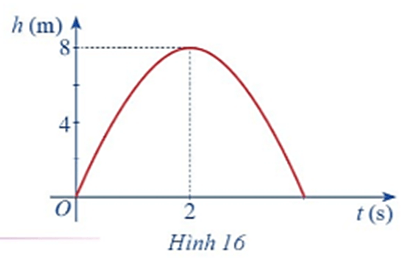
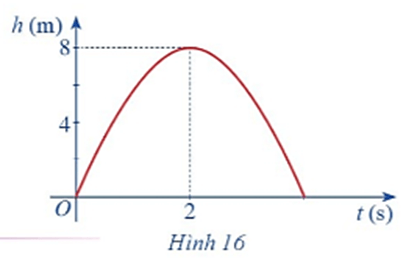
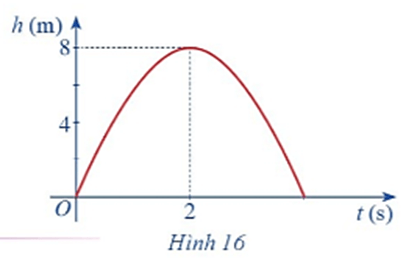
Hình 16 biểu thị độ cao h (m) của một quả bóng được đá lên theo thời gian t (s), trong đó \(h\left( t \right) = - 2{t^2} + 8t.\)
a) Chứng tỏ hàm số \(h\left( t \right)\) liên tục trên tập xác định.
b) Dựa vào đồ thị hãy xác định \(\mathop {\lim }\limits_{t \to 2} \left( { - 2{t^2} + 8t} \right).\)
Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{2x + a}&{{\rm{ }}x < 2}\\4&{{\rm{ }}x = 2}\\{ - 3x + b}&{{\rm{ }}\,x > 2}\end{array}} \right.\)
a) Với \(a = 0,b = 1\), xét tính liên tục của hàm số tại \(x = 2\).
b) Với giá trị nào của a, b thì hàm số liên tục tại \(x = 2\) ?
c) Với giá trị nào của a, b thì hàm số liên tục trên tập xác định?
Một bãi đậu xe ô tô đưa ra giá \(C\left( x \right)\) (đồng) khi thời gian đậu xe là \(x\) (giờ) như sau:
\(C\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{60000}&{khi\,\,0 < x \le 2}\\{100000}&{khi{\rm{ }}2 < x \le 4}\\{200000}&{khi{\rm{ }}4 < x \le 24}\end{array}} \right.\)
Xét tính liên tục của hàm số \(C\left( x \right)\).
Lực hấp dẫn do Trái Đất tác dụng lên một đơn vị khối lượng ở khoảng cách \(r\) ở tỉnh từ tâm của nó là
\(F\left( r \right) = \left\{ {\begin{array}{*{20}{c}}{\frac{{GM{\rm{r}}}}{{{R^3}}}}&{khi\,\,0 < x < R}\\{\frac{{GM}}{{{r^2}}}}&{khi\,\,r \ge R}\end{array}} \right.\)
trong đó \(M\) là khối lượng, \(R\) là bán kính của Trái Đất, \(G\) là hằng số hấp dẫn.
Hàm số \(F\left( r \right)\) có liên tục trên \(\left( {0; + \infty } \right)\) không?
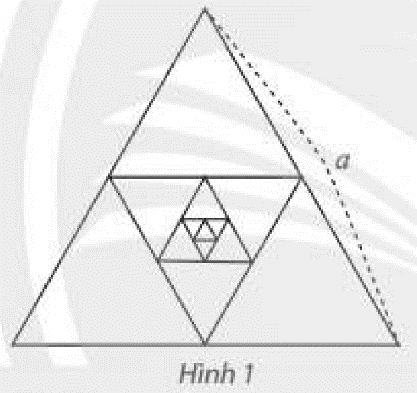
Cho tam giác đều có cạnh bằng \(a\), gọi là tam giác \({H_1}\). Nối các trung điểm của \({H_1}\) để tạo thành tam giác \({H_2}\). Tiếp theo, nối các trung điểm của \({H_1}\), để tạo thành tam giác \({H_3}\) (Hình 1). Cứ tiếp tục như vậy, nhận được dãy tam giác \({H_1},{H_2},{H_3},...\)
Tính tổng chu vi và tổng diện tích các tam giác của dãy.
Xét tính liên tục của các hàm số sau:
a) \(f\left( x \right) = {x^3} - {x^2} + 2\);
b) \(f\left( x \right) = \frac{{x + 1}}{{{x^2} - 4x}}\);
c) \(f\left( x \right) = \frac{{2x - 1}}{{{x^2} - x + 1}}\)
d) \(f\left( x \right) = \sqrt {{x^2} - 2x} \).
Xét tính liên tục của các hàm số sau:
a) \(f\left( x \right) = \frac{{\tan x}}{{\sqrt {1 - {x^2}} }}\);
b) \(f\left( x \right) = \frac{1}{{\sin x}}\).
Cho hai hàm số \(f\left( x \right) = \left\{ \begin{array}{l}2 - x\;\;\;khi\;x < 1\\{x^2} + x\;khi\;x \ge 1\end{array} \right.\) và \(g\left( x \right) = \left\{ \begin{array}{l}2x - {x^2}\;khi\;x < 1\\ - {x^2} + a\;khi\;x \ge 1\end{array} \right.\).
Tìm giá trị của tham số a sao cho \(h\left( x \right) = f\left( x \right) + g\left( x \right)\) liên tục tại \(x = 1\).
Cho hàm số \(y = f\left( x \right) = \left\{ \begin{array}{l}{x^2} + ax + b\;khi\;\left| x \right| < 2\\x\left( {2 - x} \right)\;\;\;\;\,khi\;\left| x \right| \ge 2\end{array} \right.\). Tìm giá trị của các tham số a và b sao cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\).
Chứng minh rằng phương trình:
a) \({x^3} + 2x - 1 = 0\) có nghiệm thuộc khoảng \(\left( { - 1;1} \right)\);
b) \(\sqrt {{x^2} + x} + {x^2} = 1\) có nghiệm thuộc khoảng \(\left( {0;1} \right)\).
Cho nửa đường tròn đường kính \(AB = 2\). Đường thẳng d thay đổi luôn đi qua A, cắt nửa đường tròn tại C và tạo với đường thẳng AB góc \(\alpha \left( {0 < \alpha < \frac{\pi }{2}} \right)\). Kí hiệu diện tích tam giác ABC là \(S\left( \alpha \right)\) (phụ thuộc vào \(\alpha \)). Xét tính liên tục của hàm số \(S\left( \alpha \right)\) trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\) và tính các giới hạn \(\mathop {\lim }\limits_{\alpha \to {0^ + }} S\left( \alpha \right)\); \(\mathop {\lim }\limits_{\alpha \to {{\frac{\pi }{2}}^ - }} S\left( \alpha \right)\)
Biết rằng phương trình \({x^3} - 2x - 3 = 0\) chỉ có một nghiệm. Phương trình này có nghiệm trong khoảng nào sau đây?
A. \(\left( { - 1;0} \right)\).
B. \(\left( {0;1} \right)\).
C. \(\left( {1;2} \right)\).
D. \(\left( {2;3} \right)\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - 9}}{{\left| {x + 3} \right|}}\;khi\;x \ne - 3\\\;\;\;\;a\;\;\;\;\,khi\;x = - 3\end{array} \right.\)
a) Tìm \(\mathop {\lim }\limits_{x \to - {3^ + }} f\left( x \right) - \mathop {\lim }\limits_{x \to - {3^ - }} f\left( x \right)\).
b) Với giá trị nào của a thì hàm số liên tục tại \(x = - 3\).
Cho hàm số \(f\left( x \right) = \frac{{2x + 1}}{{x - 3}}\).
a) Xét tính liên tục của hàm số đã cho.
b) Tìm các giới hạn \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right);\mathop {\lim }\limits_{x \to - \infty } f\left( x \right);\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right);\mathop {\lim }\limits_{x \to 3} f\left( x \right)\).
Chứng minh rằng phương trình \({x^5} + 3{x^2} - 1 = 0\) trong mỗi khoảng \(\left( { - 2; - 1} \right);\left( { - 1;0} \right)\) và \(\left( {0;1} \right)\) đều có ít nhất một nghiệm.
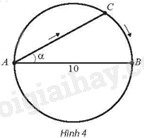
Tại một bể bơi có dạng hình tròn có đường kính \(AB = 10m\), một người xuất phát từ A bơi thẳng theo dây cung AC tạo với đường kính AB một góc \(\alpha \left( {0 < \alpha < \frac{\pi }{2}} \right)\), rồi chạy bộ theo cung nhỏ CB đến điểm B (Hình 4). Gọi \(S\left( \alpha \right)\) là quãng đường người đó đã di chuyển.
a) Viết công thức tính \(S\left( \alpha \right)\) theo \(\alpha \left( {0 < \alpha < \frac{\pi }{2}} \right)\).
b) Xét tính liên tục của hàm số \(y = S\left( \alpha \right)\) trên khoảng \(\left( {0;\frac{\pi }{2}} \right)\).
c) Tính các giới hạn \(\mathop {\lim }\limits_{\alpha \to {0^ + }} S\left( \alpha \right)\) và \(\mathop {\lim }\limits_{\alpha \to {{\frac{\pi }{2}}^ + }} S\left( \alpha \right)\).
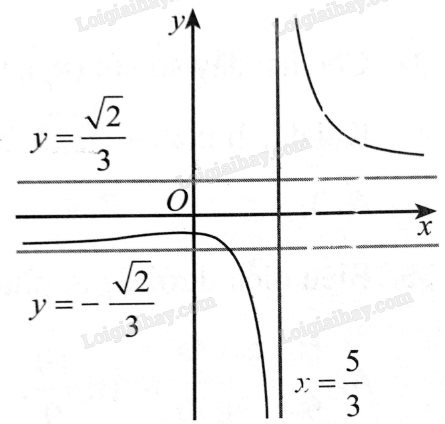
Quan sát đồ thị hàm số trong hình dưới đây và cho biết hàm số đó có liên tục:
a) Tại \(x = \frac{5}{3}\) hay không.
b) Trên khoảng \(\left( { - \infty ;0} \right)\) hay không.
Xét tính liên tục của các hàm số sau:
a) \(f\left( x \right) = - {x^2} + \cos x\)
b) \(g\left( x \right) = 3{x^3} + 2 - \frac{3}{{x + 2}}\)
c) \(h\left( x \right) = \frac{{2x + 5}}{{x + 2}} + \frac{{3x - 1}}{{2x - 4}}\)
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}{x^2} - x{\rm{ }}\left( {x \ge 1} \right)\\x + a{\rm{ }}\left( {x < 1} \right)\end{array} \right.\)
a) Với \(a = 2\), xét tính liên tục của hàm số tại \(x = 1\).
b) Tìm \(a\) để hàm số liên tục trên \(\mathbb{R}\).
Theo quyết định số 2019/QĐ-BĐVN ngày 01/11/2018 của Tổng công ty Bưu điện Việt Nam, giá cước dịch vụ Bưu chính phổ cập đối với dịch vụ thư cơ bản và bưu thiếp trong nước có khối lượng đến 250 g như trong bảng sau:
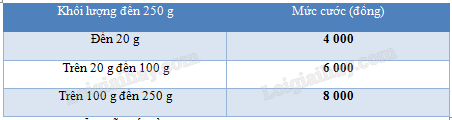
a) Hãy biểu diễn số tiền phải trả khi sử dụng dịch vụ thư cơ bản và bưu thiếp theo khối lượng của thư cơ bản và bưu thiếp.
b) Hàm số trên có liên tục trên tập xác định hay không?
Hàm số nào sau đây KHÔNG liên tục trên tập xác định của nó?
A. \(y = x\)
B. \(y = \frac{1}{x}\)
C. \(y = \sin x\)
D. \(y = \left\{ \begin{array}{l}0{\rm{ }}\left( {x < 0} \right)\\1{\rm{ }}\left( {x \ge 0} \right)\end{array} \right.\)
Hàm số \(y = \tan x\) gián đoạn tại bao nhiêu điểm trên khoảng \(\left( {0;2\pi } \right)\)?
A. 0
B. 1
C. 2
D. 3
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{{{x^2} - 4}}{{x - 2}}{\rm{ }}\left( {x \ne 2} \right)\\a{\rm{ }}\left( {x = 2} \right)\end{array} \right.\).
Tìm \(a\) để hàm số liên tục trên \(\mathbb{R}\).
Chứng tỏ rằng các phương trình sau có nghiệm trong khoảng tương ứng:
a) \({x^2} = \sqrt {x + 1} \), trong khoảng \(\left( {1;2} \right)\)
b) \(\cos x = x,\) trong khoảng \(\left( {0;1} \right)\)
Cho phương trình \({x^7} + {x^5} = 1\). Mệnh đề đúng là
A. Phương trình có nghiệm âm
B. Phương trình có nghiệm trong khoảng \((0;1)\).
C. Phương trình có nghiệm trong khoảng \((1;2)\)
D. Phương trình vô nghiệm
Cho hàm số \(f(x) = \left\{ \begin{array}{l}\frac{1}{x}\,\,{\rm{khi}}\,\,x \ne 0\\2\,\,\,{\rm{khi}}\,\,x = 0\end{array} \right.\)
a) Chứng minh rằng \(f( - 1).f(1) < 0\).
b) Chứng minh rằng phương trình \(f(x) = 0\) không có nghiệm thuộc khoảng \(( - 1;1)\).
c) Có kết luận gì về tính liên tục của hàm số \(f(x)\) trên đoạn \([ - 1;1]\).







Danh sách bình luận