Xét tính liên tục của hàm số \(y = \sqrt {{x^2} - 4} \).
Để tính xét tính liên tục của hàm số, ta tìm những khoảng xác định của hàm số đó.
ĐKXĐ: \({x^2} - 4 \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \ge 2\\x \le - 2\end{array} \right.\)
Vậy hàm số có TXĐ: \(D = \left( { - \infty ; - 2} \right] \cup \left[ {2; + \infty } \right)\).
Hàm số \(y = \sqrt {{x^2} - 4} \) là hàm số căn thức nên nó liên tục trên các nửa khoảng \(\left( { - \infty ; - 2} \right)\) và \(\left( {2; + \infty } \right)\).
Ta có: \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \sqrt {{x^2} - 4} = \sqrt {{2^2} - 4} = 0 = f\left( 2 \right)\)
\(\mathop {\lim }\limits_{x \to - {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to - {2^ + }} \sqrt {{x^2} - 4} = \sqrt {{{\left( { - 2} \right)}^2} - 4} = 0 = f\left( { - 2} \right)\)
Vậy hàm số \(y = \sqrt {{x^2} - 4} \) liên tục trên các nửa khoảng \(\left( { - \infty ; - 2} \right]\) và \(\left[ {2; + \infty } \right)\).

Các bài tập cùng chuyên đề
Một người lái xe từ địa điểm A đến địa điểm B trong thời gian 3 giờ. Biết quãng đường từ A đến B dài 180 km. Chứng tỏ rằng có ít nhất một thời điểm trên hành trình, xe chạy với vận tốc 60 km/h.

Cho hai hàm số \(f\left( x \right) = {x^2}\) và \(g\left( x \right) = - x + 1\)
a) Xét tính liên tục của hai hàm số trên tại \(x = 1\)
b) Tính \(L = \mathop {{\rm{lim}}}\limits_{x \to 1} \;\left[ {f\left( x \right) + g\left( x \right)} \right]\) và so sánh L với \(f\left( 1 \right) + g\left( 1 \right)\).
Cho \(f\left( x \right)\) và \(g\left( x \right)\) là các hàm số liên tục tại \(x = 1\). Biết \(f\left( 1 \right) = 2\) và \(\mathop {{\rm{lim}}}\limits_{x \to {1}} \left[ {2f\left( x \right) - g\left( x \right)} \right] = 3\). Tính \(g\left( 1 \right)\).
Cho \(f\left( x \right)\) và \(g\left( x \right)\) là các hàm số liên tục tại \(x = 1\). Biết \(f\left( 1 \right) = 2\) và \(\mathop {{\rm{lim}}}\limits_{x \to {1}} \left[ {2f\left( x \right) - g\left( x \right)} \right] = 3\). Tính \(g\left( 1 \right)\).
Xét tính liên tục của hàm số \(f\left( x \right) = \sin x + \cos x\) trên \(\mathbb{R}.\)
Cho hai hàm số \(f\left( x \right) = {x^3} + x\) và \(g\left( x \right) = {x^2} + 1\,\,\left( {x \in \mathbb{R}} \right).\) Hãy cho biết:
a) Hai hàm số \(f\left( x \right),g\left( x \right)\) có liên tục tại \(x = 2\) hay không.
b) Các hàm số \(f\left( x \right) + g\left( x \right);f\left( x \right) - g\left( x \right);f\left( x \right).g\left( x \right);\frac{{f\left( x \right)}}{{g\left( x \right)}}\) có liên tục tại \(x = 2\) hay không.
Hàm số \(f\left( x \right) = \frac{{x + 2}}{{x - 8}}\) có liên tục trên mỗi khoảng \(\left( { - \infty ;8} \right),\left( {8; + \infty } \right)\) hay không?
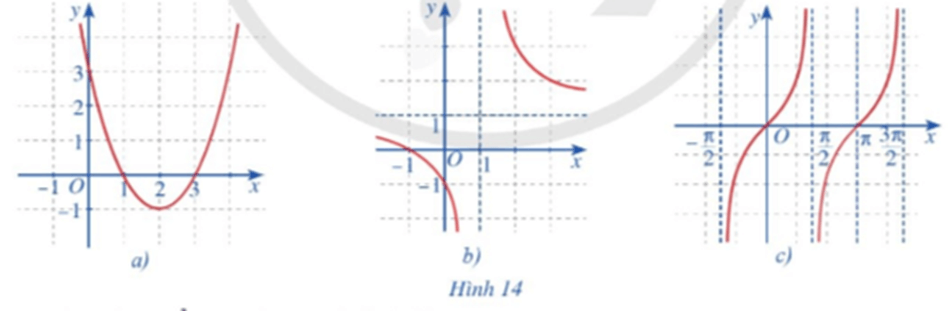
Quan sát đồ thị các hàm số: \(y = {x^2} - 4x + 3\) (Hình 14a);
\(y = \frac{{x + 1}}{{x - 1}}\,\,\left( {x \ne 1} \right)\) (Hình 14b);
\(y = \tan x\) (Hình 14c).
Và nêu nhận xét về tính liên tục của mỗi hàm số đó trên từng khoảng của tập xác định.
Bạn Nam cho rằng: “Nếu hàm số \(y = f\left( x \right)\) liên tục tại điểm \({x_0},\) còn hàm số \(y = g\left( x \right)\) không liên tục tại \({x_0},\) thì hàm số \(y = f\left( x \right) + g\left( x \right)\) không liên tục tại \({x_0}\)”. Theo em, ý kiến của bạn Nam đúng hay sai? Giải thích.
Một hãng taxi đưa ra giá cước \(T\left( x \right)\) (đồng) khi đi quãng đường \(x\) (km) cho loại xe 4 chỗ như sau:
\(T\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{10000}&{khi\,\,0 < x \le 0,7}\\{ - 10000 + \left( {x - 0,7} \right).14000}&{khi{\rm{ }}0,7 < x \le 20}\\{280200 + \left( {x--20} \right).12000}&{khi{\rm{ }}x > 20}\end{array}} \right.\)
Xét tính liên tục của hàm số \(T\left( x \right)\).
Cho hàm số \(f\left( x \right) = \left\{ {\begin{array}{*{20}{c}}{\frac{{{x^2} - 2x}}{x}}&{khi\,\,x \ne 0}\\a&{khi\,\,x = 0}\end{array}} \right.\).
Tìm \(a\) để hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\).
Cho hai hàm số \(y = f\left( x \right) = \frac{1}{{x - 1}}\) và \(y = g\left( x \right) = \sqrt {4 - x} \).
a) Tìm tập xác định của mỗi hàm số đã cho.
b) Mỗi hàm số trên liên tục trên những khoảng nào? Giải thích.
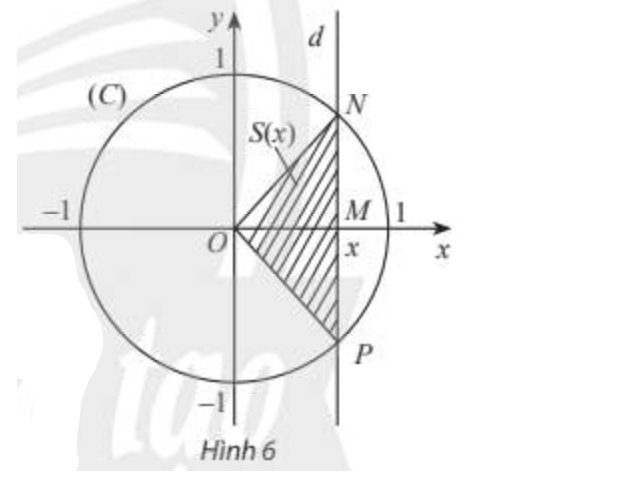
Trong mặt phẳng toạ độ \(Oxy\), cho đường tròn \(\left( C \right)\) tâm \(O\), bán kính bằng 1. Một đường thẳng \(d\) thay đổi, luôn vuông góc với trục hoành, cắt trục hoành tại điểm \(M\) có hoành độ \(x\left( { - 1 < x < 1} \right)\) và cắt đường tròn \(\left( C \right)\) tại các điểm \(N\) và \(P\) (xem Hình 6).
a) Viết biểu thức \(S\left( x \right)\) biểu thị diện tích của tam giác \(ONP\).
b) Hàm số \(y = S\left( x \right)\) có liên tục trên \(\left( { - 1;1} \right)\) không? Giải thích.
c) Tìm các giới hạn \(\mathop {\lim }\limits_{x \to {1^ - }} S\left( x \right)\) và \(\mathop {\lim }\limits_{x \to - {1^ + }} S\left( x \right)\).
Xét tính liên tục của các hàm số:
a) \(y = \sqrt {{x^2} + 1} + 3 - x\);
b) \(y = \frac{{{x^2} - 1}}{x}.\cos x\).
Cho hai hàm số \(y = f\left( x \right) = \frac{1}{{x - 1}}\) và \(y = g\left( x \right) = \sqrt {4 - x} \).
Hàm số \(y = f\left( x \right) + g\left( x \right)\) có liên tục tại \(x = 2\) không? Giải thích.
Cho hàm số \(f\left( x \right) = 2x - \sin x,g\left( x \right) = \sqrt {x - 1} \).
Xét tính liên tục hàm số \(y = f\left( x \right).g\left( x \right)\) và \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\).
Cho hai hàm số \(f\left( x \right) = x - 1\) và \(g\left( x \right) = {x^2} - 3x + 2\). Xét tính liên tục của các hàm số:
a) \(y = f\left( x \right).g\left( x \right)\);
b) \(y = \frac{{f\left( x \right)}}{{g\left( x \right)}}\);
c) \(y = \frac{1}{{\sqrt {f\left( x \right) + g\left( x \right)} }}\).







Danh sách bình luận