Cho điểm A không thuộc đường thẳng d. Lấy hai điểm phân biệt B và C thuộc đường thẳng d (Hình 18).
a) Mặt phẳng đi qua ba điểm A, B, C có đi qua đường thẳng d hay không?
b) Có bao nhiêu mặt phẳng đi qua điểm A và đường thẳng d?
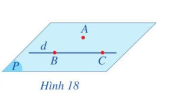
Cho điểm A không thuộc đường thẳng d. Khi đó, qua điểm A và đường thẳng d có một và chỉ một mặt phẳng
a) Mặt phẳng đi qua ba điểm A, B, C đi qua đường thẳng d
b) Có một và chỉ một mặt phẳng đi qua điểm A và đường thẳng d
Các bài tập cùng chuyên đề
Để tránh cho cửa ra vào không bị va đập vào các đồ dùng xung quanh (do mở cửa quá mạnh hoặc do gió to đập cửa), người ta thường sử dụng một phụ kiện là hít cửa nam châm. Hãy giải thích tại sao khi cửa được hút tới vị trí của nam châm thì cánh cửa được giữ cố định.
Trong Ví dụ 4, vẽ một đường thẳng c cắt cả hai đường thẳng a và b. Xác định giao tuyến của hai mặt phẳng: mp (S, a) và mp (S, c); mp (S, b) và mp (S, c).
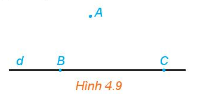
Cho đường thẳng d và điểm A không thuộc d. Trên đường thẳng d lấy hai điểm phân biệt B, C (H.4.9). Mặt phẳng (ABC) có chứa điểm A và đường thẳng d hay không? Mặt phẳng (ABC) có chứa hai đường thẳng AB và BC hay không?
Trong mặt phẳng (P) cho tam giác ABC. Điểm D không thuộc mặt phẳng (P). Hỏi qua hai đường thẳng AD và BC có xác định được một mặt phẳng không?
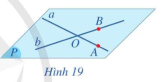
Cho hai đường thẳng a và b cắt nhau tại O. Lấy điểm A trên đường thẳng a (A khác O), lấy điểm B trên đường thẳng b (B khác O) (Hình 19).
a) Mặt phẳng đi qua ba điểm A, B, O có đi qua hai đường thẳng a và b hay không?
b) Có bao nhiêu mặt phẳng đi qua hai đường thẳng a và b?
Trong xây dựng, người ta thường dùng máy quét tia laser để kẻ các đường thẳng trên tường hoặc sàn nhà. Tìm giao tuyến của mặt phẳng tạo bởi các tia laser \(OA\) và \(OB\) với các mặt tường trong Hình 29.
Giải thích tại sao ghế bốn chân có thể bị khập khiễng còn ghế ba chân thì không.
Cho hai đường thẳng \(a\) và \(b\) cắt nhau tại \(O\) và điểm \(M\) không thuộc \(mp\left( {a,b} \right)\).
a) Tìm giao tuyến của hai mặt phẳng \(\left( {M,a} \right)\) và \(\left( {M,b} \right)\).
b) Lấy \(A,B\) lần lượt là hai điểm trên \(a,b\) và khác với điểm \(O\). Tìm giao tuyến của \(\left( {MAB} \right)\) và \(mp\left( {a,b} \right)\).
c) Lấy điểm \(A'\) trên đoạn \(MA\) và điểm \(B'\) trên đoạn \(MB\) sao cho đường thẳng \(A'B'\) cắt \(mp\left( {a,b} \right)\) tại \(C\). Chứng minh ba điểm \(A,B,C\) thẳng hàng.
Hai đường thẳng phân biệt \(a\) và \(b\) cắt nhau tại điểm \(O\). Trên \(a,b\) lấy lần lượt hai điểm \(M,N\) khác \(O\). Gọi \(\left( P \right)\) là mặt phẳng đi qua ba điểm \(M,N,O\) (Hình 25). Mặt phẳng \(\left( P \right)\) có chứa cả hai đường thẳng \(a\) và \(b\) không? Giải thích.
Cho đường thẳng \(a\) và điểm \(A\) không nằm trên \(a\). Trên \(a\) lấy hai điểm \(B,C\). Đường thẳng \(a\) có nằm trong mặt phẳng \(\left( {ABC} \right)\) không? Giải thích.
Các yếu tố nào sau đây xác định một mặt phẳng?
Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
Trên mặt phẳng cho bốn điểm A, B, C, D như hình vẽ. Ba điểm nào sau đây không xác định một mặt phẳng?
Cho mặt phẳng \(\left( \alpha \right)\), cho 4 điểm $A,\,\,B,\,\,C,\,\,D$ trong đó không có ba điểm nào thẳng hàng. Điểm $S$ không thuộc mặt phẳng \(\left( \alpha \right)\). Có mấy mặt phẳng tạo bởi $S$ và 2 trong 4 điểm nói trên?
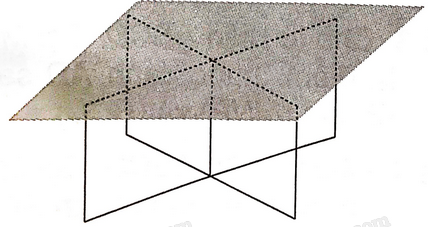
Một số chiếc bàn có thiết kế khung sắt là hai hình chữ nhật có thể xoay quanh một trục, mặt bàn là một tấm gỗ phẳng được đặt lên phần khung như trong hình 4.6. Tính chất hình học nào giải thích việc mặt bàn có thể được giữ cố định bởi khung sắt? (Giả sử khung sắt chắc chắn và được đặt cân đối).
Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
A. Ba điểm.
B. Một điểm và một đường thẳng.
C. Hai đường thẳng cắt nhau.
D. Bốn điểm.
Trong các khẳng định sau, khẳng định nào đúng?
