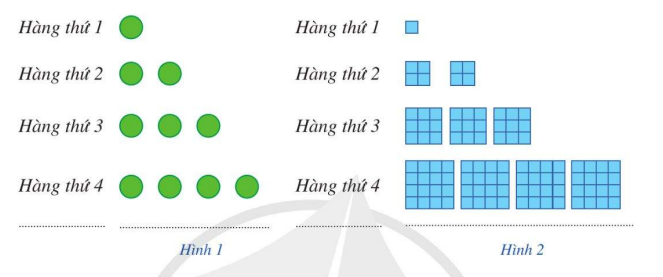
a) Gọi \({u_n}\) là số chấm ở hàng thứ n trong Hình 1. Dự đoán công thức của số hạng tổng quát cho dãy số \(\left( {{u_n}} \right)\)
b) Gọi \({v_n}\) là tổng diện tích của các hình tô màu ở hành thứ n trong Hình 2 (Mỗi ô vuông nhỏ là một đơn vị diện tích). Dự đoán công thức của số hàng tổng quát cho dãy số \(\left( {{v_n}} \right)\)
Dựa vào kiến thức đã học để xác định
a) Ta có: \({u_1} = 1,{u_2} = 2,{u_3} = 3\)
Dự đoán \({u_n} = n\)
b) Ta có: \(\begin{array}{l}{v_1} = 1\\{v_2} = 8 = {2^3}\\{v_3} = 27 = {3^3}\\{v_4} = 64 = {4^3}\end{array}\)
Dự đoán: \({v_n} = {n^3}\)
Các bài tập cùng chuyên đề
a) Viết năm số hạng đầu của dãy số \(\left( {{u_n}} \right)\) với số hạng tổng quát \({u_n} = n!.\).
b) Viết năm số hạng đầu của dãy số Fibonacci \(\left( {{F_n}} \right)\) cho bởi hệ thức truy hồi
\(\{ {F_1} = 1,\;{F_2} = 1\;{F_n} = {F_{n - 1}} + {F_{n - 2}}\;\left( {n \ge 3} \right)\;\).
Xét dãy số \(({u_n})\) gồm tất cả các số nguyên dương chia hết cho 5:
\(5;10;15;20;25;30; \ldots \)
a) Viết công thức số hạng tổng quát \({u_n}\) của dãy số.
b) Xác định số hạng đầu và viết công thức tính số hạng thứ n theo số hạng thứ n – 1 của dãy số. Công thức thu được gọi là hệ thức truy hồi.
Viết năm số hạng đầu và số hạng thứ 100 của các dãy số \(\left( {{u_n}} \right)\) có số hạng tổng quát cho bởi:
a) \({u_n} = 3n - 2\)
b) \({u_n} = {3.2^n}\)
c) \({u_n} = {\left( {1 + \frac{1}{n}} \right)^n}\)
Dãy số \(\left( {{u_n}} \right)\)cho bởi hệ thức truy hồi: \({u_1} = 1,\;\;\;{u_n} = n.{u_{n - 1}}\) với \(n \ge 2\)
a) Viết năm số hạng đầu của dãy số.
b) Dự đoán công thức số hạng tổng quát \({u_n}\).
Viết số hạng tổng quát của dãy số tăng gồm tất cả các số nguyên dương mà mỗi số hạng của nó:
a) Đều chia hết cho 3;
b) Khi chia cho 4 dư 1.
Ông An gửi tiết kiệm 100 triệu đồng kì hạn 1 tháng với lãi suất 6% một năm theo hình thức tính lãi kép. Số tiền (triệu đồng) của ông An thu được sau n tháng được cho bởi công thức:
\({A_n} = 100{\left( {1 + \frac{{0,06}}{{12}}} \right)^n}\)
a) Tìm số tiền ông An nhận được sau tháng thứ nhất, sau tháng thứ hai
b) Tìm số tiền ông An nhận được sau 1 năm
Chị Hương vay trả góp một khoản tiền 100 triệu đồng và đồng ý trả dần 2 triệu đồng mỗi tháng với lãi suất 0,8% số tiền còn lại của mỗi tháng.
Gọi \({A_n}\;\left( {n \in N} \right)\) là số tiền còn nợ (triệu đồng) của chị Hương sau n tháng.
a) Tìm lần lượt \({A_0},\;{A_1},{A_2},{A_3},{A_4},{A_5},{A_6}\) để tính số tiền còn nợ của chị Hương sau 6 tháng.
b) Dự đoán hệ thức truy hồi đối với dãy số \(\left( {{A_n}} \right)\)
Cho dãy số \((u_n)\) với \(u_n=\frac{n-3}{3n+1}\) . Tìm \(u_{33}, u_{333}\) và viết dãy số dưới dạng khai triển.
- Dãy số: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 (1)
- Dãy số \(\left( {{u_n}} \right)\) được xác định bởi: Với mỗi số tự nhiên \(n \ge 1,{u_n}\) là số thập phân hữu hạn có phần số nguyên là 1 và phần thập phân là n chữ số thập phân đầu tiên đứng sau “,” của số \(\sqrt 2 \). Cụ thể là:
\({u_1} = 1,4;{u_2} = 1,41;{u_3} = 1,414;{u_4} = 1,4142;{u_5} = 1,41421;...\left( 2 \right)\)
- Dãy số \(\left( {{u_n}} \right)\) với \({u_n} = {\left( { - 2} \right)^n}\) (3)
- Dãy số \(\left( {{u_n}} \right)\) được xác định bởi: \({u_1} = 1\) và \({u_n} = {u_{n - 1}} + 2\) với mọi \(n \ge 2\,\,\left( 4 \right)\)
a) Hãy nêu cách xác định mỗi số hạng của lần lượt các dãy số (1), (2), (3), (4)
b) Từ đó hãy cho biết dãy số có thể cho bằng những cách nào.
Viết năm số hạng đầu của mỗi dãy số có số hạng tổng quát \({u_n}\) cho bởi công thức sau:
a) \({u_n} = 2{n^2} + 1\)
b) \({u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{{2n - 1}}\)
c) \({u_n} = \frac{{{2^n}}}{n}\)
d) \({u_n} = {\left( {1 + \frac{1}{n}} \right)^n}\)
Một chồng cột gỗ được xếp thành các lớp, hai lớp liên tiếp hơn kém nhau 1 cột gỗ (Hình 1). Gọi \({u_n}\) là số cột gỗ nằm ở lớp thứ 2 tính từ trên xuống và cho biết lớp trên cùng có 14 cột gỗ. Hãy xác định dãy số \(\left( {{u_n}} \right)\) bằng hai cách:
a) Viết công thức số hạng tổng quát \({u_n}\).
b) Viết hệ thức truy hồi.
Cho dãy số \(\left( {{u_n}} \right)\) xác định bởi: \(\left\{ \begin{array}{l}{u_1} = 3\\{u_{n + 1}} = 2{u_n}\left( {n \ge 1} \right)\end{array} \right.\).
a) Chứng minh \({u_2} = 2.3;{u_3} = {2^2}.3;{u_4} = {2^3}.3\).
b) Dự đoán công thức số hạng tổng quát của dãy số \(\left( {{u_n}} \right)\).
Cho các dãy số \(\left( {{a_n}} \right),\left( {{b_n}} \right),\left( {{c_n}} \right),\left( {{d_n}} \right)\) được xác định như sau.
• \({a_1} = 0;{a_2} = 1;{a_3} = 2;{a_4} = 3;{a_5} = 4\).
• \({b_n} = 2n\).
• \(\left\{ \begin{array}{l}{c_1} = 1\\{c_n} = {c_{n - 1}} + 1\left( {n \ge 2} \right)\end{array} \right.\).
• \({d_n}\) là chu vi của đường tròn có bán kính \(n\).
Tìm bốn số hạng đầu tiên của các dãy số trên.
Tìm \({u_2},{u_3}\) và dự đoán công thức số hạng tổng quát \({u_n}\) của dãy số:
\(\left\{ \begin{array}{l}{u_1} = 1\\{u_{n + 1}} = \frac{{{u_n}}}{{1 + {u_n}}}\left( {n \ge 1} \right)\end{array} \right.\)
Cho dãy số \(\left( {{u_n}} \right)\) với \({u_n} = \frac{1}{{1.2}} + \frac{1}{{2.3}} + ... + \frac{1}{{n\left( {n + 1} \right)}}\). Tìm \({u_1},{u_2},{u_3}\) và dự đoán công thức số hạng tổng quát \({u_n}\).
Cho dãy số: \(\frac{1}{3};\frac{1}{{{3^2}}};\frac{1}{{{3^3}}};\frac{1}{{{3^4}}};\frac{1}{{{3^5}}};...\). Số hạng tổng quát của dãy số này là:
A. \({u_n} = \frac{1}{3}.\frac{1}{{{3^{n + 1}}}}\).
B. \({u_n} = \frac{1}{{{3^{n + 1}}}}\).
C. \({u_n} = \frac{1}{{{3^n}}}\).
D. \({u_n} = \frac{1}{{{3^{n - 1}}}}\).
Cho dãy số có các số hạng đầu là \(0;\frac{1}{2};\frac{2}{3};\frac{3}{4};\frac{4}{5};...\) Số hạng tổng quát của dãy số là:
Với \(n \in {\mathbb{N}^*}\), cho dãy số \(\left( {{u_n}} \right)\) có số hạng tổng quát \({u_n} = {n^2} - 1\). Năm số hạng đầu tiên của dãy số này là
Với \(n \in {\mathbb{N}^*}\), cho dãy số \(\left( {{u_n}} \right)\) gồm các số nguyên dương chia hết cho \(7\) là \(7\), \(14\), \(21\), \(28\), … Công thức số hạng tổng quát của dãy số này là
Mỗi dãy số \(\left( {{u_n}} \right)\) sau có phải là một cấp số cộng không? Nếu có, hãy tìm số hạng đầu và công sai của nó:
a) \({u_n} = 4 - 3n\);
b) \({u_n} = {n^2} + 1;\);
c) \({u_n} = 2n + 5\);
d) \({u_1} = 3,{u_{n + 1}} = {u_n} + n\).
Cho dãy số \(\left( {{u_n}} \right)\) biết \({u_1} = 2\) và \({u_n} = \frac{{{u_{n - 1}} + 1}}{2}\) với mọi \(n \ge 2\). Ba số hạng đầu tiên của dãy số lần lượt là:
A. \(2;{\rm{ 1; }}\frac{3}{2}\)
B. \(2;{\rm{ }}\frac{3}{2}{\rm{; }}\frac{5}{2}\)
C. \(2;{\rm{ }}\frac{3}{2}{\rm{; }}\frac{5}{4}\)
D. \(2;{\rm{ }}\frac{3}{2};{\rm{ 2}}\)
Cho dãy số \(\left( {{u_n}} \right)\) biết \({u_n} = \frac{{2{n^2} - 1}}{{{n^2} + 2}}\). Số hạng \({u_{10}}\) là:
A. \(\frac{{19}}{{12}}\)
B. \(\frac{{33}}{{34}}\)
C. \(\frac{{199}}{{102}}\)
D. \(\frac{3}{4}\)
Cho dãy số \(\left( {{u_n}} \right)\) biết \({u_n} = \frac{{n + 1}}{{3n - 2}}\). Với \({u_k} = \frac{8}{{19}}\) là số hạng của dãy số thì \(k\) bằng:
A. 8
B. 7
C. 9
D. 6
Cho dãy số \(\left( {{u_n}} \right)\) biết \({u_n} = {3^n}\). Số hạng \({u_{n + 1}}\) bằng:
A. \({3^n}.3\)
B. \({3^n} + 3\)
C. \({3^n} + 1\)
D. \(3\left( {n + 1} \right)\)
Cho dãy số \(\left( {{u_n}} \right)\) biết \({u_1} = 2\) và \({u_n} = \sqrt {2 + u_{n - 1}^2} \) với mọi \(n \ge 2\). Viết năm số hạng đầu của dãy số và dự đoán công thức của số hạng tổng quát \({u_n}\).
Cho dãy số \(\left( {{u_n}} \right)\) biết \({u_n} = {5^n} - n\). Số hạng \({u_{n + 1}}\) là:
A. \({5^{n + 1}} - n - 1\)
B. \({5^{n + 1}} - n + 1\)
C. \({5^n} - n + 1\)
D. \({5^n} - n - 1\)
Dự đoán công thức số hạng tổng quát của dãy số \(\left( {{u_n}} \right)\), biết \(\left\{ \begin{array}{l}{u_1} = - 2\\{u_{n + 1}} = - 2 - \frac{1}{{{u_n}}}\end{array} \right.\).
Cho dãy số $\left( {{u_n}} \right)$, với ${u_n} = {\left( {\frac{{n - 1}}{{n + 1}}} \right)^{2n + 3}}$. Tìm số hạng ${u_{n + 1}}$.
Cho dãy số \(\left( {{u_n}} \right)\), biết \(\left\{ \begin{array}{l}{u_1} = 1\\{u_{n + 1}} = {u_n} + n\end{array} \right.\) với \(n \ge 1\). Số hạng thứ 3 của dãy số đó là:
Dãy số \( - 1;1; - 1;1; - 1; \cdots \) có số hạng tổng quát là công thức nào dưới đây?
