Gọi S là diện tích hình phẳng giới hạn bởi các đường $y = {x^3},y = 2 - x$ và $y = 0$. Mệnh đề nào sau đây là đúng?
-
A.
$S = \int\limits_0^1 {{x^3}} d{\rm{x + }}\int\limits_1^2 {\left( {x - 2} \right)} d{\rm{x}}$
-
B.
$S = \left| {\int\limits_0^2 {\left( {{x^3} + x - 2} \right)} d{\rm{x}}} \right|$
-
C.
$S = \dfrac{1}{2} + \int\limits_0^1 {{x^3}} d{\rm{x }}$
-
D.
$S = \int\limits_0^1 {\left| {{x^3} + x - 2} \right|} d{\rm{x}}$
Diện tích hình phẳng giới hạn bởi một đường cong
Nếu hàm số $y = f\left( x \right)$ liên tục trên đoạn $\left[ {a;b} \right]$ thì diện tích $S$ của hình phẳng giới hạn bởi đồ thị hàm số $y = f\left( x \right)$, trục hoành và hai đường thằng $x = a,x = b$ là: $S = \int\limits_a^b {\left| {f(x)} \right|dx} $
Phương trình hoành độ giao điểm của các đồ thị là: $\left\{ \begin{array}{l}2 - x = 0\\{x^3} = 0\\{x^3} = 2 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 2\\x = 0\\x = 1\end{array} \right.$
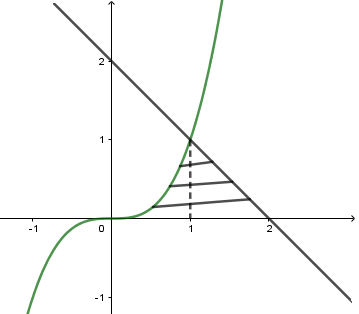
Nên diện tích hình phẳng cần tính là $S = \int\limits_0^1 {{x^3}dx + } \int\limits_1^2 {(2 - x)dx = } \dfrac{1}{2} + \int\limits_0^1 {{x^3}dx} $
Đáp án : C
Một số em sẽ chỉ giải phương trình ${x^3} = 2 - x$ được nghiệm \(x = 1\) và vội vàng kết luận \(S = \int\limits_0^1 {\left| {{x^3} + x - 2} \right|dx} \) là sai.








Danh sách bình luận