Cho tam giác ABC và M là trung điểm của đoạn thẳng BC.
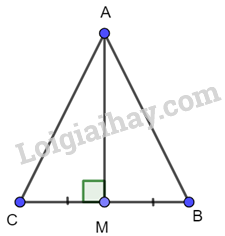
a) Giả sử AM vuông góc với BC. Chứng minh rằng tam giác ABC cân tại A.
b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rằng tam giác ABC cân tại A.
a) Chứng minh tam giác hai tam giác AMB và AMC bằng nhau \(\Rightarrow\) Tam giác ABC cân.
b) Từ M kẻ hai đường vuông góc với AC và AB từ đó chứng minh hai góc B và C bằng nhau.
\(\Rightarrow\) Chứng minh hai tam giác AMB và AMC bằng nhau
\(\Rightarrow\) Tam giác ABC cân
a)
Xét 2 tam giác vuông AMC và AMB có:
AM chung
BM=CM (gt)
=>\(\Delta AMC = \Delta AMB\) (hai cạnh góc vuông)
=> AC=AB (2 cạnh tương ứng)
=> Tam giác ABC cân tại A
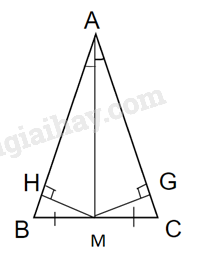
b)
Kẻ MH vuông góc với AB (H thuộc AB)
MG vuông góc với AC (G thuộc AC)
Xét 2 tam giác vuông AHM và AGM có:
AM chung
\(\widehat {HAM} = \widehat {GAM}\) (do AM là tia phân giác của góc BAC)
=>\(\Delta AHM = \Delta AGM\) (cạnh huyền – góc nhọn)
=> HM=GM (2 cạnh tương ứng)
Xét 2 tam giác vuông BHM và CGM có:
BM=CM (giả thiết)
MH=MG(chứng minh trên)
=>\(\Delta BHM = \Delta CGM\)(cạnh huyền – cạnh góc vuông)
=>\(\widehat {HBM} = \widehat {GCM}\)(2 góc tương ứng)
=>Tam giác ABC cân tại A.

Các bài tập cùng chuyên đề
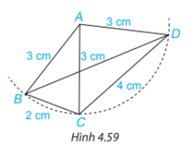
Hãy nêu tên tất cả các tam giác cân trong Hình 4.59. Với mỗi tam cân đó, hãy nêu tên cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của chúng.
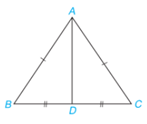
Quan sát tam giác ABC cân tại A như Hình 4.60. Lấy D là trung điểm của đoạn thẳng BC.
a) Chứng minh rằng \(\Delta \) ABD = \(\Delta \) ACD theo trường hợp cạnh - cạnh - cạnh.
b) Hai góc B và C của tam giác ABC có bằng nhau không?
Cho tam giác MNP có \(\widehat M = \widehat N\). Vẽ tia phân giác PK của tam giác \(MNP(K \in MN)\).
Chứng minh rằng:
a) \(\widehat {MKP} = \widehat {NKP}\);
b) \(\Delta MPK = \Delta NPK\);
c) Tam giác MNP có cân tại \(P\) không?
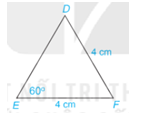
Tính số đo các góc và các cạnh chưa biết của tam giác DEF trong Hình 4.62.
Một tam giác có gì đặc biệt nếu thoả mãn một trong các điều kiện sau:
a) Tam giác có ba góc bằng nhau?
b) Tam giác cân có một góc bằng 60°?
Cho tam giác ABC cân tại A và M là trung điểm của đoạn thẳng BC. Chứng minh AM vuông góc với BC và AM là tia phân giác của góc BAC.
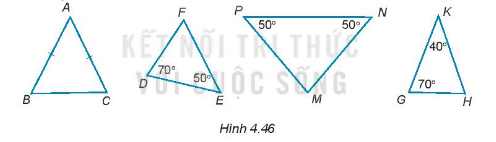
Trong những tam giác dưới đây (H.4.46), tam giác nào là tam giác cân, cân tại đỉnh nào? Vì sao?
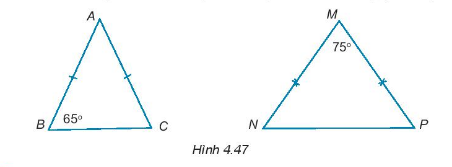
Tính số đo các góc còn lại trong các tam giác cân dưới đây (H.4.47)
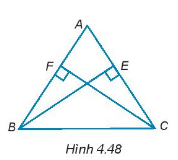
Tam giác ABC có 2 đường chéo BE và CF bằng nhau (H.4.48). Chứng minh rằng tam giác ABC cân tại đỉnh A.
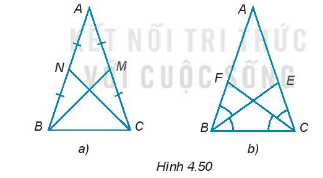
Cho ABC là tam giác cân tại đỉnh A. Chứng minh rằng:
a) Hai đường trung tuyến BM, CN bằng nhau (H.4.50a).
b) Hai đường phân giác BE, CF bằng nhau (H.4.50b)
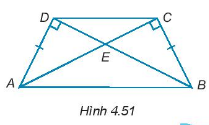
Cho các điểm A, B, C, D, E như Hình 4.51. Chứng minh rằng:
a) \(\Delta AEB,\Delta DEC\) là các tam giác cân đỉnh E.
b) \(AB\parallel CD.\)
Trong các câu sau đây, câu nào sai?
A. Tam giác tù là tam giác có một góc có số đo lớn hơn 90 độ.
B. Tam giác vuông là tam giác có một góc có số đo bằng 90 độ.
C. Tam giác cân là tam giác có ba góc có số đo bằng 60 độ.
D. Tam giác nhọn là tam giác có ba góc có số đo nhỏ hơn 90 độ
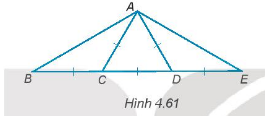
Cho Hình 4.61, hãy tính số đo các góc của tam giác ABE.
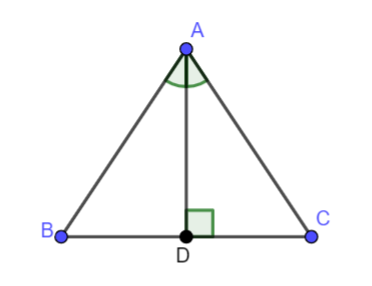
Cho tam giác ABC và M là trung điểm BC.
a) Giả sử AM vuông góc với BC. Chứng minh rẳng \(\Delta ABC\) cân tại A.
b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rẳng \(\Delta ABC\) cân tại A.
Cho tam giác ABC và điểm D nằm trên cạnh BC sao cho AD vuông góc với BC và AD là phân giác góc BAC. Chứng minh rằng \(\Delta ABC\)cân tại A.
Em hãy đo rồi so sánh độ dài hai cạnh AB và AC của tam giác ABC có trong hình di tích ga xe lửa Đà Lạt dưới đây.

Gấp đôi một tờ giấy hình chữ nhật ABCD theo đường gấp MS. Cắt hình gấp được theo đường chép AS rồi trải phẳng hình cắt được ra ta có tam giác SAB (Hình 1). Em hãy so sánh hai cạnh SA và SB của tam giác này.

Tìm các tam giác cân trong Hình 4. Kể tên các cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của mỗi tam giác cân đó.

Cho Hình 14, biết ED = EF và EI là tia phân giác của \(\widehat {DEF}\)
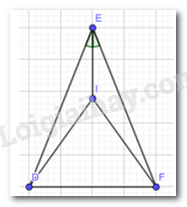
Chứng minh rằng:
a) \(\Delta EID = \Delta EIF\)
b) Tam giác DIF cân
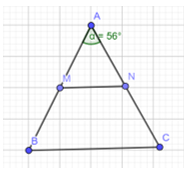
Cho tam giác ABC cân tại A có \(\widehat A = {56^o}\)(Hình 15)
a) Tính\(\widehat B\), \(\widehat C\)
b) Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng tam giác AMN cân.
c) Chứng minh rằng MN // BC
Cho tam giác ABC vuông tại A, vẽ đường cao AH. Trên tia đối của tia HA lấy điểm M sao cho H là trung điểm của AM.
a) Chứng minh rằng tam giác ABM cân.
b) Chứng minh rằng \(\Delta ABC = \Delta MBC\)
Cầu Long Biên bắc qua sông Hồng ở Thủ đô Hà Nội gợi nên hình ảnh tam giác ABC có sự đối xứng và cân bằng.

Tam giác ABC như vậy gọi là tam giác gì?
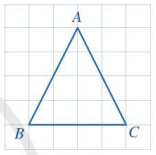
Trong Hình 69, hai cạnh AB và AC của tam giác ABC có bằng nhau hay không?
Một tam giác cân có góc ở đáy bằng 40° thì số đo góc ở đỉnh là
-
A.
50°;
-
B.
40°;
-
C.
140°;
-
D.
100°.
Cho tam giác ABC cân tại A, khẳng định nào sau đây SAI?
-
A.
AB = BC.
-
B.
AB = AC.
-
C.
\(\widehat B = \widehat C\).
-
D.
\(\widehat B = \frac{{180^\circ - \widehat A}}{2}\).
Cho \(\Delta ABC\) có AB = AC. Gọi I là trung điểm của BC.
a) Chứng minh \(\Delta ABI = \Delta ACI\) và \(AI \bot BC\).
b) Trên tia đối của tia IA lấy điểm K sao cho IA = IK. Chứng minh AB = KC.
c) Kẻ \(IE \bot AB\left( {E \in AB} \right)\), \(IF \bot KC\left( {F \in KC} \right)\). Chứng minh E, I, F thẳng hàng.
Cho tam giác MNP cân tại M. Kể tên các cạnh bên, cạnh đáy, góc ở đỉnh, góc ở đáy của tam giác cân đó.
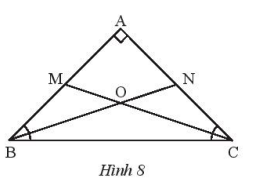
Cho tam giác ABC vuông cân tại A. Tia phân giác của góc B cắt AC tại N, tia phân giác của góc C cắt AB tại M. Gọi O là giao điểm của BN và CM.
a) Tính số đo các góc OBC, OCB.
b) Chứng minh rằng tam giác OBC cân.
c) Tính số đo góc BOC.
a) Tam giác có hai góc bằng \({60^o}\) có phải là tam giác hay không? Hãy tìm góc còn lại của tam giác này.
b) Tam giác có hai góc bằng \({45^o}\) có phải là tam giác cân hay không? Hãy tìm các góc còn lại của tam giác này.
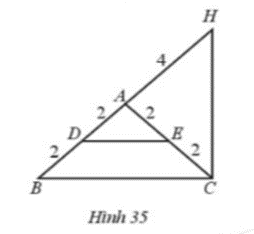
Tìm các tam giác cân trên Hình 35. Kể tên các cạnh bên, cạnh đáy, góc ở đáy, góc ở đỉnh của mỗi tam giác cân đó.







Danh sách bình luận