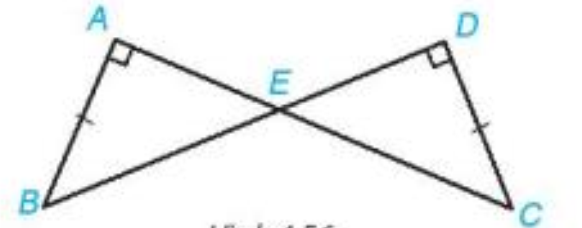
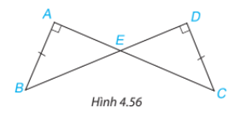
Cho hình 4.56, biết AB=CD, \(\widehat {BAC} = \widehat {BDC} = {90^o}\). Chứng minh rằng \(\Delta ABE = \Delta DCE\).
Chứng minh 2 tam giác vuông AEB và DEC bằng nhau theo trường hợp góc – cạnh - góc
Vì tổng 3 góc trong 1 tam giác luôn bằng 180 độ.
Xét hai tam giác AEB và DEC có:
\(\widehat {AEB} = \widehat {DEC}\)(đối đỉnh) và \(\widehat {BAC} = \widehat {BDC} = {90^o}\).
Suy ra: \(\widehat {ABE} = \widehat {DCE}\)
Xét 2 tam giác AEB và DEC có:
\(\widehat {BAC} = \widehat {BDC} (= {90^o}\))
\(AB=DC\) (gt)
\(\widehat {ABE} = \widehat {DCE}\) (cmt)
suy ra \(\Delta AEB = \Delta DEC\)(g.c.g)

Các bài tập cùng chuyên đề
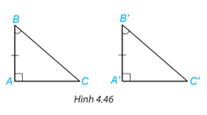
Hai tam giác vuông ABC (vuông tại đỉnh A) và A'B'C' (vuông tại đỉnh A') có tương ứng một cạnh góc vuông và một góc nhọn kề với cạnh ấy bằng nhau: AB = A'B', \(\widehat B = \widehat {B'}\) (H.4.46).
Dựa vào trường hợp bằng nhau góc - cạnh - góc của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và A'B'C' bằng nhau.
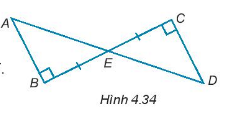
Cho các điểm A, B, C, D, E như H.4.34. Biết rằng E là trung điểm của BC, chứng minh rằng \(\Delta ABE = \Delta DCE\)
Biết rằng ABC và MNP là các tam giác vuông tại đỉnh A và M, AB = PM, \(\widehat C = \widehat N\). Câu nào dưới đây là đúng?
A. \(\Delta ABC = \Delta MPN\)
B. \(\Delta ABC = \Delta MNP\)
C. \(\Delta ABC = \Delta PMN\)
D. \(\Delta ABC = \Delta NMP\).
Cho các điểm A, B,C,D,E như hình bên. Chứng minh rằng \(\Delta ABE = \Delta DCE\).
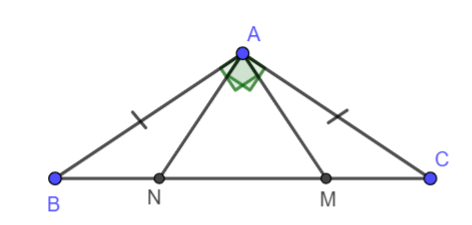
Cho tam giác ABC cân tại đỉnh A có \(\widehat A = {120^o}\). Trên cạnh BC lấy điểm M, N sao cho MA, NA lần lượt vuông góc AB, AC. Chứng minh rằng
a) \(\Delta BAM = \Delta CAN\)
b) Các tam giác ANB, AMC lần lượt cân tại N, M.
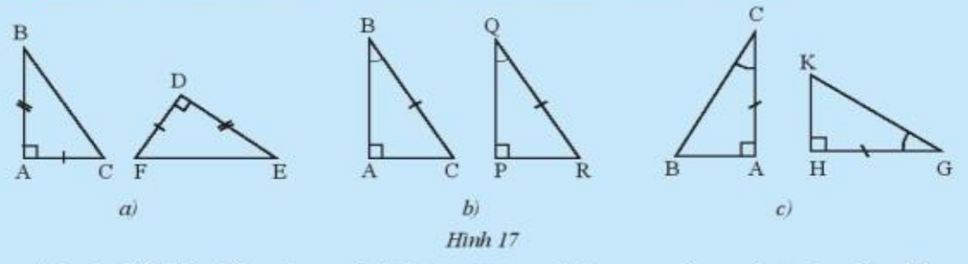
Hãy nêu các trường hợp bằng nhau cho mỗi cặp tam giác trong Hình 17. Từ các điều kiện bằng nhau của hai tam giác, người ta suy ra được các trường hợp bằng nhau sau đây của hai tam giác vuông.







Danh sách bình luận