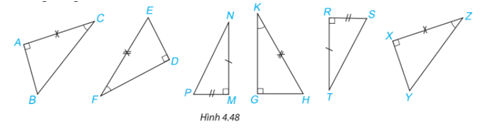
Trong Hình 4.48, hãy tìm các cặp tam giác vuông bằng nhau và giải thích vì sao chúng bằng nhau.
Chứng minh ba cặp tam giác vuông bằng nhau theo các trường hợp bằng nhau đã học.
+)Xét hai tam giác vuông ABC và XYZ có:
\(\widehat A = \widehat X( = 90^\circ )\) (gt)
AC=XZ (gt)
\(\widehat C = \widehat Z\) (gt)
\( \Rightarrow \Delta ABC = \Delta XYZ\) (g.c.g)
+)Xét hai tam giác vuông DEF và GHK có:
\(EF = HK\) (gt)
\(\widehat {EFD} = \widehat {GKH}\) (gt)
\( \Rightarrow \Delta DEF = \Delta GHK\) (cạnh huyền – góc nhọn)
+)Xét hai tam giác vuông MNP và RTS có:
\(MN = TR\) (gt)
\(\widehat R = \widehat M( = 90^\circ )\) (gt)
\(PM = SR\) (gt)
\( \Rightarrow \Delta MNP = \Delta RTS\) (c.g.c)
Các bài tập cùng chuyên đề
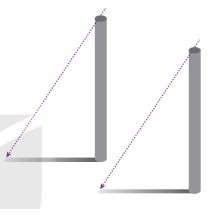
Quay lại tình huống mở đầu, ta thấy mỗi chiếc cột với bóng của nó tạo thành hai cạnh góc vuông của một tam giác vuông. Hai tam giác vuông này có hai cặp cạnh tương ứng bằng nhau và hai góc ở đỉnh chiếc cột của hai tam giác vuông này cũng bằng nhau. Vậy lí do mà bạn Tròn đưa ra có đúng không?
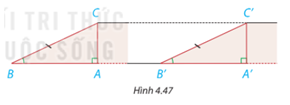
Hình 4.47 mô phỏng chiều dài và độ dốc của hai con dốc bởi các đường thẳng BC, B’C’ và các góc B, B’. Khi đó AC, A’C’ mô tả độ cao của hai con dốc.
a) Dựa vào trường hợp bằng nhau góc - cạnh - góc của hai tam giác, hãy giải thích vì sao hai tam giác vuông ABC và A’B’C’ bằng nhau.
b) So sánh độ cao của hai con dốc.
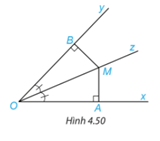
Cho Oz là tia phân giác của góc xOy. Lấy điểm M trên tia Oz và hai điểm A, B lần lượt trên các tia Ox, Oy sao cho MA vuông góc với Ox, MB vuông góc với Oy(H.4.50). Chứng minh rằng MA = MB.
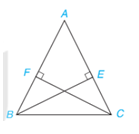
Cho tam giác ABC cân tại A và các điểm E, F lần lượt nằm trên các cạnh AC, AB sao cho BE vuông góc với AC, CF vuông góc với AB (H.4.69). Chứng minh rằng BE = CF.
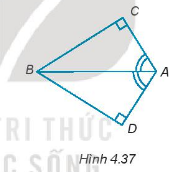
Cho 4 điểm A, B, C, D như Hình 4.37. Biết rằng \(\widehat {DAB} = \widehat {CAB}\), hãy chứng minh CB = DB.
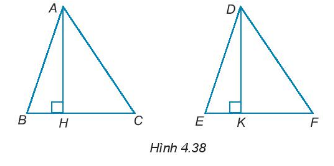
Cho AH và DK lần lượt là hai đường cao của hai tam giác ABC và DEF như Hình 4.38. Biết rằng \(\Delta ABC = \Delta DEF\). Hãy chứng minh AH = DK.
Biết rằng ABC và MNP là các tam giác vuông tại đỉnh A, M và BC = PN, \(\widehat C = {50^o},\widehat P = {40^o}\). Câu nào dưới đây là đúng?
A. \(\Delta ABC = \Delta MPN\)
B. \(\Delta ABC = \Delta MNP\)
C. AB = MN
D. AC = MP.
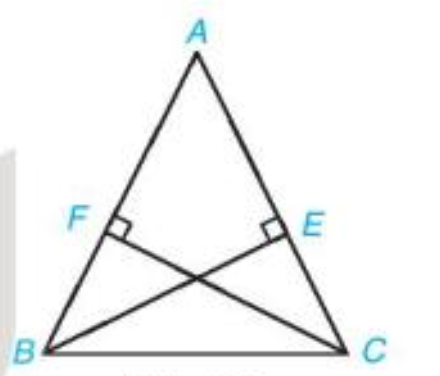
Cho tam giác ABC cân tại A. Chứng minh rằng hai đường cao BE và CF bằng nhau.
Cho góc \(xOy\) khác góc bẹt có \(Ot\) là tia phân giác. Qua điểm \(H\) thuộc tia \(Ot\), kẻ đường vuông góc với \(Ot\) và cắt \(Ox\) và \(Oy\) theo thứ tự \(A\) và \(B\).
Chứng minh \(OA = OB.\)
Cho tam giác ABC có M là trung điểm cạnh BC. Kẻ tia Ax đi qua M. Qua B, C lần lượt kẻ các đường thẳng vuông góc với Ax, cắt Ax tại H và K. So sánh BH và CK.
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối tia của tia CB lấy điểm N sao cho BM = CN. Kẻ BE ⊥ AM (E ∈ AM), CF ⊥ AN (F ∈ AN).
Chứng minh rằng ∆BME = ∆CNF.
