- Cho hình bình hành \(ABCD\) có \(AB = AD\). Giải thích vì sao bốn cạnh của \(ABCD\) bằng nhau? Khi đó tứ giác \(ABCD\) là hình gì?
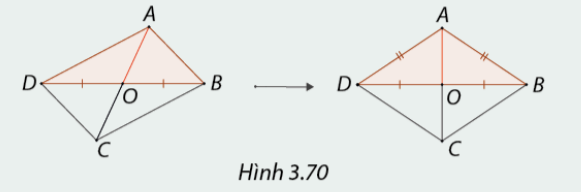
- Cho hình bình hành \(ABCD\) như Hình 3.70. Dựa vào dấu hiệu của tam giác cân, hãy bổ sung một điều kiện cho trung tuyến \(AO\) để tam giác \(ABD\) cân tại \(A\). Khi đó tứ giác \(ABCD\) là hình gì?
Dựa vào định nghĩa và tính chất của hình thoi để chứng minh.
- Hình bình hành \(ABCD\) có \(AB = AD\)
Mà theo tính chất của hình bình hành thì các cạnh đối diện bằng nhau
→ \(AB = DC = AD = BC\)
Vì hình bình hành \(ABCD\) có bốn cạnh bằng nhau nên \(ABCD\) cũng là hình thoi.
- Để tam giác \(ABD\) cân tại \(A\) thì trung tuyến \(AO\) phải vuông góc với \(BD\).
Khi đó tứ giác \(ABCD\) là hình thoi vì có hai đường chéo \(AC \bot BD\) và chúng cắt nhau tại trung điểm của mỗi đường.

Các bài tập cùng chuyên đề
Một hoa văn trang trí được ghép bởi ba hình tứ giác có độ dài mỗi cạnh đều bằng 2cm (hình 18). Gọi tên các tứ giác này và tính chu vi của hoa văn.

Một tứ giác có chu vi là \(52\) cm và một đường chéo là \(24\)cm. Tính độ dài của mỗi cạnh và đường chéo còn lại nếu biết hai đường chéo vuông góc tại trung điểm của mỗi đường.
Cho tam giác \(ABC\) cân tại \(A\), gọi \(M\) là trung điểm của \(BC\). Lấy điểm \(D\) đối xứng với điểm \(A\) qua \(BC\).
a) Chứng minh tứ giác \(ABDC\) là hình thoi
b) Gọi \(E\), \(F\) lần lượt là trung điểm của \(AB\) và \(AC\), lấy điểm \(O\) sao cho \(E\) là trung điểm của \(OM\). Chứng minh rằng hai tam giác \(AOB\) và \(MBO\) bằng nhau
c) Chứng minh tứ giác \(AEMF\) là hình thoi
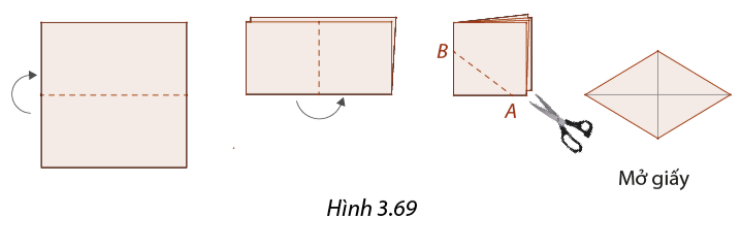
Gấp một tờ giấy làm tư như Hình 3.69 và cắt chéo theo đường \(AB\) bất kì (\(A,B\) nằm trên hai mép gấp). Sau khi mở giấy, tứ giác cắt được là hình gì? Vì sao?
Cho hình chữ nhật \(ABCD\) và \(M,N,P,Q\) lần lượt là trung điểm các cạnh \(AB,BC,CD,AD\). Chứng minh rằng \(MNPQ\) là hình thoi.
Hàng rào được đóng từ các thanh gỗ thẳng như trong Hình 3.75 với các thanh \(BN,BQ,DM,DP\) đều bằng 1,3 cm và thanh \(BD\) dài 0,5 cm. Điểm A là trung điểm chung của hai thành \(BN\)và \(DM\), điểm \(C\) là trung điểm chung của hai thanh \(BQ\) và \(DP\).
a) Chứng minh rằng tứ giác \(ABCD\) là hình thoi.
b) Tính khoảng cách giữa hai điểm A và C.

Cho hình bình hành ABCD có \(AD = 2AB\). Gọi M là trung điểm của AD. Kẻ CE vuông góc với AB tại E, MF vuông góc với CE tại F, MF cắt BC tại N. Chứng minh rằng:
a) Tứ giác MDCN là hình thoi;
b) Tam giác EMC là tam giác cân;
c) \(\widehat {BAD} = 2\widehat {AEM}\).
Điền cụm từ thích hợp vào chỗ trống
a) Trong hình thoi ............................ vuông góc với nhau và là ............................................ các góc của hình thoi.
b) Hình bình hành ....................................... bằng nhau là hình thoi.
c) Hình bình hành có ............. đường chéo .............................. với nhau là hình thoi.
d) Tứ giác có ............. cặp cạnh đối ...................................... và có một đường chéo ..................... của một góc là hình thoi.
Cho tam giác ABC nhọn có \(AB < AC\). Gọi \(N\) là trung điểm của \(AC\). Lấy điểm \(D\) trên tia \(BN\) sao cho \(BN = ND\). Kẻ \(AP \bot BC\), \(CQ \bot AD\).
a) Chứng minh \(N\) là trung điểm của \(PQ\).
b) Tam giác \(ABC\) cần thêm điều kiện gì để tứ giác \(ABCD\) là hình vuông.







Danh sách bình luận