Một con lắc đơn lớn được treo ở sảnh của tòa nhà Liên Hợp Quốc tại thành phố New York, Mỹ. Quả cầu có khối lượng 91 kg và sợi dây treo dài 22,9 m. Con lắc liên tục dao động với chu kì 9,6 s.

Khi con lắc đơn dao động, nó có những dạng năng lượng nào?

Dựa vào công thức (3.5) và Hình 3.3, mô tả sự thay đổi của động năng trong một chu kì dao động của vật.

So sánh pha dao động của thế năng và động năng khi vật dao động điều hòa.

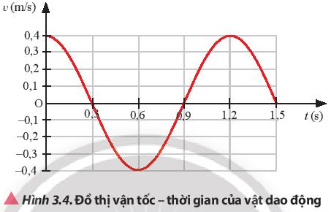
Một vật có khối lượng 2 kg dao động điều hoà có đồ thị vận tốc – thời gian như Hình 3.4. Xác định tốc độ cực đại và động năng cực đại của vật trong quá trình dao động.

Một vật dao động điều hoà có phương trình li độ là x=5cos(10t) (x tính bằng cm, t tính bằng s). Động năng và thế năng biến thiên tuần hoàn với tần số góc bằng bao nhiêu?

A. 10 rad/s.

B. 10t rad/s.

C. 5 rad/s.

D. 20 rad/s.

Một con lắc lò xo gồm vật nặng có khối lượng 0,2 kg gắn vào một lò xo. Kích thích cho con lắc dao động với biên độ 6 cm và tần số góc 5 rad/s. Tính động năng của chất điểm khi nó đi qua vị trí có li độ 2 cm.

Phương trình dao động của một chất điểm dao động điều hoà là:

\(x = A\cos \left( {\omega t + \frac{{2\pi }}{3}} \right)(cm)\)

Động năng của nó biến thiên theo thời gian theo

A. \({W_d} = \frac{{m.{A^2}.{\omega ^2}}}{4}\left[ {1 + \cos \left( {2\omega t + \frac{\pi }{3}} \right)} \right]\)

B. \({W_d} = \frac{{m.{A^2}.{\omega ^2}}}{4}\left[ {1 - \cos \left( {2\omega t + \frac{{4\pi }}{3}} \right)} \right]\)

C. \({W_d} = \frac{{m.{A^2}.{\omega ^2}}}{2}\left[ {1 + \cos \left( {2\omega t + \frac{{4\pi }}{3}} \right)} \right]\)

D. \({W_d} = \frac{{m.{A^2}.{\omega ^2}}}{4}\left[ {1 + \cos \left( {2\omega t + \frac{{4\pi }}{3}} \right)} \right]\)  

Một chất điểm dao động điều hoà. Biết khoảng thời gian giữa năm lần liên tiếp động năng của chất điểm bằng thế năng của hệ là 0,4 s. Tần số của dao động là

A. 2,5 Hz.                  

B. 3,125 Hz.              

C. 5 Hz.                  

D. 6,25 Hz.

Một chất điểm có khối lượng m, dao động điều hoà với biên độ A, tần số góc \(\omega \). Động năng cực đại của chất điểm là

A. \(\frac{{m.{A^2}.{\omega ^2}}}{2}\)           

B. \(\frac{{{A^2}.{\omega ^2}}}{{2m}}\)               

C. \(\frac{{m.A.{\omega ^2}}}{2}\)                  

D. \(\frac{{m.{A^2}.\omega }}{2}\)

Một chất điểm có khối lượng 100 g dao động điều hoà trên quỹ đạo là đoạn thẳng MN (dài hơn 8 cm). Tại điểm P cách M 4 cm và tại điểm Q cách N 2 cm chất điểm có động năng tương ứng là \({32.10^{ - 3}}\) J và \({18.10^{ - 3}}\)J. Tính tốc độ trung bình khi vật đi từ M đến N.

Một vật nhỏ khối lượng 0,10 kg dao động điều hoà theo phương trình x = 8,0cos10,0t (x tính bằng cm; t tính bằng s). Động năng cực đại của vật là

A. 32 mJ.

B. 16 mJ.

C. 64 mJ.

D. 28 mJ.

Một con lắc lò xo gồm vật có khối lượng 0,500 kg gắn vào đầu tự do của một lò xo nhẹ có độ cứng 20,0 N/m. Con lắc dao động theo phương nằm ngang với biên độ 4,00 cm.

a) Tính tốc độ cực đại của vật dao động.

b) Tính cơ năng dao động của con lắc.

c) Tính động năng và tốc độ của vật khi nó ở vị trí có li độ 2,00 cm.

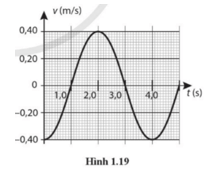
Hình 1.19 là đồ thị vận tốc – thời gian của một con lắc đơn dao động điều hoà với cơ năng 9,6 mJ. Hãy xác định:

a) Khối lượng của vật nhỏ.

b) Biên độ của dao động.

c) Li độ của con lắc tại thời điểm 1,5 s.