Pít-tông bên trong động cơ ô tô dao động lên và xuống khi động cơ ô tô hoạt động (Hình 2.6). Các dao động này được coi là dao động điều hòa với phương trình li độ của pít-tông là \(x = 12,5\cos (60\pi t)\). Trong đó, x tính bằng cm, t tính bằng s. Xác định:
a. Biên độ, tần số và chu kì của dao động.
b. Vận tốc cực đại của pít-tông.
c. Gia tốc cực đại của pít-tông.
d. Li độ, vận tốc, gia tốc của pít-tông tại thời điểm t = 1,25s

Từ phương trình li độ có dạng: \(x = A\cos (\omega t + \varphi )\), suy ra các đại lượng: biên độ A, tần số góc \(\omega \). Sử dụng các công thức liên hệ giữa các đại lượng để tìm ra đại lượng mà đề bài yêu cầu.
Phương trình li độ của pít-tông là \(x = A\cos (\omega t + \varphi )\)(cm).
a. Ta có: Biên độ của dao động là: A = 12,5 cm = 0,125 m. Tần số góc \(\omega = 60\pi \)(rad/s).
Tần số của dao động là: \(f = \frac{\omega }{{2\pi }} = \frac{{60\pi }}{{2\pi }} = 30\)(Hz).
Chu kì của dao động là: \(f = \frac{1}{T} = \frac{1}{{30}} \approx 0,033\)(s).
b. Vận tốc cực đại của pít-tông là: \({v_{\max }} = \omega A = 60\pi .0,125 \approx 23,562\)(m/s).
c. Gia tốc cực đại của pít-tông là: \({a_{\max }} = {\omega ^2}A = {(60\pi )^2}.0,125 \approx 4441,3\)(m/s2).
d. Tại thời điểm t = 1,25 s, li độ của vật là:
\(x = 12,5\cos (60\pi t) = 12,5\cos (60\pi .1,25) = - 12,5\)(cm).
Lúc này vật đang ở vị trí biên âm nên vận tốc v = 0.
Gia tốc của vật là: \(a = - {\omega ^2}x = - {(60\pi )^2}.( - 0,125) \approx 4441,3\)(m/s2).

Các bài tập cùng chuyên đề
Một vật dao động điều hoà có phương trình \({\rm{x}} = 2\cos \left( {4\pi {\rm{t}} + \frac{\pi }{2}} \right)({\rm{cm}})\)
Hãy xác định:
a) Biên độ và pha ban đầu của dao động.
b) Pha và li độ của dao động khi \(t = 2\left( s \right)\)
Ta có thể dựa vào đồ thị (x – t) của dao động điều hòa để xác định vận tốc và gia tốc của vật được không?
1. Một vật dao động điều hoà trên trục Ox. Khi vật qua vị trí cân bằng thì tốc độ của nó là 20 cm/s. Khi vật có tốc độ là 10 cm/s thì gia tốc của nó có độ lớn là \(40\sqrt 3 \)cm/s2. Tính biên độ dao động của vật
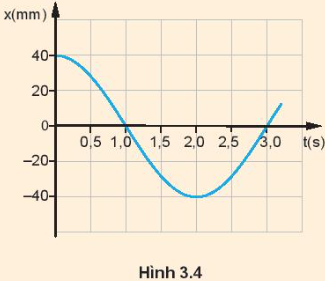
2. Hình 3.4 là đồ thị li độ – thời gian của một vật dao động điều hoà. Sử dụng đô thị để tính các đại lượng sau:
a) Tốc độ của vật ở thời điểm t=0 s.
b) Tốc độ cực đại của vật.
c) Gia tốc của vật tại thời điểm t = 1,0 s
Khi biết phương trình hoặc đồ thị của vật dao động điều hoà, làm thế nào để xác định được vận tốc và gia tốc của vật?
1. Nếu đề bài cho phương trình dao động không đúng dạng cơ bản x=Acos(ωt+φ) thì ta xác định pha ban đầu như thế nào?
2. Có thể sử dụng mối liên hệ giữa dao động điều hoà và chuyển động tròn đều để xác định pha ban đầu, thời gian để vật đi từ điểm này đến điểm khác trong dao động điều hoà được không?
Một vật dao động điều hoà có phương trình là x = 2 cos(4πω −\(\frac{\pi }{6}\)) (cm). Hãy cho biết biên độ, tần số góc, chu kì, tần số, pha ban đầu và pha của dao động ở thời điểm t = 1s.
Một vật dao động điều hoà dọc theo trục Ox, quanh điểm gốc 0, với biên độ A = 10 cm và chu kì T = 2 s. Tại thời điểm t= 0,vật có li độ x = A.
a) Viết phương trình dao động của vật.
b) Xác định thời điểm đầu tiên vật qua vị trí có li độ x = 5 cm.
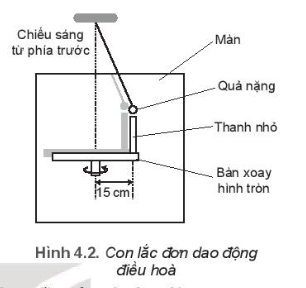
Hình 4.2 là sơ đồ của một bàn xoay hình tròn, có gắn một thành nhỏ cách tâm bàn 15 cm. Bàn xoay được chiếu sáng bằng nguồn sáng rộng, song song, hướng chiếu sáng từ phía trước màn để bóng đổ lên màn hình. Một con lắc đơn dao động điều hoà phía sau bàn xoay với biên độ bằng khoảng cách từ thanh nhỏ đến tâm bàn xoay. Tốc độ quay của bàn quay được điều chỉnh là 2π rad/s. Bóng của thanh nhỏ và quả nặng của con lắc luôn trùng nhau.
a) Tại sao nói dao động của bóng của thanh nhỏ và quả nặng là đồng pha?
b) Viết phương trình dao động của con lắc. Chọn gốc thời gian là lúc con lắc ở vị trí hiển thị trong Hình 4.2
c) Bàn xoay đi một góc 60° tử vị trí ban đầu, tính li độ của con lắc và tốc độ của nó tại thời điểm này.
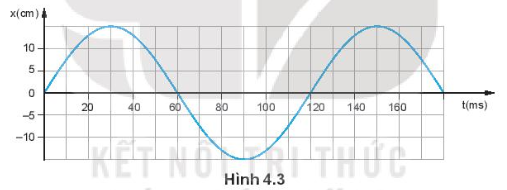
Hình 4.3 là đồ thị li độ – thời gian của một vật dao động điều hoà.
a) Xác định biên độ, chu kì, tần số, tần số góc và pha ban đầu của vật dao động.
b) Viết phương trình dao động của vật
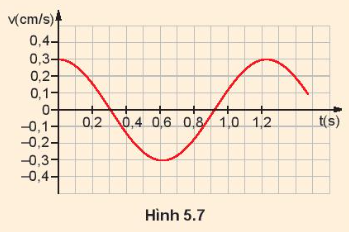
1. Một con lắc lò xo có vật nặng khối lượng 0,4 kg, dao động điều hòa. Đồ thị vận tốc v theo thời gian t như hình 5.7. Tính:
a) Vận tốc cực đại của vật.
b) Động năng cực đại của vật.
c) Thế năng cực đại của con lắc.
d) Độ cứng k của lò xo.
2. Một con lắc lò xo có độ cứng k = 100 N/m, vật nặng có khối lượng m = 200 g, dao động điều hòa với biên độ A = 5 cm.
a) Xác định li độ của vật tại thời điểm động năng của vật bằng 3 lần thế năng của con lắc.
b) Xác định tốc độ của vật khi qua vị trí cân bằng.
c) Xác định thế năng của con lắc khi vật có li độ x = -2,5 cm
Hãy chứng minh rằng khi góc lệch α nhỏ (sinα ≈ α rad) thì công thức (5.6) trở thành công thức (5.7)
Việc nghiên cứu các quả trình dao động điều hoà để ứng dụng vào thực tiễn như xây dựng mô hình dự báo động đất yêu cầu ta phải mô tả chính xác trạng thái của vật dao động tại những thời điểm xác định. Ngoài ra, dao động điều hoà có tính chất tuần hoàn theo thời gian và bị giới hạn trong không gian thì phương trình li độ, vận tốc và gia tốc của vật dao động điều hoà có những khác biệt gì so với chuyển động thẳng đều và biến đổi đều mà em đã học ở chương trình Vật lí 10?
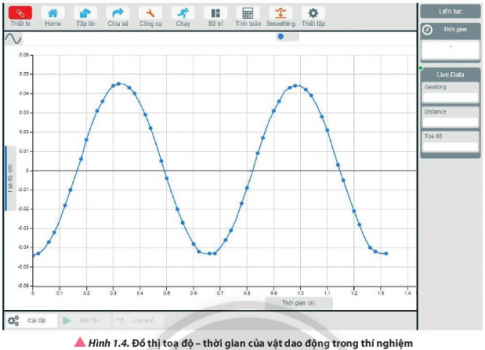
Quan sát dao động của con lắc lò xo và kết hợp với Hình 1.4, hãy chỉ rõ sự khác nhau giữa hình dạng quỹ đạo chuyển động và đồ thị li độ của vật dao động theo thời gian.
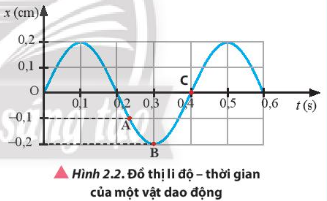
Một vật dao động có đồ thị li độ – thời gian được mô tả trong Hình 2.2. Hãy xác định:
a) Biên độ dao động, chu kì, tần số, tần số góc của dao động.
b) Li độ của vật dao động tại các thời điểm t1, t2, t3 ứng với các điểm A, B, C trên đường đồ thị li độ – thời gian.
c) Độ dịch chuyển so với vị trí ban đầu tại thời điểm t1, t2, t3 trên đường đồ thị.
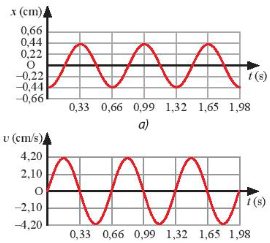
Quan sát Hình 2.3a và 2.3b, hãy xác định:
a) Hình dạng đồ thị vận tốc – thời gian của vật.
b) Chu kì của vận tốc của vật.
c) Mối liên hệ giữa tốc độ cực đại và biên độ của vật.
d) Độ lệch pha của vận tốc so với li độ của vật.
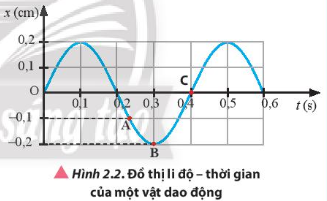
Hãy vẽ phác đồ thị lực tác dụng - thời gian của vật dao động điều hoà có đồ thị li độ – thời gian như Hình 2.2.
Dựa vào các đồ thị trong Hình 2.3:
a) Viết phương trình li độ, vận tốc và gia tốc của vật dao động điều hòa.
b) Mô tả định tính tính chất của li độ, vận tốc và gia tốc của vật tại các thười điểm 0,33 s; 0,495s và 0,66 s
c) Dựa vào các phương trình được xây dựng ở câu a để kiểm chứng lại mô tả định tính ở câu b
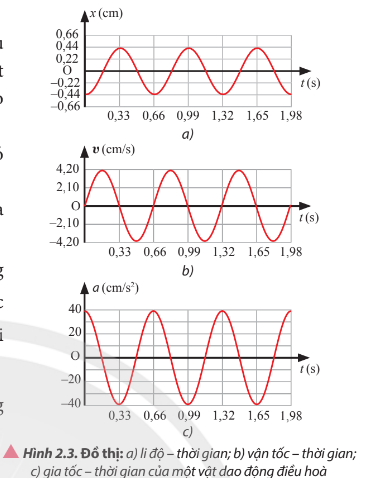
Nhận xét về độ lệch pha giữa gia tốc và vận tốc của vật dao động.
Một máy cơ khí khi hoạt động sẽ tạo ra những dao động được xem gần đúng là dao động điều hoà với phương trình li độ có dạng:
x=2cos(180πt) (mm)
a) Hãy xác định biên độ, chu kì, tần số và tần số góc của dao động.
b) Viết phương trình vận tốc và gia tốc của vật dao động.
Một chất điểm dao động điều hoà với biên độ 4 cm, tần số 1 Hz. Tại thời điểm ban đầu, vật ở vị trí biên âm. Hãy xác định vận tốc và gia tốc của vật tại thời điểm t = 1s.
Một vật thực hiện dao động điều hoà có li độ phụ thuộc vào thời gian theo biểu thức
A. \(x = A{t^2}\)
B. \(x = A\cos (\omega t + {\varphi _0})\)
C. \(x = {v_0}t\)
D. \(x = {v_0}t + \frac{1}{2}a{t^2}\)
Một chất điểm dao động điều hoà với phương trình li độ \(x = 3\cos (2\pi t + \frac{\pi }{4})\) (cm). Pha ban đầu của dao động trên là
A. 3 rad
B. 2π rad
C. \(\frac{\pi }{4}\) rad
D. \((2\pi t + \frac{\pi }{4})\) rad
Quãng đường một vật đi được trong một chu kì dao động điều hoà là 24 cm. Biên độ dao động của vật là
A. 24cm
B. 12 cm
C. 6cm
D. 8cm
Trong dao động điều hoà, vận tốc và gia tốc biến thiên điều hoà theo thời gian và có cùng
A. biên độ.
B. tần số
C. pha ban đầu
D. pha
Một vật cho động điều hoà theo một trục cố định. Phát biểu nào dưới đây là không chính xác
A. Quãng đường vật đi được trong một chu kì dao động bằng 4 lần biên độ
B. Đồ thị li độ theo thời gian của vật là một đường hình sin
C. Chiều dài quỹ đạo chuyển động của vật bằng 2 lần biên độ
D. Quỹ đạo chuyển động của vật là một đường hình sin
Một chất điểm dao động điều hoà trên trục Ox có phương trình li độ \(x = 8\cos (\pi t + \frac{\pi }{a})\) ( x tính bằng cm, t tính bằng s) thì:
(1) lúc t=0 s, chất điểm chuyển động theo chiều âm của trục Ox.
(2) chất điểm chuyển động trên đoạn thẳng dài 16 cm.
(3) chu kì dao động là 4 s.
(4) vận tốc chất điểm khi qua vị trí cân bằng là 8 cm/s.
(5) gia tốc của chất điểm cực đại tại vị trí x = 8 cm.
Trong các phát biểu trên, số phát biểu đúng là
A. 1
B. 2
C. 3
D. 4
Trong dao động điều hoà, phát biểu nào dưới đây là không chính xác
(1) Ở vị trí biên âm, gia tốc có giá trị cực tiểu, vận tốc bằng 0.
(2) Ở vị trí biên âm, gia tốc có giá trị cực đại, vận tốc bằng 0.
(3) Ở vị trí cân bằng, gia tốc có giá trị cực đại, vận tốc bằng 0.
(4) Ở vị trí cân bằng, gia tốc bằng 0, vận tốc có độ lớn cực đại.
(5) Ở vị trí biên dương, gia tốc có giá trị cực tiểu, vận tốc bằng 0.
(6) Ở vị trí biên dương, gia tốc có giá trị cực đại, vận tốc bằng 0.
A. (1), (3), (6).
B. (2), (5), (6).
C. (2), (4), (5).
D. (3), (4), (5).
Một vật dao động điều hoà có đô thị li độ – thời gian như Hình 2.1. Tại thời điểm t = 0,5 s, vận tốc của vật có độ lớn là
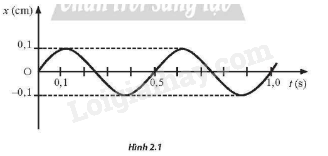
A. \(\frac{\pi }{5}cm/s\)
B. \(\frac{{2\pi }}{5}cm/s\)
C. \(\frac{{3\pi }}{5}cm/s\)
D. \(\frac{{4\pi }}{5}cm/s\)
Một chất điểm dao động điều hoà với phương trình vận tốc \(v = 2\sqrt 2 \cos (2t + \frac{{2\pi }}{5})\) (cm/s). Tại thời điểm vật có vận tốc tức thời là 2 cm/s thi li độ của vật có thể là
A. 1 cm.
B. \(\sqrt 2 \) cm.
C. 2 cm.
D. \(2\sqrt 2 \)cm.
Một chất điểm dao động điều hoà trên trục Ox, gốc toạ độ O tại vị trí cân bằng. Biết phương trình vận tốc của chất điểm là: \(v = 10\pi \cos \left( {\pi t + \frac{{5\pi }}{6}} \right)cm/s\). Phương trình li độ của chất điểm có dạng là
A. \(x = 10\cos \left( {\pi t + \frac{\pi }{3}} \right)\)cm
B. \(x = 10\cos \left( {\pi t - \frac{\pi }{3}} \right)\)cm
C. \(x = 10\cos \left( {\pi t + \frac{{5\pi }}{6}} \right)\)cm
D. \(x = 10\cos \left( {\pi t + \frac{{4\pi }}{3}} \right)\)cm







Danh sách bình luận