Một hình chữ nhật có diện tích là \(6{x^2} + 7x + 2\) (\(c{m^2}\)) và độ dài một cạnh là \(3x + 2\) (\(cm\)). Viết phân thức theo \(x\) biểu diễn độ dài cạnh còn lại và rút gọn phân thức này.

Rút gọn các phân thức sau:

a) \(\dfrac{{3{x^2} + 6xy}}{{6{x^2}}}\)                                          

b) \(\dfrac{{2{x^2} - {x^3}}}{{{x^2} - 4}}\)                                        

c) \(\dfrac{{x + 1}}{{{x^3} + 1}}\)

Mỗi cặp phân thức sau có bằng nhau không? Tại sao?

a) \(\dfrac{{3ac}}{{{a^3}b}}\) và \(\dfrac{{6c}}{{2{a^2}b}}\)

b) \(\dfrac{{3ab - 3{b^2}}}{{6{b^2}}}\) và \(\dfrac{{a - b}}{{2b}}\) 

Rút gọn các phân thức sau:

a) \(\dfrac{{3{x^2}y}}{{2x{y^5}}}\)

b) \(\dfrac{{3{x^2} - 3x}}{{x - 1}}\) 

c) \(\dfrac{{a{b^2} - {a^2}b}}{{2{a^2} + a}}\)

d) \(\dfrac{{12\left( {{x^4} - 1} \right)}}{{18\left( {{x^2} - 1} \right)}}\)

Cho phân thức: \(\dfrac{{4{{\rm{x}}^2}y}}{{6{\rm{x}}{y^2}}}\)

a) Tìm nhân tử chung của tử và mẫu

b) Tìm phân thức nhận được sau khi chia cả tử và mẫu cho nhân tử chung đó.

Rút gọn mỗi phân thức sau:

\(a)\dfrac{{8{{\rm{x}}^2} + 4{\rm{x}}}}{{1 - 4{{\rm{x}}^2}}}\)                                                    \(b)\dfrac{{{x^3} - x{y^2}}}{{2{{\rm{x}}^2} + 2{\rm{x}}y}}\)

Rút gọn mỗi phân thức sau:

\(a)\dfrac{{24{{\rm{x}}^2}{y^2}}}{{16{\rm{x}}{y^3}}}\)                                             

\(b)\dfrac{{6{\rm{x}} - 2y}}{{9{{\rm{x}}^2} - {y^2}}}\)

Rút gọn phân thức \(\frac{{{a^2}b - {a^2}}}{{{a^3} - {a^3}b}}\). Từ đó, tính giá trị của phân thức tại \(a = 0,5\).

Tìm đa thức thích hợp cho mỗi ô ?:

a)     \(\frac{{{x^2} - x}}{{\left( {x - 1} \right)\left( {x + 3} \right)}} = \frac{?}{{x + 3}}\)

b)    \(\frac{{x + y}}{?} = \frac{{{x^2} + 2xy + {y^2}}}{{7\left( {{x^2} - {y^2}} \right)}}\)

Rút gọn các phân thức sau:

a)     \(\frac{{4{x^4}{y^3}{z^2}}}{{12{x^2}{y^4}{z^3}}}\)

b)    \(\frac{{25x{y^3}\left( {x - y} \right)}}{{15{x^2}y{{\left( {x - y} \right)}^4}}}\)

c)     \(\frac{{xy - 2x}}{{2{x^2} - {x^2}y}}\)

d)    \(\frac{{{x^2} + xy - x - y}}{{{x^2} - xy - x + y}}\)

Một chiếc du thuyền chạy xuôi dòng từ điểm xuất phát A đến điểm tham quan B với tốc độ trung bình là \({v_1}\) (km/h). Sau đó thuyền chạy ngược dòng từ B trở về A với tốc độ trung bình là \(v{ _2}\) (km/h). Khi đó tốc độ trung bình \(v\) cho toàn bộ hành trình được xác định bởi

\(v = \frac{{2{v_1}{v_2}}}{{{v_1} + {v_2}}}\)

Chứng minh rằng nếu \({v_1} = 2{v_2}\) thì \(v = \frac{{4{v_2}}}{3}\).

Rút gọn các phân thức sau:

a)     \(\frac{{24{a^5}{b^3}}}{{18{a^3}{b^4}}}\)

b)    \(\frac{{2x - {x^2}}}{{{x^2}y - 4y}}\)

c)     \(\frac{{12{x^2} + 28x + 8}}{{9{x^2} - 1}}\)

d)    \(\frac{{{x^3} + {x^2} + x + 1}}{{{x^2} - 1}}\)

Rút gọn các phân thức sau:

a) \(\frac{{6ab}}{{ - 4ac}}\);

b) \(\frac{{ - {a^4}b}}{{ - 2{a^2}{b^3}}}\);

c) \(\frac{{5a\left( {a - b} \right)}}{{10b\left( {b - a} \right)}}\);

d) \(\frac{{3a\left( {1 - a} \right)}}{{9{{\left( {a - 1} \right)}^2}}}\).

Rút gọn các phân thức sau:

a) \(\frac{{3x + 3y}}{{6xy}}\);

b) \(\frac{{3x - 6y}}{{12y - 6x}}\);

c) \(\frac{{6{x^2} - 18xy}}{{12{x^2} - 6xy}}\);

d) \(\frac{{{x^3} + 3{x^2}y}}{{{x^2}y + 3{x^3}}}\).

Rút gọn các phân thức sau:

a) \(\frac{{5y - xy}}{{{x^2} - 25}}\);          

b) \(\frac{{9 + 6x + {x^2}}}{{3x + 9}}\)               

c) \(\frac{{2{x^3}y + 2x{y^3}}}{{{x^4} - {y^4}}}\)

d) \(\frac{{2 - 4x}}{{4{x^2} - 4x + 1}}\)     

e) \(\frac{{x - 2}}{{{x^3} - 8}}\)                           

g) \(\frac{{{x^4}{y^2} - {x^2}{y^4}}}{{{x^2}\left( {x + y} \right)}}\)

Rút gọn mỗi phân thức sau:

a) \(\frac{{25{x^2}{y^3}}}{{35{x^3}{y^2}}}\)

b) \(\frac{{x - y}}{{y - x}}\)

c) \(\frac{{{{\left( { - x} \right)}^5}{y^2}}}{{{x^2}{{\left( { - y} \right)}^3}}}\)

d) \(\frac{{{x^2} - 2x}}{{{x^3} - 4{x^2} + 4x}}\)

Chứng tỏ giá trị của biểu thức sau không phụ thuộc vào giá trị của biến (với \(a\) là một số):

a) \(\frac{{{x^2} - {y^2}}}{{\left( {x + y} \right)\left( {ax - ay} \right)}}\left( {a \ne 0} \right)\)

b) \(\frac{{{{\left( {x + a} \right)}^2} - {x^2}}}{{2x + a}}\)

Rút gọn rồi tính giá trị biểu thức:

a) \(A = x + 1 - \frac{{{x^2} - 4}}{{x - 1}}\) tại \(x =  - 4\)

b) \(B = \frac{1}{{5 - x}} - \frac{{{x^2} + 5x}}{{{x^2} - 25}}\) tại \(x = 99\)

c) \(C = \frac{1}{{x - 1}} - \frac{{2x}}{{{x^3} - {x^2} + x - 1}}\) tại \(x = 0,7\)

d) \(D = \frac{1}{{x\left( {x + 1} \right)}} + \frac{1}{{\left( {x + 1} \right)\left( {x + 2} \right)}} + \frac{1}{{x + 2}}\) tại \(\frac{1}{{23}}\)

Rút gọn phân thức \(\frac{{a\left( {7 - b} \right)}}{{b\left( {{b^2} - 49} \right)}}\), ta nhận được

A. \(\frac{a}{{b\left( {b - 7} \right)}}\)

B. \(\frac{a}{{b\left( {b + 7} \right)}}\)

C. \( - \frac{a}{{b\left( {b + 7} \right)}}\)

D. \(\frac{a}{{b\left( {7 - b} \right)}}\)

Tử và mẫu của phân thức \(\frac{{\left( {x - 1} \right)\left( {x + 1} \right)}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\)có nhân tử chung là x−1. Viết phân thức nhận được sau khi chia cả tử và mẫu của phân thức này cho nhân tử chung đó. So sánh phân thức mới nhận được với phân thức đã cho. 

Phân tích tử và mẫu của phân thức \(\frac{{2{{\rm{x}}^2} + 2{\rm{x}}}}{{{x^2} - 1}}\) thành nhân tử và tìm các nhân tử chung của chúng 

Chia cả tử và mẫu của phân thức \(\frac{{2{{\rm{x}}^2} + 2{\rm{x}}}}{{{x^2} - 1}}\) cho các nhân tử chung, ta nhận được một phân thức mới bằng phân thức đã cho nhưng đơn giản hơn

Thực hiện rút gọn một phân thức như hình bên . Hỏi bạn tròn làm đúng hay sai/ Vì sao?

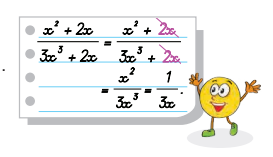
Tìm a sao cho hai phân thức sau bằng nhau: \(\frac{{{\rm{ - a}}{{\rm{x}}^2}{\rm{ -  ax}}}}{{{x^2} - 1}}\) và \(\frac{{3{\rm{x}}}}{{x - 1}}\)

Cho hai phân thức: \(\frac{1}{{2{{\rm{x}}^2} + 2{\rm{x}}}}\)và \(\frac{1}{{3{{\rm{x}}^2} - 6{\rm{x}}}}\). Phân tích các mẫu thức của hai phân thức đã cho thành nhân tử

Rút gọn các phân thức sau:

\(a)\frac{{5{\rm{x}} + 10}}{{25{{\rm{x}}^2} + 50}}\)

\(b)\frac{{45{\rm{x}}\left( {3 - x} \right)}}{{15{\rm{x}}{{\left( {x - 3} \right)}^3}}}\)

\(c)\frac{{{{\left( {{x^2} - 1} \right)}^2}}}{{\left( {x + 1} \right)\left( {{x^3} + 1} \right)}}\)

Cho phân thức \(P = \frac{{x + 1}}{{{x^2} - 1}}\)

a) Rút gọn phân thức đã cho, kí hiệu Q là phân thức nhận được

b) Tính giá trị của P và Q tại x = 11. So sánh haii kết quả đó.

Cho phân thức \(P = \frac{{2{{\rm{x}}^3} + 6{{\rm{x}}^2}}}{{2{{\rm{x}}^3} - 18{\rm{x}}}}\)

a) Viết điều kiện xác định và rút gọn phân thức P

b) Có thể tính giá trị của P tại x = −3 được không? Vì sao

c) Tính giá trị của phân thức P tại x = 4

d) Với giá trị nguyên nào của x thì P nhận giá trị nguyên?

Cho biểu thức:

\(P = \left( {\frac{{x + y}}{{1 - xy}} + \frac{{x - y}}{{1 + xy}}} \right):\left(1 + \frac{{{x^2} + {y^2} + 2{{\rm{x}}^2}{y^2}}}{{1 - {x^2}{y^2}}}\right)\)

Trong đó x và y là hai biến thỏa mãn điều kiện \({x^2}{y^2} - 1 \ne 0\)

a) Tính tổng \(A = \frac{{x + y}}{{1 - xy}} + \frac{{x - y}}{{1 + xy}}\) và \(B = 1 + \frac{{{x^2} + {y^2} + 2{{\rm{x}}^2}{y^2}}}{{1 - {x^2}{y^2}}}\)

b) Từ kết quả câu a) hãy thu gọn P và giải thích tại sao giá trị của P không phụ thuộc vào giá trị của biến y.

c) Chứng minh đẳng thức: \(P = 1 - \frac{{{{\left( {1 - x} \right)}^2}}}{{1 - {x^2}}}\)

d) Sử dụng câu c) hãy tìm các giá trị của x và y sao cho P = 1

Cho biểu thức \(P = \frac{{{x^2} - 6x + 9}}{{9 - {x^2}}} + \frac{{4x + 8}}{{x + 3}}\).

Rút gọn biểu thức \(P\).