Cho \(\widehat {AOC} = {60^0}\). Vẽ tia \(OB\) sao cho \(OA\) là tia phân giác của \(\widehat {BOC}\). Tính số đo của \(\widehat {AOB}\) và \(\widehat {BOC}\).
-
A.
\(\widehat {AOB} = 70^\circ ;\,\widehat {BOC} = 140^\circ \)
-
B.
\(\widehat {AOB} = 90^\circ ;\,\widehat {BOC} = 120^\circ \)
-
C.
\(\widehat {AOB} = 120^\circ ;\,\widehat {BOC} = 60^\circ \)
-
D.
\(\widehat {AOB} = 60^\circ ;\,\widehat {BOC} = 120^\circ \)
Sử dụng: Nếu tia \(Ot\) là tia phân giác của \(\widehat {xOy}\) thì \(\widehat {xOt} = \widehat {yOt} = \dfrac{{\widehat {xOy}}}{2}\)
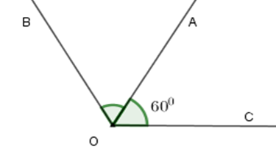
Vì tia \(OA\) là tia phân giác của \(\widehat {BOC}\) nên ta có
\(\widehat {AOB} = \widehat {AOC} = \dfrac{{\widehat {BOC}}}{2}\) nên \(\widehat {AOB} = 60^\circ ;\,\widehat {BOC} = 2.\widehat {AOC} = 2.60^\circ = 120^\circ \)
Vậy \(\widehat {AOB} = 60^\circ ;\,\widehat {BOC} = 120^\circ \).
Đáp án : D







