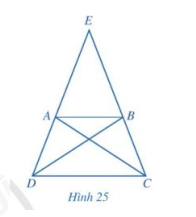
Cho hình thang cân ABCD có AB // CD , AB < CD, E là giao điểm của AD và BC (Hình 25)
a) So sánh các cặp góc: \(\widehat {E{\rm{D}}C}\) và \(\widehat {EC{\rm{D}}}\); \(\widehat {E{\rm{A}}B}\) và \(\widehat {EBA}\).
b) So sánh các cặp đoạn thẳng: EA và EB, ED và EC. Từ đó, hãy so sánh AD và BC.
c) Hai tam giác ADC và BCD có bằng nhau hay không? Từ đó, hãy so sánh AC và BD
Quan sát hình 25.
a, Do ABCD là hình thang cân nên.
\(\widehat {ADC} = \widehat {BCD}\)hay \(\widehat {EDC} = \widehat {ECD}\)
Do ABCD là hình thang cân nên
\(\widehat {BAD} = \widehat {ABC}\left( 1 \right)\)
Mà:
\(\begin{array}{l}\widehat {BAD} + \widehat {EAB} = {180^0}\\\widehat {ABC} + \widehat {EBA} = {180^0}\end{array}\)
Suy ra:
\(\begin{array}{l}\widehat {BAD} + \widehat {EAB} = \widehat {ABC} + \widehat {EBC}\\ \Rightarrow \widehat {EAB} = \widehat {EBA}\end{array}\)(do(1))
b, Do \(\widehat {EAB} = \widehat {EBA}\) suy ra \(\Delta EAB\)cân tại E nên EA = EB
Do \(\widehat {EDC} = \widehat {ECD}\) suy ra \(\Delta ECD\)cân tại E nên ED = EC
Mà: ED = EC
Suy ra EA + AD = EB + BC
Suy ra AD = BC (do EA = EB)
c, Xét \(\Delta ADC\) và \(\Delta BCD\) có:
AD = BC
\(\widehat {ADC} = \widehat {BCD}\)
DC chung
Suy ra: \(\Delta ADC = \Delta BCD(c.g.c) \Rightarrow AC = BD\)

Các bài tập cùng chuyên đề
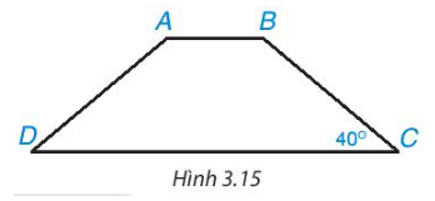
Tính các góc của hình thang cân ABCD (AB // CD), biết \(\widehat C = {40^o}\)(H.3.15).
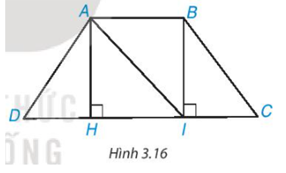
Cho hình thang cân ABCD, AC // CD và AB < CD (H.3.16).
a) Từ A và B kẻ AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD. Chứng minh rằng AH = BI bằng cách chứng minh ∆AHI = ∆IBA.
b) Chứng minh ∆AHD = ∆BIC, từ đó suy ra AD = BC
Cho tứ giác ABCD như Hình 3.18. Biết rằng \(\widehat A = \widehat B = \widehat {{D_1}}\). Chứng minh rằng AD = BC.
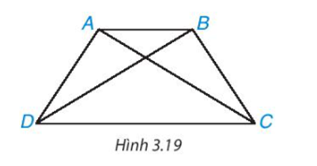
Cho hình thang cân ABCD, kẻ hai đường chéo AC, BD (H.3.19). Hãy chứng minh ∆ACD = ∆BDC. Từ đó suy ra AC = BD
Cho tam giác ABC cân tại A. Kẻ một đường thẳng d song song với BC, d cắt cạnh AB tại D và cắt cạnh AC tại E (H.3.20).
a) Tứ giác DECB là hình gì?
b) Chứng minh BE = CD.
Hình thang trong Hình 3.23 có là hình thang cân không? Vì sao
Vẽ hình thang cân ABCD (AB // CD) biết đáy lớn CD dài 4 cm, cạnh bên dài 2 cm và đường chéo dài 3 cm.
Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB // CD) cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng EC = ED.
a) Cho hình thang cân \(ABCD\) có hai đáy là \(AB\) và \(CD\) (\(AB > CD\). Qua \(C\) vẽ đường thẳng song song với \(AD\) và cắt \(AB\) tại \(E\) (Hình 6a)
i) Tam giác \(CEB\) là tam giác gì? Vì sao?
ii) So sánh \(AD\) và \(BC\)
b) Cho hình thang cân \(MNPQ\) có hai đáy là \(MN\) và \(PQ\) (Hình 6). So sánh \(MP\) và \(NQ\)
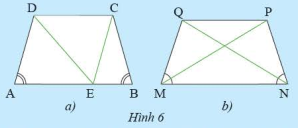
Tìm các đoạn thẳng bằng nhau trong hình thang cân \(MNPQ\) có hai đáy \(MN\) và \(PQ\)
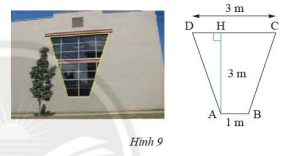
Một khung cửa sổ hình thang cân có chiều cao 3m, hai đáy là 3m và 1m (Hình 9). Tìm độ dài hai cạnh bên và hai đường chéo.
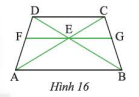
Cho hình thang cân \(ABCD\) có \(AB\) // \(CD\). Qua gia điểm \(E\) của \(AC\) và \(BD\), ta vẽ đường thẳng song song với \(AB\) và cắt \(AD\), \(BC\) lần lượt tại \(F\) và \(G\) (Hình 16). Chứng minh rằng \(EG\) là tia phân giác của góc \(CEB\).
Cho hình thang cân \(ABCD\) (\(AB\) // \(CD\)) có \(\widehat {\rm{A}} = 65^\circ \). Số đo góc \(C\) là:
A. \(115^\circ \)
B. \(95^\circ \)
C. \(65^\circ \)
D. \(125^\circ \)
Hình thang cân có những tính chất gì? Có những dấu hiệu nào để nhận biết một tứ giác là hình thang cân?
Cho hình thang cân, ABCD có AB //CD. Chứng minh \(\widehat {A{\rm{DB}}} = \widehat {BCA}\)
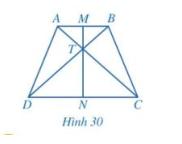
Cho hình thang cân ABCD có AB // CD, AB < CD. Gọi M, N lần lượt là trung điểm của cạnh AB, CD và T là giao điểm của AC và BD (hình 30)
a) \(\widehat {TA{\rm{D}}} = \widehat {TBC},\widehat {T{\rm{D}}A} = \widehat {TCB}\)
b) \(TA = TB,T{\rm{D}} = TC\)
c) MN là đường trung trực của cả hai đoạn thẳng AB và CD
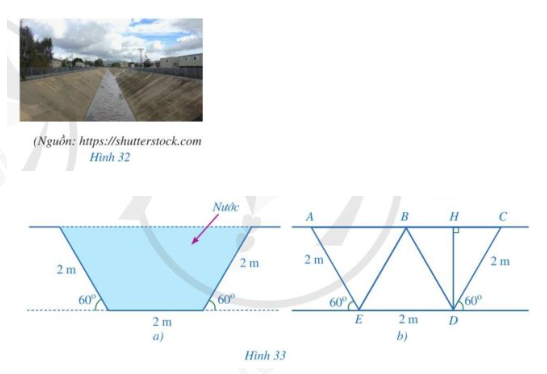
Hình 33a là mặt cắt đứng phần chứa nước của một con mương (hình 32) khi đầy nước có dạng hình thang cân. Người ta mô tả lại bằng hình học mặt cắt đứng của con mương đó ở Hình 33b với BD // AE (B thuộc AC. H là hình chiếu của D trên đường thẳng BC.
a) Chứng minh rằng các tam giác BCD, BDE, ABE là các tam giác đều
b) Tính độ dài của DH, AC
c) Tính diện tích mặt cắt đứng phần chứa nước của con mương đó khi đầy nước.
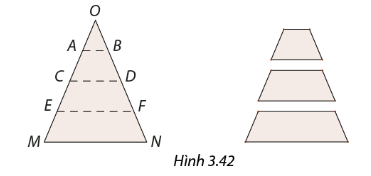
Trong Hình 3.42, giải thích vì sao \(\Delta OAB\) và \(\Delta OCD\) là các tam giác cân tại O. Em hãy so sánh các cặp cạnh \(OA\) và \(OB,OC\) và \(OD\). Từ đó có thể kết luận gì về hai đoạn thẳng \(AC\) và \(BD\)?
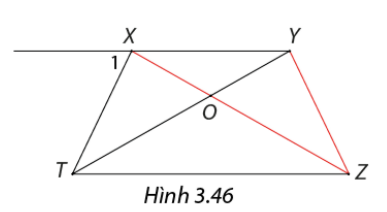
Trong Hình 3.46, cho \(\widehat {{X_1}} = \widehat {XTZ} = \widehat {YZT},XT = 6,OT = 7\) và \(OY = 4\). Tứ giác \(XYZT\) là hình gì? Tìm độ dài \(XZ\) và \(YZ\).
Mai cho rằng hình thang có hai cạnh bên bằng nhau là hình thang cân. Bạn Mai nói có đúng không? Vì sao?
Cho \(ABC\) là tam giác cân tại A. Lấy điểm M trên cạnh \(AB\), điểm N trên cạnh \(AC\) sao cho \(AM = AN\). Chứng minh rằng \(BMNC\) là hình thang cân.
Tính các góc của hình thang ABCD (AB,CD là hai đáy) biết \(\widehat A = 2\widehat D\), \(\widehat B = \widehat C + 40^\circ \).
Cho hình thang cân ABCD với hai đường thẳng chứa hai cạnh bên AD, BC cắt nhau tại S. Gọi O là giao điểm của hai đường chéo AC và BD. Chứng minh đường thẳng SO đi qua trung điểm của AB, đi qua trung điểm của CD.
Cho hình thang cân ABCD với hai đáy AB và CD, đường chéo AC vuông góc với cạnh bên AD, tia CA là tia phân giác của góc C. Tính chu vi của hình thang đó biết rằng \(AD = 2cm\).
Điền cụm từ thích hợp vào chỗ trống.
a) Hình thang cân là ............................................................................................ bằng nhau.
b) Hình thang có ....................................................................................... là hình thang cân.
c) Hai cạnh bên của hình thang cân .....................................................................................
d) Hình thang cân ABCD (AB // CD) có AD = ...................; AC = ..................; \(\widehat A = \).................. ; \(\widehat C = \)..................
Hình thang cân ABCD (AB // CD, AB < CD) có các đường thẳng AD, BC cắt nhau tại I, các đường thẳng AC, BD cắt nhau tại J. Chứng minh rằng đường thẳng IJ là đường trung trực của đoạn thẳng AB.
Cho hình thang cân ABCD có đáy nhỏ BC. Hạ BH ⊥ AD, CE ⊥ AD.
a) Chứng minh AH = ED.
b) Cho BH = 4 cm, và \(\widehat A = 45^\circ .\) Tính độ dài ED.
Cho hình thang cân ABCD (AB // CD) có AB = AD. Biết \(\widehat {ABD} = 30^\circ \), tính số đo góc của hình thang đó.
Tính số đo các góc của tứ giác ABCD trong Hình 3.16.

Cho hình thang cân ABCD có AB//CD, DB là tia phân giác của góc D, \(DB \bot BC\). Biết \(AB = 4cm\). Tính chu vi của hình thang đó.










Danh sách bình luận