Cho \({S_1}\), \({S_2}\) là diện tích các hình phẳng được mô tả trong hình 3. Tính \(\frac{{{S_1}}}{{{S_2}}}\).
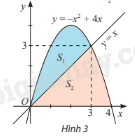
Diện tích \({S_1} + {S_2}\) chính là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = - {x^2} + 4x\), trục hoành và các đường thẳng \(x = 0\), \(x = 4\). Do đó \({S_1} + {S_2} = \int\limits_0^4 {\left( { - {x^2} + 4x} \right)dx} \)
Hình phẳng \({S_1}\) được giới hạn bởi các đồ thị hàm số \(y = - {x^2} + 4x\), \(y = x\) và các đường thẳng \(x = 0\), \(x = 3\). Do đó \({S_1} = \int\limits_0^3 {\left[ {\left( { - {x^2} + 4x} \right) - x} \right]dx} \).
Từ đó tính được \({S_2}\) và tỉ số \(\frac{{{S_1}}}{{{S_2}}}\).
Diện tích \({S_1} + {S_2}\) chính là diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = - {x^2} + 4x\), trục hoành và các đường thẳng \(x = 0\), \(x = 4\). Do đó
\({S_1} + {S_2} = \int\limits_0^4 {\left( { - {x^2} + 4x} \right)dx} = \left. {\left( {\frac{{ - {x^3}}}{3} + 2{x^2}} \right)} \right|_0^4 = \frac{{32}}{3}\).
Hình phẳng \({S_1}\) được giới hạn bởi các đồ thị hàm số \(y = - {x^2} + 4x\), \(y = x\) và các đường thẳng \(x = 0\), \(x = 3\). Do đó
\({S_1} = \int\limits_0^3 {\left[ {\left( { - {x^2} + 4x} \right) - x} \right]dx} = \int\limits_0^3 {\left( { - {x^2} + 3x} \right)dx} = \left. {\left( { - \frac{{{x^3}}}{3} + \frac{{3{x^2}}}{2}} \right)} \right|_0^3 = \frac{9}{2}\).
Suy ra \({S_2} = \frac{{32}}{3} - \frac{9}{2} = \frac{{37}}{6}\) và \(\frac{{{S_1}}}{{{S_2}}} = \frac{9}{2}:\frac{{37}}{6} = \frac{{27}}{{37}}\)

Các bài tập cùng chuyên đề
Tốc độ chuyển động \(v{\rm{ }}\left( {{\rm{m/s}}} \right)\) của một ca nô trong khoảng thời gian 40 giây được thể hiện như hình 1. Quãng đường đi được của ca nô trong khoảng thời gian này là:
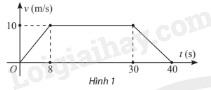
A. 400 m
B. 350 m
C. 310 m
D. 200 m
Cho hàm số \(y = f\left( x \right)\). Đồ thị của hàm số \(y = f'\left( x \right)\) là đường cong trong hình 2. Biết rằng diện tích các phần hình phẳng \(A\) và \(B\) lần lượt là \({S_A} = 2\) và \({S_B} = 3\). Nếu \(f\left( 0 \right) = 4\) thì giá trị của \(f\left( 5 \right)\) bằng
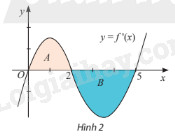
A. \(3\)
B. \(5\)
C. \(9\)
D. \( - 1\)
Một chất điểm đang chuyển động với tốc độ \({v_0} = 1{\rm{ }}\left( {{\rm{m/s}}} \right)\) thì tăng tốc với gia tốc không đổi \(a = 3{\rm{ m/}}{{\rm{s}}^2}\). Hỏi tốc độ của chất điểm là bao nhiêu sau 10 giây kể từ khi bắt đầu tăng tốc?
Tốc độ tăng dân số của một thành phố trong một số năm được ước lượng bởi công thức \(P'\left( t \right) = 20.{\left( {1,106} \right)^t}\) với \(0 \le t \le 7\), trong đó \(t\) là thời gian tính theo năm và \(t = 0\) ứng với đầu năm 2015, \(P\left( t \right)\) là dân số của thành phố tính theo nghìn người. Cho biết dân số của thành phố đầu năm 2015 là 1008 nghìn người.
a) Tính dân số của thành phố ở thời điểm đầu năm 2020 (làm tròn đến nghìn người).
b) Tính tốc độ tăng dân số trung bình hằng năm của thành phố trong giai đoạn từ đầu năm 2015 đến đầu năm 2020.
Sau khi được thả rơi tự do từ độ cao 100 m, một vật rơi xuống với tốc độ \(v\left( t \right) = 10t{\rm{ }}\left( {{\rm{m/s}}} \right)\), trong đó \(t\) là thời gian tính theo giây kể từ khi thả vật.
a) Tính quãng đường \(s\left( t \right)\) vật di chuyển được sau thời gian \(t\) giây (trong khoảng thời gian vật đang rơi)
b) Sau bao nhiêu giây thì vật chạm đất? Tính tốc độ rơi trung bình của vật.
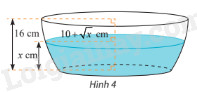
Nếu cắt chậu nước có hình dạng như hình 4 bằng mặt phẳng song song và cách mặt đáy \(x\) (cm) \(\left( {0 \le x \le 16} \right)\) thì mặt cắt là hình tròn có bán kính \(\left( {10 + \sqrt x } \right)\) (cm). Tính dung tích của chậu.
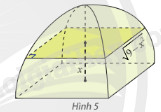
Một chiếc lều mái vòm có hình dạng như hình 5. Nếu cắt lều bằng mặt phẳng song song với mặt đáy và cách mặt đáy một khoảng \(x{\rm{ }}\left( {\rm{m}} \right)\) \(\left( {0 \le x \le 3} \right)\) thì được hình vuông có cạnh \(\sqrt {9 - {x^2}} {\rm{ }}\left( {\rm{m}} \right)\). Tính thể tích của lều.
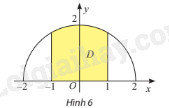
Trên mặt phẳng toạ độ \(Oxy\), vẽ nửa đường tròn tâm \(O\), bán kính \(r = 2\) nằm phía trên trục \(Ox\). Gọi \(D\) là hình phẳng giới hạn bởi nửa đường tròn, trục \(Ox\) và hai đường thẳng \(x = - 1\), \(x = 1\). Tính thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\).
Gọi \(H\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = {2^x}\), trục hoành và hai đường thẳng \(x = 1,x = 2\).
a) Tính diện tích \(S\) của hình phẳng \(H\).
b) Tính thể tích \(V\) của khối tròn xoay tạo thành khi cho hình phẳng \(H\) quay quanh trục \(Ox\).
Gọi \(H\) là hình phẳng giới hạn bởi đồ thị \(y = {x^2} - 2x\), trục hoành và hai đường thẳng \(x = 0,x = 2\).
a) Tính diện tích \(S\) của hình phẳng \(H\).
b) Tính thể tích \(V\) của khối tròn xoay tạo thành khi cho hình phẳng \(H\) quay quanh trục \(Ox\).
Xét hình phẳng giới hạn bởi các đường \(y = \sqrt x ,y = \frac{{{x^2}}}{8},x = 0,x = 4\).
a) Tính diện tích hình phẳng;
b) Tính thể tích khối tròn xoay sinh ra khi quay hình phẳng xung quanh trục Ox.
Cho \(D\) là hình phẳng giới hạn bởi đồ thị của hàm số \(y = 2{x^3}\), trục hoành và hai đường thẳng \(x = - 1,x = 1\).
a) Tính diện tích của \(D\).
b) Tính thể tích của khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\).
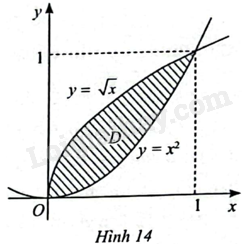
Gọi \(D\) là hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = {x^2}\) và \(y = \sqrt x \) (Hình 14).
a) Tính diện tích của \(D\).
b) Tinh thể tích của khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\).
Một cột bê tông hình trụ có chiều cao 9 m. Nếu cắt cột bê tông bằng mặt phẳng nằm ngang cách chân cột \(x\left( m \right)\) thì mặt cắt là hình tròn có bán kính \(1 - \frac{{\sqrt x }}{4}\left( m \right)\) với \(0 \le x \le 9\). Tính thể tích của cột bê tông (kết quả làm tròn đến hàng phần trăm của mét khối).
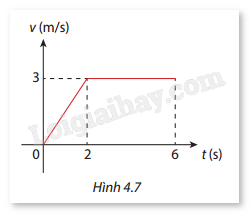
Hình 4.7 là đồ thị vận tốc \(v(t)\) của một vật (t = 0 là thời điểm vật bắt đầu chuyển động).
a) Viết công thức của hàm số \(v(t)\) với \(t \in [0;6]\).
b) Tính quãng đường vật di chuyển được trong 6 giây đầu tiên.
Một quả bóng được ném lên từ độ cao \(1,5m\) với vận tốc ban đầu \(24m/s\). Biết gia tốc của quả bóng là \(a = - 9,8m/{s^2}\).
a) Tính vận tốc của quả bóng tại thời điểm 1 giây sau khi được ném lên.
b) Tính quãng đường quả bóng đi được từ lúc ném lên đến khi chạm đất lần đầu.
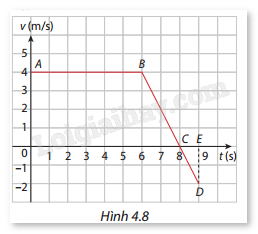
Đường gấp khúc ABD trong Hình 4.8 là đồ thị vận tốc \(v(t)\) của một vật (t = 0 là thời điểm vật bắt đầu chuyển động). Trong khoảng thời gian mà \(v < 0\)thì vật chuyển động ngược chiều với khoảng thời gian mà \(v > 0\).
a) Viết công thức của hàm số \(v(t)\) với \(t \in [0;9]\).
b) Biết rằng quãng đường vật đi chuyển với vận tốc \(v = v(t)\) từ thời điểm \(t = a\) đến thời điểm \(t = b\) là \(s = \int_a^b | v(t)|{\mkern 1mu} dt\), tính quãng đường vật di chuyển được trong 9 giây kể từ khi vật bắt đầu chuyển động.
c) Tính tổng diện tích của hình thang \(OABC\) và tam giác \(CDE\) rồi so sánh với kết quả ở câu b.
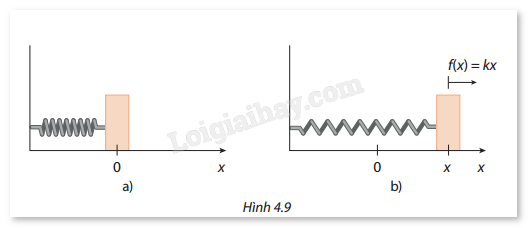
Một lò xo có chiều dài tự nhiên là \({l_0} = 10{\mkern 1mu} {\rm{cm}}\)(Hình 4.9a). Để kéo giãn lò xo \(x{\mkern 1mu} ({\rm{m}})\) cần một lực có độ lớn \(f(x) = kx{\mkern 1mu} ({\rm{N}})\), trong đó \(k\) là độ cứng của lò xo và có giá trị không đổi. (Hình 4.9b).
a) Tìm \(k\), biết dưới tác dụng của một lực 40 N, lò xo bị giãn và chiều dài của lò xo khi ấy là \({l_1} = 15{\mkern 1mu} {\rm{cm}}\).
b) Nếu một lực có độ lớn \(f(x){\mkern 1mu} ({\rm{N}})\) làm biến dạng lò xo từ độ giãn \(a{\mkern 1mu} ({\rm{m}})\) đến \(b{\mkern 1mu} ({\rm{m}})\) thì công của lực đó được cho bởi công thức \(A = \int_a^b f (x){\mkern 1mu} dx\)(J). Tính công của một lực làm lò xo biến dạng từ chiều dài 15 cm đến 18 cm.
Hiệu suất của tim là lưu lượng máu được bơm bởi tim trên một đơn vị thời gian (lưu lượng máu chảy vào động mạch chủ). Để đo hiệu suất của tim, người ta bơm \(A\) (mg) chất chỉ thị màu vào tâm nhĩ phải, chảy qua tim rồi vào động mạch chủ và đo nồng độ chất chỉ thị màu còn lại ở tim đến thời điểm \(T(s)\) khi chất chỉ thị màu tan sạch. Gọi \(c(t)\) là nồng độ \(({\rm{mg/l}})\) chất chỉ thị màu tại thời điểm \(t\) (s) thì hiệu suất của tim được xác định bởi:
\(F = \frac{A}{{\int_0^T c (t)dt}}{\mkern 1mu} ({\rm{l/s}})\)
Tính hiệu suất của tim khi bơm 8 mg chất chỉ thị màu vào tâm nhĩ phải, biết rằng \(c(t) = \frac{1}{4}t(12 - t)\) với \(0 \le t \le 12\).
Ở \({45^\circ }C\), phản ứng hóa học phân hủy \({N_2}{O_5}\) xảy ra theo phương trình:
\({N_2}{O_5} \to 2N{O_2} + \frac{1}{2}{O_2}\)
với nồng độ \(c(t)\) (mol/L) của \({N_2}{O_5}\) \((c(t) > 0)\) tại thời điểm \(t\) giây (t \( \ge 0\)) thỏa mãn \(c'(t) = - 0,0005c(t)\). Biết khi \(t = 0\), nồng độ ban đầu của \({N_2}{O_5}\) là 0,05 mol/L.
a) Xét hàm số \(y(t) = \ln c(t)\) với \(t \ge 0\). Tính \(y'(t)\), từ đó tìm \(y(t)\).
b) Biết rằng nồng độ trung bình của \({N_2}{O_5}\) (mol/L) từ thời điểm \(a\) giây đến thời điểm \(b\) giây (\(a < b\)) được cho bởi công thức:
\(\frac{1}{{b - a}}\int_a^b c (t){\mkern 1mu} dt\)
Tính nồng độ trung bình của \({N_2}{O_5}\) từ thời điểm 10 giây đến thời điểm 20 giây.
Trọng lực của Trái Đất tác dụng lên một vệ tinh trong quá trình vệ tinh này được phóng lên từ mặt đất tới vị trí cách tâm Trái Đất \(r\) (m) xác định bởi công thức: \(F(r) = \frac{{GMm}}{{{r^2}}}\), trong đó: \(M = {6.10^{24}}{\mkern 1mu} {\rm{kg}}\) là khối lượng Trái Đất, \(m\) (kg) là khối lượng vệ tinh và \(G = 6.67 \times {10^{ - 11}}{\mkern 1mu} {\rm{N}}{{\rm{m}}^2}/{\rm{k}}{{\rm{g}}^2}\) là hằng số hấp dẫn. Trọng lực này sinh công \(W = \int_a^b F (h){\mkern 1mu} dh\) (J) khi vệ tinh thay đổi từ cách tâm Trái Đất \(a\) (m) lên vị trí cách tâm Trái Đất \(b\)(m). Tính công tối thiểu để phóng một vệ tinh nặng \(m = 1\,\,000{\mkern 1mu} {\rm{kg}}\) từ mặt đất lên độ cao \(35\,\,780{\mkern 1mu} {\rm{km}}\) so với mặt đất, biết bán kính Trái Đất là \(6\,\,370{\mkern 1mu} {\rm{km}}\).
Một ô tô đang chạy với vận tốc \(20{\mkern 1mu} {\rm{m/s}}\) thì người lái đạp phanh, từ thời điểm đó ô tô chuyển động với vận tốc \(v(t) = - 5t + 20{\mkern 1mu} {\rm{(m/s)}}\), trong đó \(t\) là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển thêm một quãng đường dài bao nhiêu mét?
Một bồn chứa nước bắt đầu bị rỉ từ đáy. Tốc độ nước chảy ra từ đáy bồn tại thời điểm \(t\) phút được cho bởi hàm số \(V'(t) = 200 - 4t\)(lít/phút) với \(0 \le t \le 50\) và \(V(t)\) là hàm số cho biết thể tích nước trong bồn tại thời điểm \(t\). Tính lượng nước chảy ra khỏi bồn trong 10 phút đầu tiên từ khi bồn bị rỉ nước.
Trong kinh tế, nếu hàm số \(C(x)\) là tổng chi phí khi sản xuất \(x\) đơn vị hàng hóa nào đó thì tốc độ thay đổi tức thời của chi phí theo số lượng sản phẩm được sản xuất \(C'(x)\) được gọi là chi phí biên. Chi phí biên \(C'(n)\) là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ \(n\) sản phẩm lên \(n + 1\) sản phẩm. Giả sử chi phí biên khi sản xuất \(x\) sản phẩm của một công ty là \(C'(x) = 2x + 80\) (USD/ sản phẩm) thì tổng chi phí sản xuất tăng lên bao nhiêu nếu sản phẩm sản xuất ra tăng từ 40 sản phẩm lên 50 sản phẩm?
Tốc độ tăng cân nặng của một bé gái trong độ tuổi từ 0 đến 36 tháng được ước tính bởi hàm số \(f'(t) = 0,00093{t^2} - 0,04792t + 0,76806{\mkern 1mu} \) (kg/tháng) với \(f(t)\) là cân nặng của bé gái lúc \(t\) tháng tuổi. Hãy ước tính cân nặng của một bé gái 5 tháng tuổi, biết cân nặng trung bình của bé gái khi mới sinh là \(3,3{\mkern 1mu} {\rm{kg}}\).
Một vật chuyển động trong 3 giờ với vận tốc \(v\) (km/h) phụ thuộc vào thời gian \(t\) (h) có đồ thị là một phần của đường parabol có đỉnh \(I(2;9)\) và trục đối xứng song song với trục tung như Hình 4.30. Tính quãng đường mà vật di chuyển được trong 3 giờ đó.
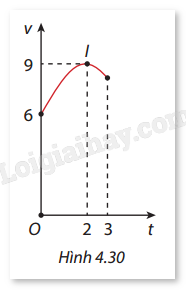
A. \(25,25{\mkern 1mu} {\rm{km}}\)
B. \(24,25{\mkern 1mu} {\rm{km}}\)
C. \(24,75{\mkern 1mu} {\rm{km}}\)
D. \(26,75{\mkern 1mu} {\rm{km}}\)
Một cái cổng hình parabol như Hình 4.31. Chiều cao \(GH = 4{\mkern 1mu} {\rm{m}}\), chiều rộng \(AB = 4{\mkern 1mu} {\rm{m}},AC = BD = 0,9{\mkern 1mu} {\rm{m}}\). Người ta làm hai cánh cổng khi đóng lại là hình chữ nhật \(CDEF\) tô đậm với giá 1.200.000 đồng/m², phần còn lại làm khung hoa sắt với giá 900.000 đồng/m².
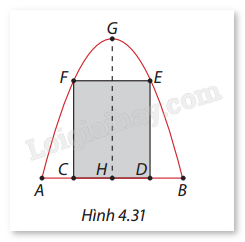
A. 11 445 000 đồng.
B. 4 077 000 đồng.
C. 7 368 000 đồng.
D. 11 370 000 đồng.
Một con lắc lò xo dao động điều hòa theo phương ngang trên mặt phẳng không ma sát có vận tốc tại thời điểm \(t\) giây là \(v = 4\cos (t)\) (cm/s). Tìm li độ của con lắc tại thời điểm \(t = \frac{{2\pi }}{3}\) giây, biết khi \(t = \frac{\pi }{2}\) giây thì con lắc có li độ \(x = 4\) cm.
A. \(\sqrt 3 \)cm.
B. 2 cm.
C. \(2\sqrt 3 \) cm.
D. 4 cm.
Tích phân \(\pi \int\limits_1^3 {{{\left( {x - 1} \right)}^2}dx} \) dùng để tính một trong các đại lượng sau, đó là các đại lượng nào?
A. Diện tích hình phẳng giới hạn bởi các đường: \(y = {\left( {x - 1} \right)^2},{\rm{ }}y = 0,{\rm{ }}x = 1,{\rm{ }}x = 3\).
B. Thể tích khối tròn xoay hình thành khi quay hình phẳng giới hạn bởi các đường: \(y = x - 1,{\rm{ }}y = 0,{\rm{ }}x = 1,{\rm{ }}x = 3\) quay quanh trục Ox.
C. Diện tích hình phẳng giới hạn bởi các đường: \(y = {\left( {x - 1} \right)^2},{\rm{ }}y = 0,{\rm{ }}x = 2,{\rm{ }}x = 3\).
D. Thể tích khối tròn xoay hình thành khi quay hình phẳng giới hạn bởi các đường: \(y = x - 1,{\rm{ }}y = 0,{\rm{ }}x = 2,{\rm{ }}x = 3\) quay quanh trục Ox.
Một ô tô đang chạy với vận tốc 15 m/s thì tăng tốc, chuyển động thành chuyển động nhanh dần đều với gia tốc \(a = 3t - 8\left( {m/{s^2}} \right)\), trong đó t là khoảng thời gian tính bằng giây kể từ lúc tăng vận tốc.
a) Biết vận tốc của ô tô là \(v\left( t \right) = \frac{a}{2}{t^2} + bt + c\) với \(a,b,c\) là các số nguyên. Tính \(a + b + c\).
b) Quãng đường ô tô đi được sau 10 giây kể từ lúc bắt đầu tăng tốc là bao nhiêu mét? (làm tròn đến hàng đơn vị).







Danh sách bình luận