Cho hình thang \(ABCD\) có hai đáy là \(AB\), \(CD\) và có hai đường chéo bằng nhau (Hình 10). Vẽ đường thẳng đi qua \(C\), song song với \(BD\) và cắt \(AB\) tại \(E\).
a) Tam giác \(CAE\) là tam giác gì? Vì sao?
b) So sánh tam giác \(ABD\) và tam giác \(BAC\)
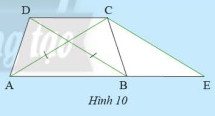
Sử dụng tính chất của hình thang cân chứng minh \(\Delta CAE\) cân; \(\Delta ABD = \Delta BAC\)
a) Vì \(ABCD\) là hình thang cân (gt) nên \(AC = BD\) và \(AB\;{\rm{//}}\;CD\)
Xét \(\Delta BCD\) và \(\Delta CBE\) ta có:
\(\widehat {DCB} = \widehat {CBE}\) (do \(AB\) // \(CD\))
\(BC\) chung
\(\widehat {CBD} = \widehat {BCE}\) (do \(CE\) // \(BD\))
Suy ra \(\Delta BCD = \Delta CBE\) (g-c-g)
Suy ra \(BD = CE\) (hai cạnh tương ứng)
Mà \(AC = BD\) (cmt)
Suy ra \(AC = EC\)
Vậy \(\Delta CAE\) cân tại \(C\)
b) Xét \(\Delta ABD\) và \(\Delta BAC\) ta có:
\(DA = BC\) (do \(ABCD\) là hình thang cân)
\(\widehat {DAB} = \widehat {CBA}\) (Do \(ABCD\) là hình thang cân)
\(AB\) chung
Suy ra \(\Delta ABD = \Delta BAC\) (c-g-c)

Các bài tập cùng chuyên đề
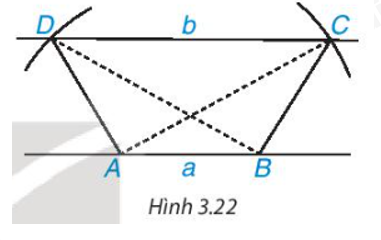
a) Vẽ hình thang có hai đường chéo bằng nhau theo các bước sau:
- Vẽ hai đường thẳng song song a, b. Trên a lấy hai điểm A, B.
- Vẽ hai cung tròn tâm A và B có cùng bán kính sao cho cung tròn tâm A cắt b tại C; cung tròn tâm B cắt b tại D và hai đoạn thẳng AC, BD cắt nhau. Hình thang ABCD có hai đường chéo AC và BD bằng nhau.
b) Hình thang ABCD có là hình thang cân không? Vì sao?
Cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy thì được hai hình thang. Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu (Hình 3.11). Hãy giải thích tại sao hình tạo thành cũng là một hình thang cân.
Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông góc với BD tại D, hai đường thẳng này cắt nhau tại E. Chứng minh rằng nếu EC = ED thì hình thang ABCD là hình thang cân.
Chứng minh rằng nếu tứ giác có hai đường chéo bằng nhau và một cặp cạnh đối bằng nhau thì tứ giác đó là một hình thang cân
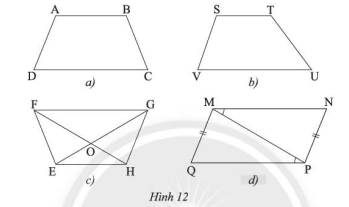
Sử dụng thước đo góc và thước đo độ dài để tìm hình thang cân trong các tứ giác ở Hình 12.
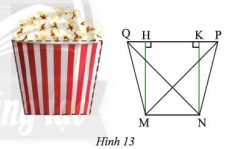
Mặt cắt của một li giấy đựng bỏng ngô có dạng hình thang cân \(MNPQ\) (Hình 13) với hai đáy \(MN = 6cm\), \(PQ = 10\)cm và độ dài hai đường chéo \(MN = NQ = 8\sqrt 2 \) cm. Tính độ dài đường chéo và cạnh bên của hình thang
Cho tứ giác \(ABCD\) có \(AB = AD\), \(BD\) là tia phân giác của góc \(B\). Chứng minh rằng \(ABCD\) là hình thang.
Cho tam giác nhọn \(ABC\) có \(AH\) là đường cao. Tia phân giác của góc \(B\) cắt \(AC\) tại \(M\). Từ \(M\) kẻ đường thẳng vuông góc với \(AH\) và cắt \(AB\) tại \(N\). Chứng minh rằng:
a) Tứ giác \(BCMN\) là hình thang
b) \(BN = MN\)
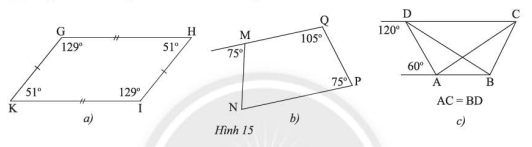
Tứ giác nào trong Hình 15 là hình thang cân?
Cho hình chữ nhật ABCD. Trên cạnh AB lấy hai điểm M, N sao cho \(AM = NB < \dfrac{1}{2}AB\). Chứng minh tứ giác MNCD là hình thang cân
Cho tam giác ABC cân tại A có hai đường phân giác BE và CK. Chứng minh tứ giác BKEC là hình thang cân.
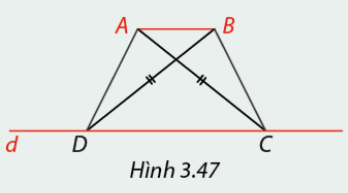
Cho đoạn thẳng \(AB\). Em hãy dựng điểm C và D trên \(d\) sao cho \(ABCD\) là hình thang có hai đường chéo \(AC = BD\) (Hình 3.47). Đo các góc \(\widehat C\) và \(\widehat D\) của hình thang \(ABCD\). Nêu nhận xét và từ đó hãy cho biết tứ giác \(ABCD\) là hình gì.
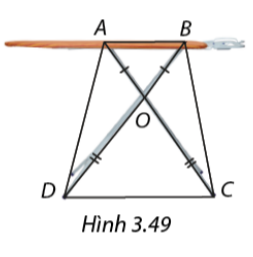
Để cầu là được thăng bằng khi là quần áo, người ta thiết kế hai chân \(AC,BD\) cắt nhau tại O sao cho \(OA = OB\) và \(OC = OD\) (Hình 3.49). Giải thích vì sao khi đó đường thẳng \(AB\) trên mặt cầu là song song với đường thẳng \(CD\) trên mặt đất. Tứ giác \(ABCD\) là hình gì?
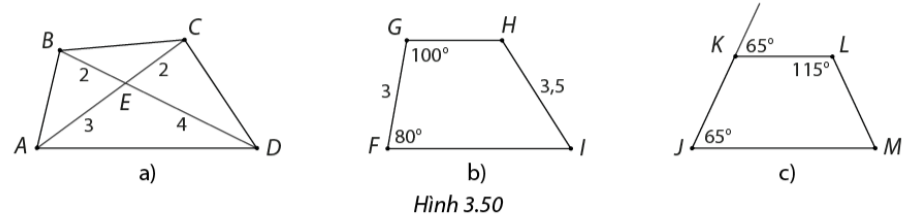
Tứ giác nào trong Hình 3.50 là hình thang hoặc hình thang cân?
Tứ giác \(ABCD\) có \(\widehat A = \widehat B\) và \(\widehat C = \widehat D\). Chứng minh rằng \(ABCD\) là hình thang cân.
Cho \(ABCD\) là hình bình hành có góc \(C\) là góc nhọn. Trên tia đối của tia \(DC\) lấy điểm \(E\) sao cho \(AD = AE\) ( \(E\) khác \(D\)). Chứng minh rằng \(ABCE\) là một hình thang cân.
Cho tam giác ABC vuông cân tại đỉnh A. Ghép thêm vào phía ngoài tam giác đó tam giác BCD vuông cân tại đỉnh B. Chứng minh tứ giác ABDC là một hình thang vuông (hình thang có một cạnh bên vuông góc với đáy).
Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông góc với BD tại D, hai đường thẳng này cắt nhau tại E. Chứng minh rằng nếu EC = ED thì hình thang ABCD là hình thang cân.
Tứ giác ABCD trong Hình 3.14 có phải là hình thang không? Vì sao?

Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BC, CA tại các điểm P, Q, R.
a) Chứng minh tứ giác APMR là hình thang cân.
b) Chứng minh rằng chu vi tam giác PQR bằng tổng độ dài MA + MB + MC.
c) Hỏi với vị trí nào của M thì tam giác PQR là tam giác đều.
Cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho AM = AN.
a) Tính số đo góc AMN theo góc A.
b) Tứ giác BMNC là hình gì? Vì sao?
c) Cho BM = MN = NC, chứng minh BN là phân giác của góc ABC, CM là phân giác của góc ACB.
Cho tứ giác ABCD có \(AB = BC\) và AC là tia phân giác của góc A. Chứng minh tứ giác ABCD là hình thang.
Tứ giác ABCD có \(\widehat A + \widehat D = \widehat B + \widehat C\). Chứng minh tứ giác ABCD là hình thang.
Cho tam giác ABC vuông cân tại A. Vẽ ra phía ngoài của tam giác ABC một tam giác BCD vuông cân tại B. Tứ giác ABDC là hình gì? Vì sao?
Hình thang ABCD (AB//CD) có \(\widehat {ACD} = \widehat {BDC}\). Chứng minh tứ giác ABCD là hình thang cân.
Cho tam giác ABC cân tại A. Trên tia đối của tia AB lấy điểm M, trên tia đối của tia AC lấy điểm N sao cho \(AM = AN.\) Chứng minh tứ giác MNBC là hình thang cân.
Cho tam giác ABC cân tại A, có hai đường cao BE và CD \(\left( {D \in AB,E \in AC} \right)\). Chứng minh tứ giác BDEC là hình thang cân.
Xét hai hình bình hành MNBA và MNCB.
a) Chứng minh A, B, C là ba điểm thẳng hàng;
b) Chứng minh B là trung điểm của AC;
c) Hỏi tam giác MAB thỏa mãn điều kiện gì để MNCA là một hình thang cân?
d) Lấy điểm D để tứ giác MNDC là hình bình hành. Hỏi tam giác MAB thỏa mãn điều kiện gì để MNDA là một hình thang cân?
Cho tam giác \(ABC\) cân tại \(A\). Lấy điểm \(M,N\) lần lượt trên cạnh \(AB,AC\) sao cho \(AM = AN\).
a) Chứng minh tứ giác \(BMNC\) là hình thang cân
b) Xác định vị trí các điểm \(M,N\) để \(BM = MN = NC\).
Cho tam giác đều \(ABC\) có độ dài cạnh là 6 cm. trên tia \(BA,CA\) lần lượt lấy điểm \(D,E\) sao cho \(AD = AE = 2cm\) (Hình 12)
a) Tứ giác \(BCDE\) là hình gì? Vì sao?
b) Tính độ dài đoạn thẳng \(CD\) (làm tròn kết quả đến hàng phần mười của centimet).