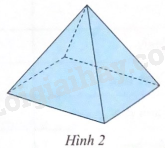
Nam làm một chiếc hộp hình chóp tứ giác đều như Hình 1a, sau đó Nam trải các mặt của chiếc hộp với các số đo đã cho như Hình 1b. Hãy cho biết:
a) Hình này có bao nhiêu mặt bên
b) Diện tích của mỗi mặt bên
c) Diện tích của tất cả các mặt bên
d) Diện tích đáy của hình này
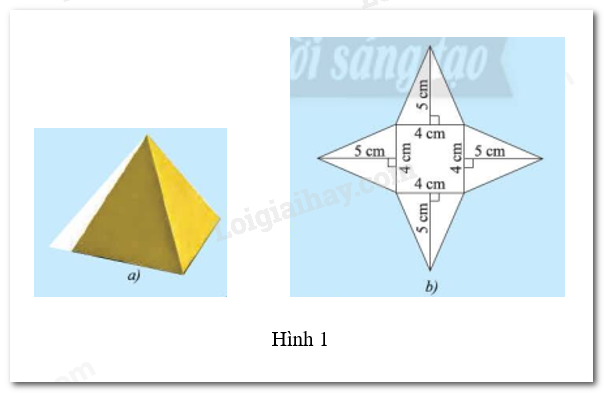
Sử dụng công thức tính diện tích các mặt bên (tam giác), đáy (hình vuông)
a) Hình này có 4 mặt bên
b) Diện tích của mỗi mặt bên là: \(4.5:2 = 10\) (\(c{m^2}\))
c) Diện tích của tất cả các mặt bên là: \(10.4 = 40\) (\(c{m^2}\))
d) Diện tích đáy là: \(4.4 = 16\) (\(c{m^2}\))

Các bài tập cùng chuyên đề
a) Tính diện tích xung quanh của mỗi hình chóp tứ giác đều dưới đây.
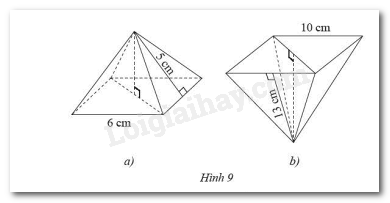
b) Cho biết chiều cao của hình chóp tứ giác đều trong Hình 9a và Hình 9b lần lượt là 4cm và \(12\)cm. Tính thể tích của mỗi hình.
Cho một hình chóp tứ giác đều có độ dài cạnh đáy bằng 10 cm và độ dài trung đoạn bằng 15 cm. Tính diện tích xung quanh của hình chóp tứ giác đều đó.
Cho hình chóp tứ giác đều S.ABCD có độ dài cạnh đáy bằng 7cm và độ dài trung đoạn bằng 10 cm. Tính diện tích xung quanh của hình chóp tứ giác đều đó
Một mái che giếng trời có dạng hình chóp tứ giác đều với độ dài cạnh đáy khoảng 2, 2 m và độ dài trung đoạn khoảng 2, 8 m (hình 20). Cần phải trả bao nhiêu tiền để làm mái che giếng trời? Biết rằng giá để làm mỗi mét vuông mái che được tính là 1 800 000 đồng.(bao gồm cả tiền vật liệu và tiền công)
Cho một hình chóp tứ giác đều có độ dài cạnh đáy là 10 cm và độ dài trung đoạn là 13 cm. Tính diện tích xung quanh của hình chóp tứ giác đều đó.
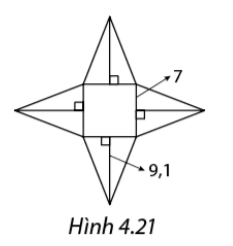
Tính diện tích xung quanh của hình chóp tứ giác đều có hình khai triển như Hình 4.21.
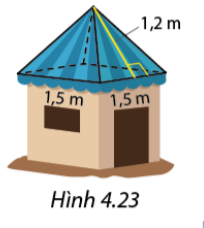
Mái của một chòi trên bãi biển có dạng hình chóp tứ giác đều như Hình 4.23. Tính diện tích vải bạt cần dùng để phủ mái chòi, biết rằng người ta chỉ dùng một lớp vải bạt (không tính phần viền xung quanh)\
Một hình chóp tứ giác đều có diện tích xung quanh \(36c{m^2}\) và đường cao của mặt bên kẻ từ đỉnh của hình chóp bằng \(6cm\). Tính diện tích đáy.
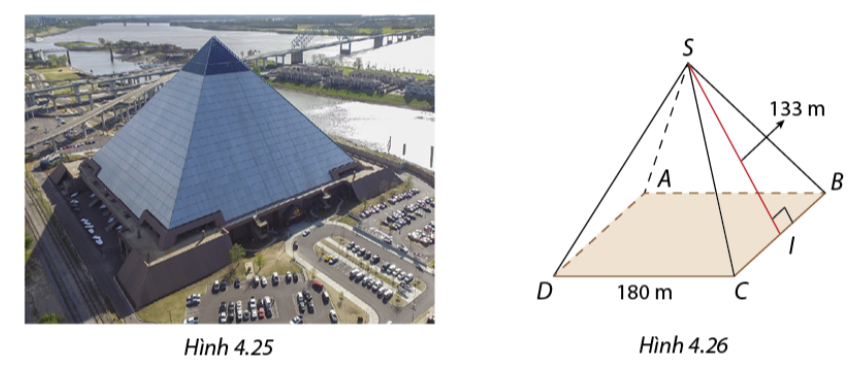
Đại kim tự tháp của Mĩ (Thẻ Great American Pyramid) nằm ở Memphis, bang Tennessee là một trong những kim tự tháp lớn nhất thế giới (Hình 4.25). Nơi đây hoạt động như một trung tâm thương mại và giải trí sầm uất. Đại kim tự tháp có dạng hình chóp tứ giác đều với đáy là hình vuông cạnh 180 m và chiều cao của mặt bên kẻ từ đỉnh hình chóp bằng 133m (Hình 4.26). Tính diện tích mặt ngoài của Đại kim tự tháp này.
Tính diện tích xung quanh của hình chóp tứ giác đều có hình khai triển như Hình 4.34.

Một mái che giếng trời có dạng hình chóp tứ giác đều (Hình 2) cạnh đáy 2,5m, chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tứ giác đều bằng 2,2m.
a) Tính diện tích xung quanh của mái che.
b) Chi phí cho mỗi mét vuông mái che bằng kính là 2 triệu đồng. Hỏi chi phí để hoàn thành mái che là bao nhiêu
Cho hình chóp tứ giác đều có diện tích xung quanh bằng \(192c{m^2}\) và độ dài trung đoạn bằng 8 cm. Tính độ dài cạnh đáy của hình chóp tứ giác đều đó.
Tính diện tích xung quanh của hình chóp tứ giác đều ở mỗi hình 11a; 11b;

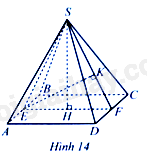
Cho hình chóp tứ giác đều \(S.ABCD\) có chiều cao \(SH\). Gọi \(E,F\) lần lượt là trung điểm của \(AB,CD\). Kẻ \(EK\) vuông góc với \(SF\) tại \(K\) (Hình 14). Biết \(AB = EF = 13cm,SH = EK\). Tính tổng diện tích các mặt của hình chóp tứ giác đều đó.
Tính diện tích xung quanh của hình chóp tứ giác đều ở mỗi hình 15a, 15b:

Bác Khôi làm một chiếc hộp gỗ có dạng hình chóp tứ giác đều với độ dài cạnh đáy của hình chóp là 2m, trung đoạn của hình chóp là 3 m. Bác Khôi muốn sơn bốn mặt xung quanh của hộp gỗ. Cứ mỗi mét vuông sơn cần trả 30 000 đồng (tiền sơn và tiền công). Hỏi bác Khôi phải trả chi phí là bao nhiêu
Một chiếc lều có dạng hình chóp tứ giác đều, cạnh đáy bằng 2 m, chiều cao bằng 2 m
a) Thể tích không khí trong lều là bao nhiêu?
b) Biết lều phủ vải bốn phía và cả mặt tiếp đất. Tính diện tích vải bạt cần dùng (coi mép nối không đáng kể), biết rằng người ta đo chiều cao của mặt bên xuất phát từ đỉnh của chiếc lều là 2,24m.
Một hình chóp tứ giác đều có độ dài trung đoạn là \(a\), diện tích xung quanh là \(S_{xq}\) thì có độ dài cạnh đáy là
-
A.
\(\frac{{{S_{xq}}}}{a}\);
-
B.
\(\frac{{2{S_{xq}}}}{a}\)
-
C.
\(\frac{{{S_{xq}}}}{2a}\)
-
D.
\(\frac{{{S_{xq}}}}{4a}\)

Cho hình chóp tứ giác đều có chiều cao \(10 \ cm\), cạnh đáy \(48 \ cm\). Tính diện tích xung quanh của hình chóp đó.
a) Một máy bay đang chuẩn bị hạ cánh xuống vị trí điểm B. Cơ trưởng tính toán rằng quãng đường AB máy bay bay từ vị trí A đến vị trí hạ cánh tại điểm B là 38 km. Hãy tính độ cao AC của máy bay trước khi hạ cánh, biết rằng lúc đó máy bay cách điểm hạ cánh một khoảng CB = 37 km. (Kết quả làm tròn 2 chữ số thập phân)
b) Một hình chóp tứ giác đều có độ dài cạnh đáy là 10 cm và chiều cao của mặt bên là 8 cm. Tính diện tích xung quanh của hình chóp.
Cho một hình chóp tứ giác đều có độ dài cạnh đáy bằng 8cm và độ dài trung đoạn bằng 15cm. Diện tích xung quanh của hình chóp tứ giác đều đó là:
-
A.
\(960c{m^2}\).
-
B.
\(240c{m^2}\).
-
C.
\(480c{m^2}\).
-
D.
\(150c{m^2}\).
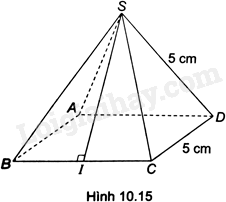
Tính diện tích xung quanh của hình chóp tứ giác đều S.ABCD trong Hình 10.15. Biết $\sqrt{18,75}\approx 4,3$
Một hình chóp tứ giác đều có cạnh đáy bằng 15cm, độ dài trung đoạn bằng 10cm. Diện tích giấy dán kính bốn mặt bên của đèn lồng là (coi như mép dán không đáng kể) là:
A. \(200c{m^2}\)
B. \(300c{m^2}\)
C. \(400c{m^2}\)
D. \(500c{m^2}\)
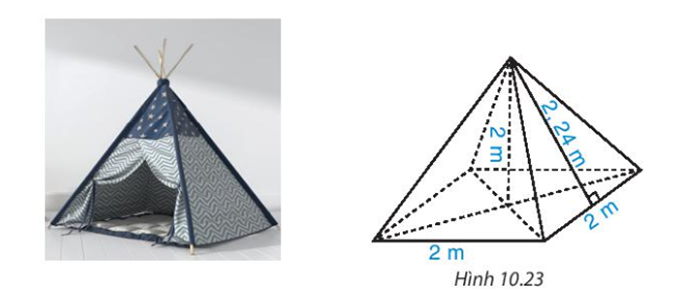
Một khối đồ chơi làm bằng gỗ được tạo thành từ hai hình chóp tứ giác đều. Cạnh đáy của mỗi hình chóp tứ giác đều bằng 6cm, trung đoạn của nó bằng 4cm (H.10.23). Người ta sơn mặt ngoài của món đồ chơi. Hỏi diện tích cần sơn bằng bao nhiêu centimét vuông?

Diện tích xung quanh của hình chóp tứ giác đều bằng:
A. Tích chu vi đáy với độ dài trung đoạn của nó.
B. \(\frac{1}{3}\) tích của diện tích đáy với chiều cao của nó.
C. Tích của nửa chu vi đáy với trung đoạn của nó.
D. Nửa tích của diện tích đáy với trung đoạn của nó.
Một hình chóp tứ giác đều có diện tích đáy bằng 36 cm2, độ dài trung đoạn bằng 4 cm.
Diện tích xung quanh của hình chóp tứ giác đều này bằng:
A. 144 cm2.
B. 48 cm2.
C. 9 cm2.
D. 40 cm2.
Bạn Khôi dự định làm một chiếc đèn lồng hình chóp tứ giác đều có độ dài cạnh đáy và đường cao của mặt bên tương ứng với cạnh đáy lần lượt là 40cm và 30cm. Em hãy tính giúp Khôi xem cần phải dùng bao nhiêu mét vuông giấy vừa đủ để dán tất cả các mặt bên của chiếc đèn lồng? Biết rằng nếp gấp không đáng kể.
Bạn Xuân dự định làm một chiếc đèn lồng treo có hình dạng là hai hình chóp tứ giác đều bằng nhau ghép lại như hình 10.26. Cạnh đáy của mỗi hình chóp tứ giác đều bằng 120 cm, các cạnh bên bằng 100 cm. Bạn Xuân cần dùng bao nhiêu mét vuông giấy để dán các mặt của chiếc đèn lồng này? (coi mép dán là không đáng kể).
Một hình chóp tứ giác đều có thể tích bằng \(50c{m^3}\), chiều cao hình chóp bằng 6cm, chiều cao mặt bên bằng 4cm. Tính diện tích xung quanh hình chóp đó.
-
A.
\(40(c{m^2})\)
-
B.
\(50(c{m^2})\)
-
C.
\(60(c{m^2})\)
-
D.
\(80(c{m^2})\)







Danh sách bình luận