Tấm bìa nào sau đây có thể gấp thành hình chóp tứ giác đều
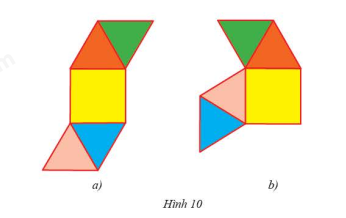
- Trên một tấm bìa, vẽ một hình vuông và 4 hình tam giác cân như hình 10a, 10b
- Gấp hai hình lại rồi tìm hình chóp tứ giác đều
- Trên một tấm bìa, vẽ một hình vuông và 4 hình tam giác cân như hình 10a, 10b
- Gấp hai hình lại ta thấy tấm bìa Hình 10a có thể gấp thành hình chóp tứ giác đều?

Các bài tập cùng chuyên đề
Trong các tấm bìa bên dưới, có mấy hình gấp lại được thành hình chóp tứ giác đều
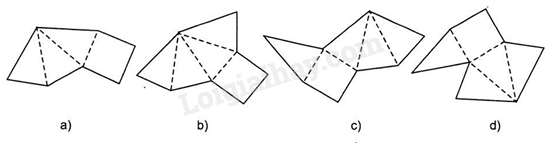
-
A.
1.
-
B.
2.
-
C.
3.
-
D.
4.
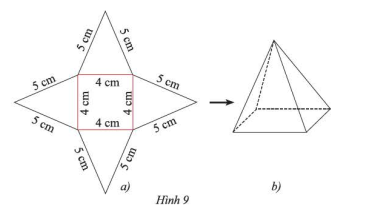
Tạo lập hình chóp tứ giác đều có độ dài cạnh đáy 4cm và cạnh bên 5cm theo hướng dẫn sau:
- Trên một tấm bìa, vẽ một hình vuông và bốn hình tam giác cân với kích thước như Hình 9a.
- Cắt tấm bìa như hình vẽ, rồi gấp theo các đường màu đỏ ta được hình chóp tứ giác đều như Hình 9b.
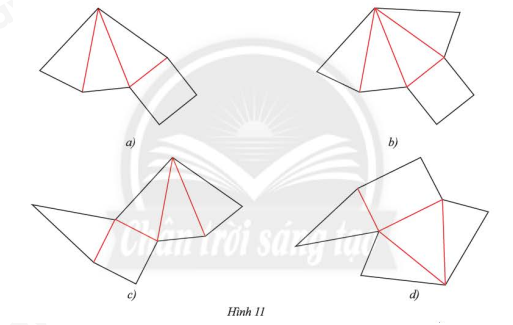
Trong các tấm bìa dưới đây, tấm bìa nào gấp theo đường màu đỏ thì được một hình chóp tứ giác đều?
Chị Hà dự định gấp một hộp quà từ tấm bìa như Hình 12. Cái hộp mà chị Hà dự định gấp có dạng hình gì?

Thực hiện theo các hoạt động sau:
a) Vẽ trên giấy (hay bìa mỏng) 1 hình vuông và 4 hình tam giác với các cạnh và vị trí như hình 12
b) Cắt rời theo đường viền (màu đỏ) của hình vừa vẽ (phần tô màu) và gấp lại để được hình chóp tứ giác đều như hình 13.
c) Quan sát hình chóp tứ giác đều ở hình 13 và nêu số mặt, số cạnh của hình chóp tứ giác đều đó
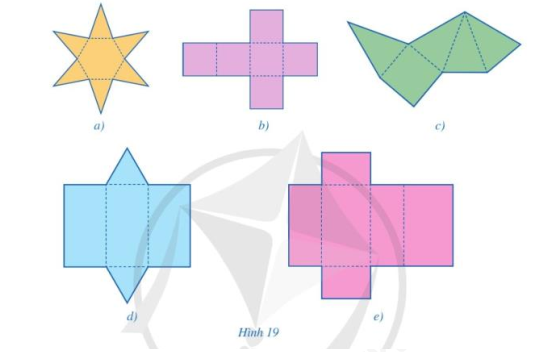
Trong các miếng bìa ở hình 19a, 19b, 19c, 19d, miếng bìa nào có thể gấp lại (theo các nét đứt) để được hình chóp tứ giác đều?
Trong hình 4.14, hình nào là hình khai triển của hình chóp tứ giác đều?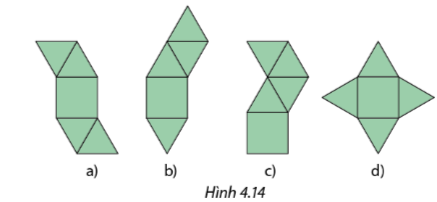
Tạo lập hình chóp tứ giác đều có cạnh đáy bằng 4cm, chiều cao của mặt bên xuất phát từ đỉnh của hình chóp tứ giác đều bằng 5cm.
Trong các miếng bìa ở Hình 10.25, hình nào gấp lại cho ta một hình chóp tứ giác đều?

Từ tờ giấy cắt ra một hình vuông rồi thực hiện các thao tác như hình 10.26 để có thể ghép được các mặt bên của hình chóp tứ giác đều.

Cho hình bên, độ dài cạnh bên của hình là:
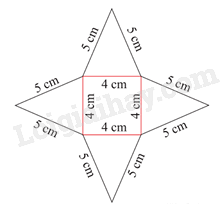
-
A.
5cm.
-
B.
4cm.
-
C.
16cm.
-
D.
10cm.








Danh sách bình luận