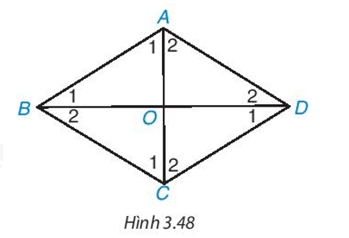
Cho hình thoi ABCD có hai đường chéo AC, BD cắt nhau tại O (H.3.48).
a) ∆ABD có cân tại A không?
b) AC có vuông góc với BD không và AC có là đường phân giác của góc A không? Vì sao?
Dựa vào định nghĩa hình thoi.
a) Vì tứ giác ABCD là hình thoi nên AB = AD.
Suy ra ∆ABD có cân tại A.
b) Vì tứ giác ABCD là hình thoi nên AB = BC = CD = DA.
Xét ∆ABC và ∆ADC có:
AB = AD (chứng minh trên);
BC = CD (chứng minh trên);
Cạnh AC chung.
Do đó ∆ABC = ∆ADC (c.c.c)
Suy ra \(\)\(\widehat {{A_1}} = \widehat {{A_2}}\)(hai góc tương ứng)
Hay AC là đường phân giác của góc A.
Tam giác ABD cân tại A có AO là đường phân giác của góc A (vì AC là đường phân giác góc A) nên AO cũng là đường cao.
Khi đó AO ⊥ BD hay AC ⊥ BD.
Vậy AC vuông góc với BD và AC là đường phân giác của góc A.

Các bài tập cùng chuyên đề
Hình 11a là hình chụp tấm lưới thép được đan thành nhiều mắt. Hình 11b là hình vẽ phóng to của một mắt lưới. Đo độ dài các cạnh của tứ giác \(ABCD\) và rút ra nhận xét.

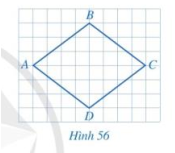
So sánh độ dài các cạnh của tứ giác ABCD ở hình 56
Từ định nghĩa và tính chất của hình bình hành, ta có thể suy ra tính chất nào về cạnh, góc và đường chéo của hình thoi \(ABCD\)?







Danh sách bình luận