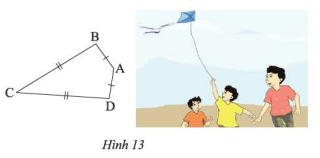
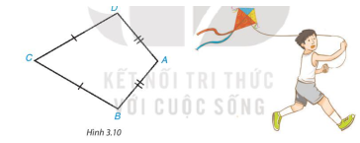
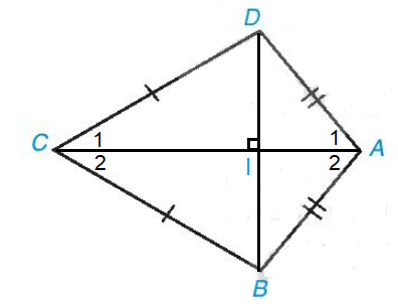
Tứ giác ABCD trong Hình 3.10 có AB = AD, CB = CD, được gọi là hình “cái diều”.
a) Chứng minh rằng AC là đường trung trực của đoạn thẳng BD.
b) Tính các góc B, D biết rằng \(\widehat A\)=100°,\(\widehat C\)=60°
Áp dụng định lí tổng các góc trong một tứ giác bằng \(360^0\)
a) Nối AC, BD (như hình vẽ
Ta có AB = AD hay hai điểm A cách đều hai đầu mút B và D;
CB = CD hay hai điểm C cách đều hai đầu mút B và D;
Do đó, hai điểm A và C cách đều hai đầu mút B và D.
Vậy AC là đường trung trực của đoạn thẳng BD.
b) Gọi I là giao điểm của AC và BD.
Vì AC là đường trung trực của đoạn thẳng BD nên AC ⊥ BD.
• Xét tam giác ABD cân tại A (vì AB = AD) có AI là đường cao (vì AI ⊥ BD)
Nên AI cũng là tia phân giác của \(\widehat {BA{\rm{D}}}\) hay \(\widehat {{A_1}} = \widehat {{A_2}}\)
Suy ra \(\widehat {{A_1}} = \widehat {{A_2}} = \widehat {B{\rm{D}}A}:2 = {100^o}:2 = {50^o}\)
• Xét tam giác BCD cân tại C (vì BC = CD) có CI là đường cao (vì AC ⊥ BD)
Nên CI cũng là tia phân giác của \(\widehat {BC{\rm{D}}}\) hay \(\widehat {{C_1}} = \widehat {{C_2}}\)
Suy ra \(\widehat {{C_1}} = \widehat {{C_2}} = \widehat {BC{\rm{D}}}:2 = {60^o}:2 = {30^o}\)
• Xét tam giác ACD có: \(\widehat {{A_1}} + \widehat {{C_1}} + \widehat {A{\rm{D}}C} = {180^o}\) (định lí tổng ba góc trong một tam giác).
Hay 50°+30°+\(\widehat {A{\rm{D}}C}\)=180°
Suy ra \(\widehat {A{\rm{D}}C}\)=180°−50°−30°=100°
Xét tứ giác ABCD có:
\(\widehat {BA{\rm{D}}} + \widehat {ABC} + \widehat {BC{\rm{D}}} + \widehat {A{\rm{D}}C} = {360^o}\)(định lí tổng bốn góc của một tứ giác).
Hay 100°+\(\widehat {ABC}\)+60°+100°=360°
Suy ra \(\widehat {ABC}\)+260°=360o
Do đó \(\widehat {ABC}\)=360°−260°=100o
Vậy \(\widehat {ABC}\)=100° ;\(\widehat {A{\rm{D}}C}\)=100°

Các bài tập cùng chuyên đề
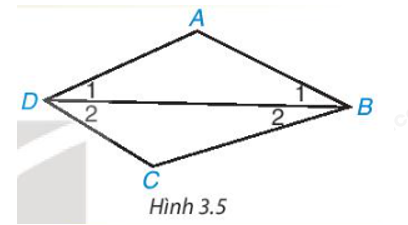
Cho tứ giác ABCD. Kẻ đường chéo BD (H.3.5). Vận dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD, tính tổng các góc của tứ giác ABCD.
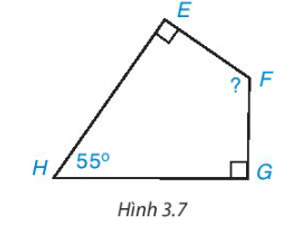
Cho tứ giác EFGH như Hình 3.7. Hãy tính góc F.
Câu hỏi mở đầu
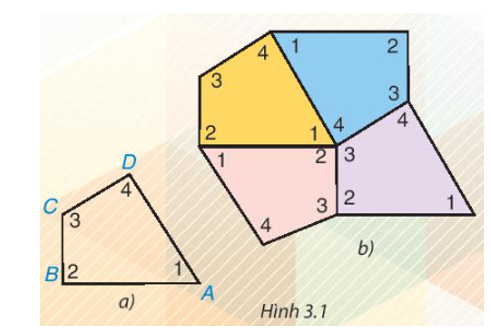
Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong Hình 3.1a. Ghép bốn tứ giác giấy đó để được hình như Hình 3.1b.
- Em có thể ghép bốn tứ giác khít nhau như vậy không?
- Em có nhận xét gì về bốn góc tại điểm chung của bốn tứ giác? Hãy cho biết tổng số đo.
Trong một tứ giác, hỏi số góc tù nhiều nhất là bao nhiêu và số góc nhọn nhiều nhất là bao nhiêu? Vì sao?
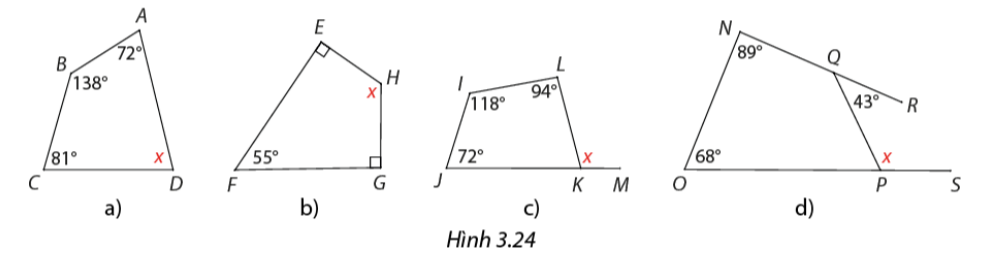
Tính góc chưa biết của các tứ giác trong Hình 3.8.
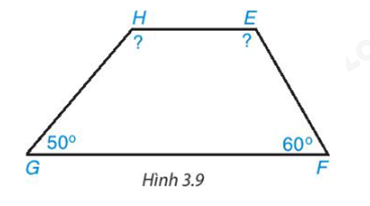
Tính góc chưa biết của tứ giác trong Hình 3.9. Biết rằng \(\widehat H\)=\(\widehat E\)+10o
Tính số đo các góc của tứ giác ABCD trong Hình 3.26.
Cho hình thang cân ABCD (AB // CD) có AB = AD. Biết \(\widehat {AB{\rm{D}}} = {30^o}\), tính số đo các góc của hình thang đó.
Trong các khẳng định sau, khẳng định nào đúng?
A. Không có tứ giác nào mà không có góc tù.
B. Nếu tứ giác có ba góc nhọn thì góc còn lại là góc tù.
C. Nếu tứ giác có hai góc tù thì góc còn lại phải nhọn.
D. Không có tứ giác nào có ba góc tù.
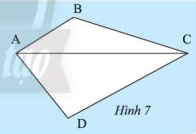
Đường chéo \(AC\) chia tứ giác \(ABCD\) thành hai tam giác \(ACB\) và \(ACD\) (Hình 7). Tính tổng các góc của tam giác \(ACB\) và tam giác \(ACD\). Từ đó, ta có nhận xét gì về tổng các góc của tứ giác \(ABCD\) .
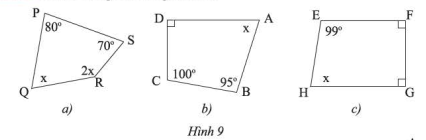
Tìm \(x\) trong mỗi tứ giác sau:
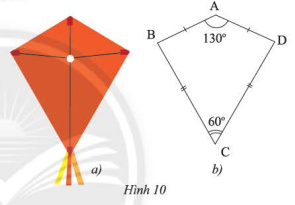
Phần thân của cái diều ở Hình 10a được vẽ lại như Hình 10b. Tìm số đo các góc chưa biết trong hình.
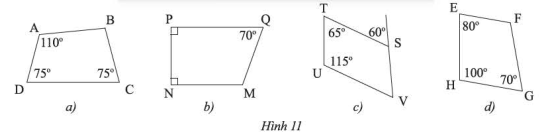
Tìm số đo các góc chưa biết của các tứ giác trong Hình 11.
Góc kề bù với một góc của tứ giác được gọi là góc ngoài của tứ giác đó.
Hãy tính tổng số đo bốn góc ngoài \(\widehat {{A_1}};\;\widehat {{B_1}};\;\widehat {{C_1}};\;\widehat {{D_1}}\) của tứ giác \(ABCD\) ở hình 12.

Tứ giác \(ABCD\) có \(\widehat A = 100^\circ \), góc ngoài tại đỉnh \(B\) bằng \(110^\circ \), \(\widehat C = 75^\circ \). Tính số đo góc \(D\)
Tứ giác \(ABCD\) có góc ngoài tại đỉnh \(A\) bằng \(65^\circ \), góc ngoài tại đỉnh \(B\) bằng \(100^\circ \), góc ngoài tại đỉnh \(C\) bằng \(60^\circ \). Tính số đo góc ngoài tại đỉnh \(D\).
Tứ giác \(ABCD\) có số đo \(\widehat A = x;\;\widehat B = 2x;\;\widehat C = 3x;\;\widehat D = 4x\). Tính số đo các góc của tứ giác đó.
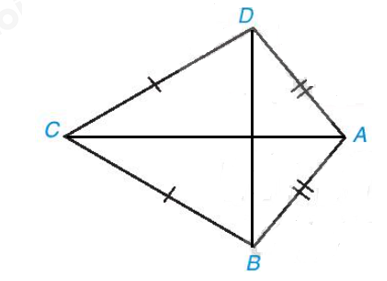
Ta gọi tứ giác ABCD với AB = AD, CB = CD (hình 13) là hình “cái diều”.
a. Chứng minh rằng AC là đường trung trực của BD.
b. Cho biết \(\widehat B = {95^0},\widehat C = {35^0}.\)Tính \(\widehat A\) và \(\widehat D\)
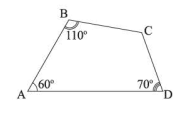
Cho tứ giác \(ABCD\), biết \(\widehat A = 60^\circ ;\;\widehat B = 110^\circ ;\;\widehat D = 70^\circ \). Khi đó số đo góc \(C\) là:
A. \(120^\circ \)
B. \(110^\circ \)
C. \(130^\circ \)
D. \(80^\circ \)
Hình ảnh thửa ruộng nhìn từ trên cao hay hình ảnh cánh diều (Hình 12) gợi lên những hình tứ giác.
Tứ giác là hình có những tính chất gì?
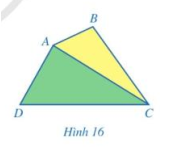
Quan sát tứ giác ABCD ở Hình 16, đường chéo AC chia nó thành hai tam giác ABC và ACD.
a) Gọi T1 và T2 lần lượt là tổng các góc của tam giác ABC và tam giác ACD. Tổng T1 + T2 bằng bao nhiêu độ?
b) Gọi T là tổng các góc của tứ giác ABCD. So sánh T với T1 + T2.
Tìm x trong hình 18
a) Tứ giác ABCD có \(\widehat A + \widehat B = {180^o}\) thì \(\widehat B + \widehat D\) bằng bao nhiêu độ?
b) Có hay không một tứ giác có 2 góc tù và 2 góc vuông?
c) Có hay không một tứ giác có cả 4 góc đều là góc nhọn?
Cho tứ giác ABCD có \(\widehat A = {60^o},\widehat B = {70^o},\widehat C = {80^o}\). Khi đó, \(\widehat D\) bằng:
A. 130o
B. 140o
C. 150o
D. 160o
- Vẽ hai tứ giác bất kì. Đo và tính tổng các góc của mỗi tứ giác. Em có nhận xét gì về hai tổng này?
- So sánh tổng các góc của tứ giác \(ABCD\) với tổng các góc của hai tam giác \(ABD\) và \(BCD\), từ đó tính tổng các góc của tứ giác \(ABCD\)
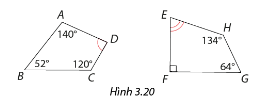
Tính số đo góc D và góc E của các tứ giác trong Hình 3.20.
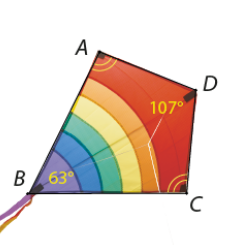
Cánh diều hình tứ giác \(ABCD\) có \(\widehat D = 107^\circ ,\widehat B = 63^\circ \) và \(\widehat A = \widehat C\) (Hình 3.21). Tính số đo góc A và góc C của cánh diều.
Tìm số đo x trong mỗi trường hợp ở Hình 3.24.
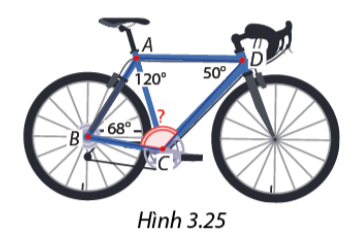
Khung xe đạp có dạng hình tứ giác \(ABCD\) như trong Hình 3.25 có \(\widehat {BAD} = 120^\circ ,\widehat B = 68^\circ ,\widehat D = 50^\circ \). Tính số đo góc \(BCD\).
Tứ giác \(ABCD\) có \(\widehat A = 108^\circ \) và \(\widehat B = \widehat C = \widehat D\). Tính số đo góc \(B\).











Danh sách bình luận