Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật. Chứng minh rằng: \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \).
Sử dụng kiến thức về quy tắc ba điểm để chứng minh: Nếu A, B, C là ba điểm bất kì thì \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Sử dụng quy tắc hình bình hành để chứng minh: Nếu ABCD là hình bình hành thì \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Sử dụng kiến thức về hai vectơ bằng nhau để chứng minh: Hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) được gọi là bằng nhau, kí hiệu \(\overrightarrow a = \overrightarrow b \) nếu chúng có cùng độ dài và cùng hướng.

Gọi O là tâm hình chữ nhật ABCD. Khi đó, O là trung điểm của AC, BD.
Suy ra \(\overrightarrow {OC} = - \overrightarrow {OA} ,\overrightarrow {OD} = - \overrightarrow {OB} \)
Ta có: \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SO} + \overrightarrow {OA} + \overrightarrow {SO} + \overrightarrow {OC} = 2\overrightarrow {SO} + \left( {\overrightarrow {OA} - \overrightarrow {OA} } \right) = 2\overrightarrow {SO} \)
\(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SO} + \overrightarrow {OB} + \overrightarrow {SO} + \overrightarrow {OD} = 2\overrightarrow {SO} + \left( {\overrightarrow {OB} - \overrightarrow {OB} } \right) = 2\overrightarrow {SO} \)
Do đó: \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \).

Các bài tập cùng chuyên đề
Trong Ví dụ 6, chứng minh rằng:
a) \(\overrightarrow {BN} \) và \(\overrightarrow {DM} \) là hai vectơ đối nhau;
b) \(\overrightarrow {SD} - \overrightarrow {BN} - \overrightarrow {CM} = \overrightarrow {SC} \)
Cho hình hộp hình chữ nhật ABCD.A’B’C’D’. Chứng minh rằng \(\overrightarrow {BB'} + \overrightarrow {CD} + \overrightarrow {AD} = \overrightarrow {BD'} \)
Trong Hình 2.14, hãy phát biểu quy tắc hình hộp với các vectơ có điểm đầu là B.
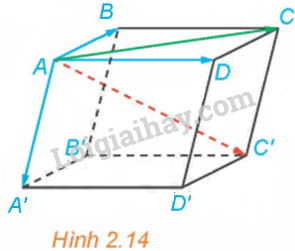
Cho hình hộp ABCD.A’B’C’D’ (H.2.14).

a) Hai vectơ \(\overrightarrow {AB} + \overrightarrow {AD} \) và \(\overrightarrow {AC} \) có bằng nhau hay không?
b) Hai vectơ \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \) và \(\overrightarrow {AC'} \) có bằng nhau hay không?
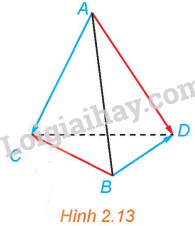
Cho tứ diện ABCD (H.2.13). Chứng minh rằng \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} + \overrightarrow {CB} \).
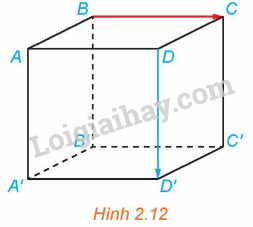
Trong Ví dụ 3, hãy tính độ dài của vectơ \(\overrightarrow {AC} + \overrightarrow {C'D'} \).
Ví dụ 3: Cho hình lập phương ABCD.A’B’C’D’ có độ dài mỗi cạnh bằng 1 (H.2.12).
Trong không gian, cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khác \(\overrightarrow 0 \). Lấy điểm O và vẽ các vectơ\(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \). Lấy điểm O’ khác O và vẽ các vectơ \(\overrightarrow {O'A'} = \overrightarrow a ,\overrightarrow {O'B'} = \overrightarrow b \) (H.2.21).

a) Hãy giải thích vì sao \(\overrightarrow {AB} = \overrightarrow {A'B'} \).
b) Áp dụng định lí côsin cho hai tam giác OAB và O’A’B’ để giải thích vì sao \(\widehat {AOB} = \widehat {A'O'B'}\)
Cho tứ diện ABCD. Chứng minh rằng:
a) \(\overrightarrow {AB} .\overrightarrow {CD} = \overrightarrow {AC} .\overrightarrow {CD} + \overrightarrow {BC} .\overrightarrow {DC} \);
b) \(\overrightarrow {AB} .\overrightarrow {CD} + \overrightarrow {AC} .\overrightarrow {DB} + \overrightarrow {AD} .\overrightarrow {BC} = 0\).
Ba sợi dây không giãn với khối lượng không đáng kể được buộc chung một đầu và được kéo căng về ba hướng khác nhau (H.2.31). Nếu các lực kéo làm cho ba sợi dây ở trạng thái đứng yên thì khi đó ba sợi dây nằm trên cùng một mặt phẳng. Hãy giải thích vì sao.

Cho hình chóp tứ giác S. ABCD. Chứng minh rằng tứ giác ABCD là hình bình hành nếu và chỉ nếu \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \).
Cho hình lăng trụ tam giác ABC.A’B’C’ có \(\overrightarrow {AA'} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b \) và \(\overrightarrow {AC} = \overrightarrow c \). Hãy biểu diễn các vectơ sau qua các vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \):
a) \(\overrightarrow {AB'} \);
b) \(\overrightarrow {B'C} \);
c) \(\overrightarrow {BC'} \).
Cho hình hộp ABCD.A’B’C’D’. Chứng minh rằng:
a) \(\overrightarrow {AB} + \overrightarrow {DD'} + \overrightarrow {C'D'} = \overrightarrow {CC'} \);
b) \(\overrightarrow {AB} + \overrightarrow {CD'} - \overrightarrow {CC'} = \overrightarrow 0 \);
c) \(\overrightarrow {BC} - \overrightarrow {CC'} + \overrightarrow {DC} = \overrightarrow {A'C} \)
Cho tứ diện ABCD, lấy hai điểm M, N thỏa mãn \(\overrightarrow {MB} + 2\overrightarrow {MA} = \overrightarrow 0 \) và \(\overrightarrow {NC} = 2\overrightarrow {DN} \). Hãy biểu diễn \(\overrightarrow {MN} \) theo \(\overrightarrow {AD} \) và \(\overrightarrow {BC} \).
Cho tứ diện ABCD, gọi G là trọng tâm của tam giác BCD và M là trung điểm của đoạn thẳng AG. Khi đó \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} \) bằng
A. \(\overrightarrow {MG} \).
B. \(2\overrightarrow {MG} \).
C. \(3\overrightarrow {MG} \).
D. \(4\overrightarrow {MG} \).
Trong không gian , cho hai vecto\(\;\vec a,\vec b.\;\) Lấy một điểm M tùy ý
a) Vẽ \(\overrightarrow {MA} = \vec a,\;\overrightarrow {MB} = \vec b\;,\overrightarrow {MC} = \overrightarrow { - b} \)
b) Tổng của hai vecto \(\vec a\;\)và \(\;\overrightarrow { - b} \) bằng vecto nào trong hình 7

Cho hình hộp ABCD.A’B’C’D’. Tìm liên hệ giữa \(\overrightarrow {AB} + \overrightarrow {AD} \) và \(\overrightarrow {AC} ;\;\overrightarrow {AC} + \overrightarrow {AA'} \) và \(\overrightarrow {AC'} \)

Trong không gian, cho 2 vec tơ \(\vec a\)và\(\vec b\) . Lấy một điểm A tùy ý.
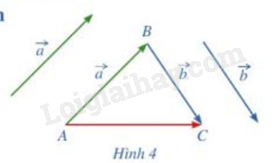
a) Vẽ \(\overrightarrow {AB} \)\( = \vec a\),\(\overrightarrow {BC} \)\( = \vec b\)
b) Tổng của 2 vec tơ \(\vec a\)và\(\vec b\) bằng vec tơ nào trong hình 4?
Cho hình hộp ABCD. A’B’C’D’. Vecto \(\vec u = \overrightarrow {AA'} + \overrightarrow {A'B'} + \overrightarrow {A'D'} \) bằng vecto nào dưới đây?
A. \(\overrightarrow {A'C}\)
B. \(\overrightarrow {CA'} \)
C. \(\overrightarrow {AC'} \)
D. \(\overrightarrow {C'A} \)
Cho tứ diện ABCD. Chứng minh rằng:
a, \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AD} + \overrightarrow {BC} \)
b, \(\overrightarrow {AB} - \overrightarrow {CD} = \overrightarrow {AC} + \overrightarrow {DB} \)
Cho hình hộp ABCD.A’B’C’D’. Gọi G là trọng tâm tam giác AB’D’.Chứng minh rằng \(\overrightarrow {A'C} = 3\overrightarrow {A'G} \)
Một chiếc oto được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình chữ nhật ABCD, mặt phẳng (ABCD) song song với mặt phẳng nằm ngang . Khung sắt có được buộc vào móc E của chiếc cần cẩu sao cho các đoạn dây cáp EA, EB, EC, ED có độ dài bằng nhau và cùng tạo với mặt phẳng (ABCD) một góc bằng 60\(^\circ \) (hình 16). Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Tính trọng lượng của chiếc xe oto (làm tròn đến hàng đơn vị), biết rằng các lực căng \(\overrightarrow {{F_1},} \overrightarrow {{F_2},} \overrightarrow {{F_3},} \overrightarrow {{F_4}} \) đều có cường độ là 4700N và trọng lượng của khung sắt là 3000N.

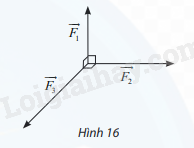
Ba lực \(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} ;\overrightarrow {{F_3}} \) cùng tác động vào một vật có phương đôi một vuông góc và có độ lớn lần lượt là 2N; 3N; 4N (Hình 16). Tính độ lớn hợp lực của ba lực đã cho.
Cho hình lập phương ABCD. A′B′C′D′ có cạnh bằng đơn vị. Tìm độ dài các vectơ sau đây:
a) \(\overrightarrow a = \overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} \)
b) \(\overrightarrow b = \overrightarrow {BC} - \overrightarrow {BA} + \overrightarrow {C'A} \)
Cho tứ diện ABCD có M và N lần lượt là trung điểm của AB và CD. Hãy thực hiện các phép toán sau đây:
a) \(\overrightarrow {BM} + \overrightarrow {AC} + \overrightarrow {ND} \)
b) \(\overrightarrow {AD} - \overrightarrow {AM} + \overrightarrow {NC} \)
Cho hình chóp S.ABCD có đáy là hình bình hành. Tìm các vectơ hiệu \(\overrightarrow {AS} - \overrightarrow {DC} ,\overrightarrow {CS} - \overrightarrow {DA} \)
Cho hình hộp ABCD.EFGH. Thực hiện các phép toán sau đây:
a) \(\overrightarrow {DA} + \overrightarrow {DC} + \overrightarrow {DH} \)
b) \(\overrightarrow {HE} + \overrightarrow {GC} + \overrightarrow {AB} \)
Cho hình hộp ABCD.A′B′C′D′.
a) Tìm các vectơ tổng \(\overrightarrow {AB} + \overrightarrow {AD} \), \(\overrightarrow {AC} + \overrightarrow {AA'} \)
b) Dùng kết quả của câu a và tính chất kết hợp của phép cộng vectơ để chứng minh \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC} \)
Cho hình hộp ABCD.A′B′C′D′ (Hình 5).
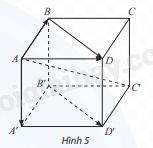
a) Trong mặt phẳng (ABCD), tìm vectơ tổng \(\overrightarrow {AB} + \overrightarrow {AD} \)
b) So sánh hai vectơ \(\overrightarrow {BD'} ,\overrightarrow {B'D'} \)
c) Giải thích tại sao \(\overrightarrow {AB} + \overrightarrow {B'D'} = \overrightarrow {AD} \).
Cho hình hộp ABCD.A′B′C′D′. Chứng minh rằng:
a) \(\overrightarrow {AB} + \overrightarrow {B'C'} + \overrightarrow {DD'} = \overrightarrow {AC'} \);
b) \(\overrightarrow {DB'} + \overrightarrow {D'D} + \overrightarrow {BD'} = \overrightarrow {BB'} \);
c) \(\overrightarrow {AC} + \overrightarrow {BA'} + \overrightarrow {DB} + \overrightarrow {C'D} = \overrightarrow 0 \).
Cho hình bình hành ABCD. Gọi S là một điểm không thuộc mặt phẳng chứa hình bình hành. Chứng minh rằng \(\overrightarrow {SA} + \overrightarrow {SC} = \overrightarrow {SB} + \overrightarrow {SD} \)







Danh sách bình luận