Cho đường tròn (O; R). Từ điểm M nằm ngoài đường tròn với \(MO = 2R\), vẽ hai tiếp tuyến tiếp xúc (O) tại A và B. Viết công thức tính phần diện tích nằm ngoài đường tròn (O) của tứ giác MAOB theo R.
+ Tính số đo góc AOM, từ đó tính được góc AOB, từ đó tính được số đo cung nhỏ AB.
+ Chứng minh \(\Delta OAM = \Delta OBM\left( {c.g.c} \right)\), suy ra \({S_{\Delta OAM}} = {S_{\Delta OBM}}\) nên \({S_{OAMB}} = {S_{\Delta OAM}} + {S_{\Delta OBM}} = 2{S_{\Delta OAM}}\).
+ Diện tích hình quạt tâm O, cung nhỏ AB là: ${{S}_{q}}=\frac{\pi .O{{A}^{2}}.sđ{{\overset\frown{AB}}_{nhỏ}}}{{{360}^{o}}}$.
+ Diện tích nằm ngoài đường tròn (O) của tứ giác MAOB là: \(S = {S_{OAMB}} - {S_q}\).
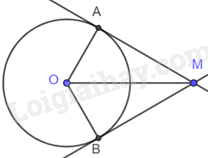
Vì MA, MB là tiếp tuyến của (O) nên
+ \(MA = MB\).
+ OA là tia phân giác của góc AOB, suy ra \(\widehat {AOM} = \widehat {MOB} = \frac{1}{2}\widehat {AOB}\).
Vì MA là tiếp tuyến của (O) nên \(MA \bot AO\) nên \(\Delta AOM\) vuông tại A. Suy ra:
+ \(AM = \sqrt {M{O^2} - A{O^2}} = \sqrt {{{\left( {2R} \right)}^2} - {R^2}} = \sqrt 3 R\).
+ \(\cos AOM = \frac{{OA}}{{OM}} = \frac{R}{{2R}} = \frac{1}{2}\) nên \(\widehat {AOM} = {60^o}\), suy ra \(\widehat {AOB} = {2.60^o} = {120^o}\).
Vì AOB là góc ở tâm chắn cung nhỏ AB nên số đo cung nhỏ AB bằng 120 độ.
Vì tam giác AOM vuông tại A nên
\({S_{AOM}} = \frac{1}{2}OA.AM = \frac{1}{2}.R.R\sqrt 3 = \frac{{{R^2}\sqrt 3 }}{3}\).
Tam giác OAM và tam giác OBM có:
\(OA = OB\) (= bán kính (O)),
\(OM\) chung,
\(\widehat {AOM} = \widehat {MOB}\left( {cmt} \right)\)
Do đó, \(\Delta OAM = \Delta OBM\left( {c.g.c} \right)\).
Suy ra, \({S_{OAMB}} = {S_{\Delta OAM}} + {S_{\Delta OBM}} = 2{S_{\Delta OAM}} = \frac{{2{R^2}\sqrt 3 }}{3}\).
Diện tích hình quạt tâm O, cung nhỏ AB là:
${{S}_{q}}=\frac{\pi .O{{A}^{2}}.sđ{{\overset\frown{AB}}_{nhỏ}}}{360}=\frac{\pi .{{R}^{2}}.120}{360}=\frac{\pi .{{R}^{2}}}{3}$.
Diện tích nằm ngoài đường tròn (O) của tứ giác MAOB là: \(S = {S_{OAMB}} - {S_q} = \frac{{2{R^2}\sqrt 3 }}{3} - \frac{{\pi .{R^2}}}{3} = \frac{{{R^2}}}{3}\left( {2\sqrt 3 - \pi } \right)\).

Các bài tập cùng chuyên đề
Để mô phỏng nguyệt thực, hãy cắt hai hình tròn từ giấy: hình tròn thứ nhất màu sáng tượng trưng cho Mặt Trăng, hình tròn thứ hai màu tối (to hơn bằng giấy mờ càng tốt) tượng trưng cho bóng Trái Đất. Sắp xếp hai hình tròn để:
a) Mô phỏng nguyệt thực một phần. Khi đó, hình ảnh của hai đường tròn có vị trí tương đối như thế nào?
b) Mô phỏng nguyệt thực toàn phần. Khi đó, hình ảnh của hai đường tròn có vị trí tương đối như thế nào?
Tròn cho rằng: Nói “hai đường tròn không cắt nhau” cũng có nghĩa là “hai đường tròn không giao nhau”. Theo em, Tròn đúng hay sai?
Hình 5.37 cho thấy hình ảnh của những đường tròn qua cách trình bày một số sản phẩm mây tre đan. Bằng cách đánh số các đường tròn, em hãy chỉ ra một vài cặp đường tròn cắt nhau và cặp đường tròn không giao nhau.

Cho hai điểm O và O’ cách nhau một khoảng 5 cm. Mỗi đường tròn sau đây có vị trí tương đối như thế nào đối với đường tròn (O; 3 cm) .
a) Đường tròn (O’; 3 cm)
b) Đường tròn (O’; 1 cm)
c) Đường tròn (O’; 8 cm)
Khi chuyển động, giả sử đầu mũi kim dài của một chiếc đồng hồ vạch nên một đường tròn, kí hiệu là (T1), trong khi đầu mũi kim ngắn vạch nên một đường tròn khác, kí hiệu là (T2).
a) Hai đường tròn (T1) và (T2) có vị trí tương đối như thế nào?
b) Giả sử bán kính của (T1) và (T2) lần lượt là R1 và R2. Người ta vẽ trên mặt đồng hồ một họa tiết hình tròn có tâm nằm cách điểm trục kim đồng hồ một khoảng bằng \(\frac{1}{2}{{\rm{R}}_1}\) và có bán kính bằng \(\frac{1}{2}{{\rm{R}}_2}\). Hãy cho biết vị trí tương đối của đường tròn (T3) đối với mỗi đường tròn (T1) và (T2). Vẽ ba đường tròn đó nếu R1 = 3 cm, R2 = 2 cm.

Cho đường tròn (O) đường kính AB, tiếp tuyến xx’ tại A và tiếp tuyến yy’ tại B của (O). Một tiếp tuyến thứ ba của (O) tại điểm P (khác A và B) cắt xx’ tại M và cắt yy’ tại N.
a) Chứng minh rằng MN = MA + NB.
b) Đường thẳng đi qua O và vuông góc với AB cắt NM tại Q. Chứng minh rằng Q là trung điểm của đoạn MN.
c) Chứng minh rằng AB tiếp xúc với đường tròn đường kính MN.
Cho hai đường tròn \(\left( {{\rm{A;}}\,{{\rm{R}}_{\rm{1}}}} \right){\rm{, }}\left( {{\rm{B;}}\,{{\rm{R}}_{\rm{2}}}} \right){\rm{,}}\) trong đó \({{\rm{R}}_{\rm{2}}} < \,{{\rm{R}}_{\rm{1}}}.\) Biết rằng hai đường tròn (A) và (B) cắt nhau (H.5.44).
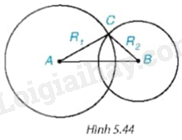
Khi đó:
A. \({\rm{AB}} < {{\rm{R}}_1} - \,{{\rm{R}}_{\rm{2}}}.\)
B. \({{\rm{R}}_1} - \,{{\rm{R}}_{\rm{2}}} < {\rm{AB}} < {{\rm{R}}_1} + \,{{\rm{R}}_{\rm{2}}}.\)
C. \({\rm{AB}} > {{\rm{R}}_1} + \,{{\rm{R}}_{\rm{2}}}.\)
D. \({\rm{AB}} = {{\rm{R}}_1} + \,{{\rm{R}}_{\rm{2}}}.\)
Cho điểm B nằm giữa hai điểm A và C, sao cho AB = 2 cm và BC = 1 cm. Vẽ các đường tròn (A; 1,5 cm), (B; 3 cm) và (C; 2 cm). Hãy xác định các cặp đường tròn:
a) Cắt nhau;
b) Không giao nhau;
c) Tiếp xúc với nhau.
Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Một đường thẳng d đi qua A cắt (O) tại E và cắt (O’) tại F (E và F) khác A. Biết điểm A nằm trong đoạn EF. Gọi I và K lần lượt là trung điểm của AE và AF (H.5.46).
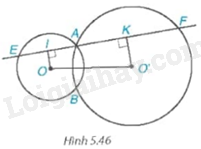
a) Chứng minh rằng tứ giác OO’KI là một hình thang vuông.
b) Chứng minh rằng \({\rm{IK}} = \frac{1}{2}{\rm{EF}}\).
c) Khi d ở vị trí nào (d vẫn qua A) thì OO’KI là một hình chữ nhật?
Tìm số điểm chung của hai đường tròn (O) và (O’) trong mỗi trường hợp sau:
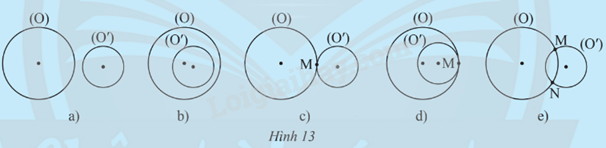
Cho hai đường tròn phân biệt (O;R) và (O’;R’) với R \( \ge \) R’.
Hãy so sánh OO’ với R + R’ và R – R’ trong mỗi trường hợp sau:
Trường hợp 1: (O;R) và (O’;R’) không có điểm chung (Hình 15).
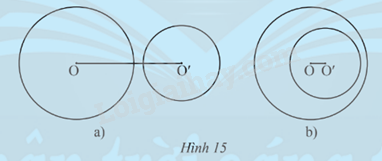
Trường hợp 2: (O;R) và (O’;R’) chỉ có 1 điểm chung (Hình 16).
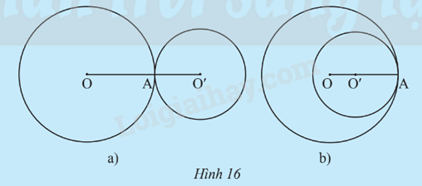
Trường hợp 3: (O;R) và (O’;R’) có đúng 2 điểm chung (Hình 17).
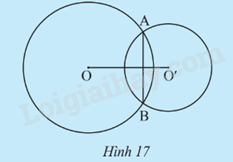
Xác định vị trí tương đối giữa hai đường tròn (I;R) và (J;R’) trong mỗi trường hợp sau:
a) IJ = 5; R = 3; R’ = 2
b) IJ = 4; R = 11; R’ = 7
c) IJ = 6; R = 9; R’ = 4
d) IJ = 10; R = 4; R’ = 1
Mô tả vị trí tương đối giữa mỗi cặp đường tròn trong hình chụp bộ cồng chiêng Tây Nguyên trong Hình 18.

Dùng compa đo bán kính và vẽ lại các hình trong Hình 19.
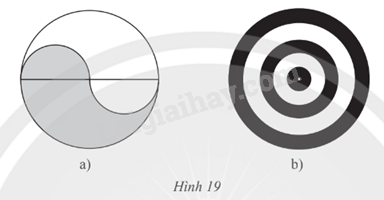
Xác định vị trí tương đối giữa hai đường tròn (O;R) và (O’;R’) trong mỗi trường hợp sau:
a) OO’ = 18; R = 10; R’ = 6
b) OO’ = 2; R = 9; R’ = 3
c) OO’ = 13; R = 8; R’ = 5
d) OO’ = 17; R = 15; R’ = 4
Cho hai đường tròn (O; 5 cm), (O’; 4 cm) với OO’ = 9 cm. Kết luận nào sau đây đúng về vị trí tương đối của hai đường tròn?
A. Hai đường tròn cắt nhau.
B. Hai đường tròn ở ngoài nhau.
C. Hai đường tròn tiếp xúc ngoài.
D. Hai đường tròn tiếp xúc trong.
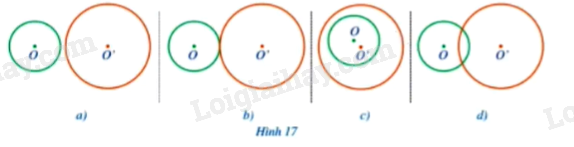
Xác định vị trí tương đối của hai đường tròn (O) và (O') trong mỗi hình \(17a,17b,17c,17d\):
Chiếc đồng hồ trang trí ở Hình 18 gợi nên vị trí tương đối của các đường tròn. Quan sát Hình 18 và chỉ ra một cặp đường tròn:

a) Cắt nhau;
b) Tiếp xúc ngoài;
c) Tiếp xúc trong;
d) Không giao nhau.
Cho hai đường tròn cùng tâm \(\left( {O;R} \right),\left( {O;r} \right)\) với \(R > r\). Các điểm \(A,B\) thuộc đường tròn \(\left( {O;R} \right)\), các điểm \(A',B'\) thuộc đường tròn \(\left( {O;r} \right)\) sao cho \(O,A,A'\) thẳng hàng; \(O,B,B'\) thẳng hàng và điểm \(O\) không thuộc đường thẳng \(AB\). Chứng minh:
a) \(\frac{{OA'}}{{OA}} = \frac{{OB'}}{{OB}}\).
b) \(AB//A'B'\).
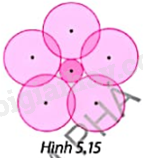
Trong Hình 5.15, mẫu trang trí hoa đào được tạo hình từ sáu đường tròn. Vị trí cánh hoa so với nhụy hoa và so với cánh hoa khác được mô tả thế nào?
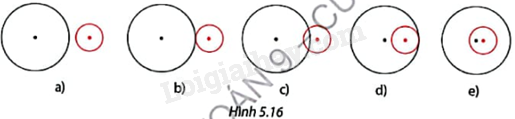
Hình 5.16 thể hiện vị trí tương đối khác nhau của hai đường tròn khi đường tròn nhỏ di chuyển từ ngoài vào phía trong đường tròn lớn. Nêu số điểm chung của hai đường tròn trong mỗi trường hợp.
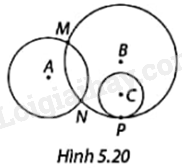
Chỉ ra các cặp đường tròn cắt nhau, tiếp xúc nhau và không giao nhau trong Hình 5.20.
Cho đường tròn bán kính \(R = 11cm\) và \(r = 7cm\). Xác định vị trí tương đối của hai đường tròn nếu khoảng cách giữa hai tâm bằng:
a) 2cm;
b) 4cm;
c) 21cm;
d) 18cm;
e) 15cm.
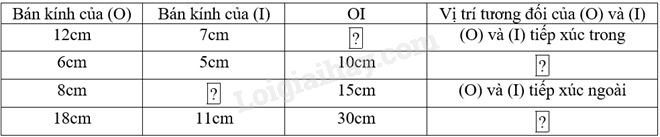
Thay các ô ? trong bảng dưới đây bằng một độ dài hoặc một khẳng định thích hợp:
Cho hai đường tròn tâm O và I cắt nhau tại M và N. Vẽ một đường thẳng qua M cắt (O) tại A và cắt (I) tại B, một đường thẳng qua N cắt (O) tại C và (I) tại D. Chứng minh rằng AC//BD.
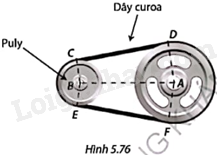
Trong Hình 5.76, hai puly có dạng hình tròn tâm A bán kính 12,5cm và tâm B bán kính 7cm được nối bằng dây curoa. Khoảng cách giữa tâm của hai puly là \(AB = 30cm\). Đoạn dây CD, EF tiếp xúc với cả hai puly. Tính:
a) Độ dài CD và số đo các góc của tứ giác ABCD;
b) Độ dài dây curoa.
Làm tròn độ dài đến hàng phần mười centimét, số đo góc đến phút.
Nối vị trí tương đối của hai đường tròn (cột A) với số tiếp tuyến chung có thể vẽ của hai đường tròn đó (cột B) để có đáp án đúng.
Hai đường tròn (O; 2cm) và (O’; 3cm) có vị trí tương đối như thế nào trong mỗi trường hợp sau:
a) \(OO' = 4cm\)?
b) \(OO' = 5cm\)?
c) \(OO' = 6cm\)?
Vẽ hình và chứng minh phần b của Ví dụ 2.
Ví dụ 2: Cho đường tròn (O) và dây AB không là đường kính của (O).
a) Gọi O' là một điểm tùy ý nằm giữa O và A. Đường thẳng đi qua O' và song song với OB cắt AB tại C. Hãy xác định vị trí tương đối của (O) và (O'; O'C).
b) Vị trí tương đối của (O) và (O'; O'C) sẽ như thế nào nếu O' thẳng hàng với O và A, nhưng nằm ngoài đoạn OA?
Cho hai điểm A và B sao cho \(AB = 7cm\) và đường tròn (B; 4cm). Khi đó:
A. Hai đường tròn (A; R) và (B) cắt nhau nếu \(R < 11cm\).
B. Hai đường tròn (A; R) và (B) cắt nhau nếu \(R > 3cm\).
C. Hai đường tròn (A; R) và (B) không giao nhau nếu \(R > 11cm\).
D. Hai đường tròn (A; R) và (B) không giao nhau nếu \(R \le 3cm\).







Danh sách bình luận