Tính độ dài cạnh x, y và số đo góc \(\alpha \) trong mỗi trường hợp ở Hình 4.23.
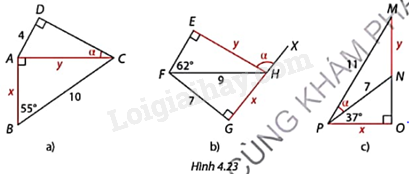
Hình a: \(\Delta \)ABC vuông tại A nên \(y = BC.\sin B;x = BC.\cos B\)
\(\Delta \)ADC vuông tại D nên \(\sin \alpha = \frac{{AD}}{{AC}}\) nên tính được \(\alpha \).
Hình b:
+ \(\Delta \)GFH vuông tại F nên \(F{G^2} + G{H^2} = F{H^2}\) nên tính được x
\(\sin GHF = \frac{{FG}}{{FH}} = \frac{7}{9}\) nên tính được góc FHG.
+ \(\Delta \)EFH vuông tại E nên \(y = FH.\sin EFH,\widehat {EHF} = {90^o} - \widehat {EFH}\). Do đó, \(\alpha = {180^o} - \widehat {EHF} - \widehat {FHG}\).
Hình c:
+ \(\Delta \)ONP vuông tại O nên \(x = PN.\cos NPO,NO = PN.\sin NPO\)
+ \(\Delta \)OMP vuông tại O nên \(\cos OPM = \frac{{OP}}{{PM}}\) nên tính được góc OPM, \(MO = PM.\sin MPO\)
Do đó, \(\alpha = \widehat {OPM} - \widehat {OPN},y = MN = MO - NO\)
Hình a:
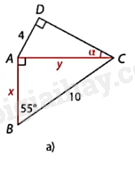
\(\Delta \)ABC vuông tại A nên
\(y = BC.\sin B = 10\sin {55^o} \approx 8,2;x = BC.\cos B = 10\cos {55^o} \approx 5,7\)
Tam giác ADC vuông tại D nên
\(\sin \alpha = \frac{{AD}}{{AC}} = \frac{4}{{8,2}} = \frac{{20}}{{41}}\) nên \(\alpha \approx {29^o}12'\).
Hình b:
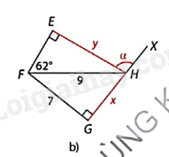
\(\Delta \)GFH vuông tại F nên \(F{G^2} + G{H^2} = F{H^2}\) (định lí Pythagore) nên \(x = GH = \sqrt {F{H^2} - F{G^2}} = \sqrt {{9^2} - {7^2}} = 4\sqrt 2 \approx 5,7\)
\(\sin GHF = \frac{{FG}}{{FH}} = \frac{7}{9}\) nên \(\widehat {FHG} \approx {51^o}3'\)
\(\Delta \)EFH vuông tại E nên
\(y = FH.\sin EFH = 9.\sin {62^o} \approx 7,9\), \(\widehat {EHF} = {90^o} - \widehat {EFH} = {90^o} - {62^o} = {28^o}\).
Do đó, \(\alpha = {180^o} - \widehat {EHF} - \widehat {FHG}\) \( \approx {180^o} - {28^o} - {29^o}11'\) \( \approx {122^o}49'\).
Hình c:
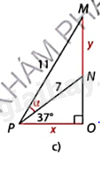
\(\Delta \)ONP vuông tại O nên \(x = PN.\cos NPO = 7.\cos {37^o} \approx 5,6\), \(NO = PN.\sin NPO = 7.\sin {37^o} \approx 4,2\).
\(\Delta \)OMP vuông tại O nên \(\cos OPM = \frac{{OP}}{{PM}} \approx \frac{{5,6}}{{11}}\) nên \(\widehat {OPM} \approx {59^o}24'\),
\(MO = PM.\sin MPO = 11.\sin {59^o}24' \approx 9,5\)
Do đó, \(\alpha = \widehat {OPM} - \widehat {OPN} \approx {22^o}24',y = MN = MO - NO \approx 5,3\)
Các bài tập cùng chuyên đề
Cho tam giác $MNP$ vuông tại $N$. Hệ thức nào sau đây là đúng?
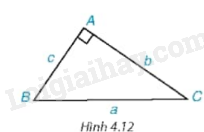
Cho tam giác ABC vuông tại A, cạnh huyền a và các cạnh góc vuông b, c (H.4.12).
a) Viết các tỉ số lượng giác sin, cosin của góc B và góc C theo độ dài các cạnh của tam giác ABC.
b) Tính mỗi cạnh góc vuông b và c theo cạnh huyền a và các tỉ số lượng giác trên góc B và góc C.
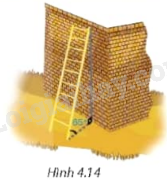
a) Một chiếc thang dài 3m. Cần đặt chân thang cách chân tường một khoảng bằng bao nhiêu mét (làm tròn đến số thập phân thứ hai) để nó tạo được với mặt đất một góc “an toàn” \({65^0}\) (tức là đảm bảo thang chắc chắn khi sử dụng) (H.4.14) ?
b) Một khúc sông rộng khoảng 250 m. Một con đò chèo qua khúc sông bị dòng nước đẩy xiên nên phải chèo khoảng 320 m mới sang được bờ bên kia. Hỏi dòng nước đã đẩy con đò đi lệch một góc \(\alpha \) bằng bao nhiêu độ (làm tròn đến phút) ? (H.4.15).
Tính góc nghiêng \(\alpha \) của thùng xe chở rác trong Hình 4.22 (làm tròn đến độ)
Cho tam giác ABC vuông tại A có độ dài cạnh huyền bằng 20cm. Tính độ dài các cạnh góc vuông trong mỗi trường hợp sau (kết quả làm tròn đến hàng phần trăm)
a) \(\widehat B = {36^o}\)
b) \(\widehat C = {41^o}\)
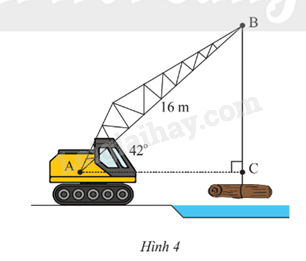
Một cần cẩu đang nâng một khối gỗ trên sông. Biết tay cần cẩu AB có chiều dài là 16m và nghiêng một góc \({42^o}\) so với phương nằm ngang (Hình 4). Tính chiều dài BC của đoạn dây cáp (kết quả làm tròn đến hàng phần mười).
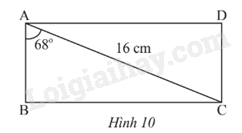
Tính các cạnh của hình chữ nhật ABCD. Biết AC = 16 cm và \(\widehat {BAC} = {68^o}\) (Hình 10).
Cho tam giác ABC có BC = 20 cm, \(\widehat {ABC} = {22^o},\widehat {ACB} = {30^o}\)
a) Tính khoảng cách từ điểm B đến đường thẳng AC.
b) Tính các cạnh và các góc còn lại của tam giác ABC.
c) Tính khoảng cách từ điểm A đến đường thẳng BC.
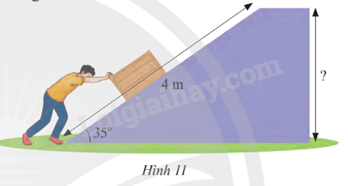
Một người đẩy một vật lên hết một con dốc nghiêng một góc 35o (Hình 11).
Tính độ cao của vật so sới mặt đất biết độ dài con dốc là 4 m.
Cho Hình 2.
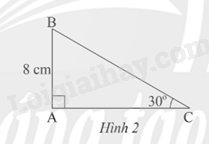
Độ dài cạnh BC là:
A. 4 cm
B. \(8\sqrt 3 \) cm
C. \(\frac{{8\sqrt 3 }}{3}\) cm
D. 16 cm
Một cái thang dài 3m đặt sát bờ tường, biết góc tạo bởi thang và bờ tường là 40o . Hỏi chân thang đặt ở vị trí cách tường bao nhiêu mét (kết quả làm tròn đến hàng phần mười)?
A. 1,9 m
B. 2,3 m
C. 1,8 m
D. 2,5 m
Một chiếc máy bay bay lên với tốc độ 450 km/h. Đường bay len tạo với phương nằm ngang một góc 30o . Hỏi sau 3 phút kể từ lúc cất cánh, máy bay cách mặt đất bao nhiêu kilomet theo phương thẳng đứng?
A. 10,5 km
B. 12,75 km
C. 12 km
D. 11,25 km
Hình 12b mô tả đường lên dốc ở Hình 12a, trong đó góc giữa \(BC\) và phương nằm ngang \(BA\) là \(\widehat {ABC} = 15^\circ \). Cạnh góc vuông \(AC\) và cạnh huyền \(BC\) (Hình 12b) có liên hệ với nhau như thế nào?
Cho tam giác \(ABC\) vuông tại \(A\) (Hình 13).
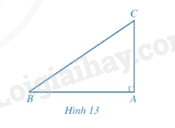
a) Biểu diễn \(\sin B,\cos C\) theo \(AC,BC\).
b) Viết công thức tính \(AC\) theo \(BC\) và \(\sin B\).
c) Viết công thức tính \(AC\) theo \(BC\) và \(\cos C\).
Tính độ cao \(AC\) trong Hình 12 khi \(BC = 20m\) (làm tròn kết quả đến hàng phần mười của mét)
Cho tam giác nhọn \(ABC\) có đường cao \(CK\). Biểu thị \(CK\) theo \(AC\) và \(\sin A\). Từ đó, chứng minh diện tích tam giác \(ABC\) bằng \(\frac{1}{2}.AB.AC.\sin A\).
Cho tam giác \(ABC\) vuông tại \(A\) có \(\widehat B = 30^\circ \). Chứng minh \(AC = \frac{1}{2}BC\).
Cho tam giác \(ABC\) vuông cân tại \(A\). Chứng minh \(AB = AC = \frac{{\sqrt 2 }}{2}BC\).
Cho hình thoi \(ABCD\) có \(AB = a,\widehat {BAD} = 2\alpha \left( {0^\circ < \alpha < 90^\circ } \right)\). Chứng minh:
a) \(BD = 2a.\sin \alpha \).
b) \(AC = 2a.\cos \alpha \).
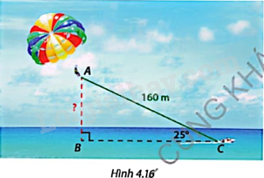
Ca nô dù bay là một trò chơi thể thao biển được ưa chuộng, trong đó người chơi được đeo dù và được ca nô kéo bay lên để thưởng ngoạn cảnh biển từ trên cao như Hình 4.17. Nếu biết độ dài AC của dây kéo và góc ACB tạo bởi dây và phương ngang, làm thế nào để tính được độ cao AB của người chơi so với mặt biển?
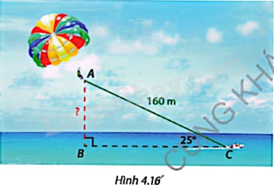
Quay lại bài toán ở phần Khởi động. Góc tạo bởi dây kéo dù bay và phương ngang là \(\widehat {ACB} = {25^o}\).
a) Tính độ cao AB của dù bay nếu dây kéo AC dài 160m.
b) Nếu muốn bay cao 75m thì dây kéo phải dài bao nhiêu mét?
Làm tròn kết quả đến hàng phần mười mét.
Bài toán khởi động: Ca nô dù bay là một trò chơi thể thao biển được ưa chuộng, trong đó người chơi được đeo dù và được ca nô kéo bay lên để thưởng ngoạn cảnh biển từ trên cao như Hình 4.17.
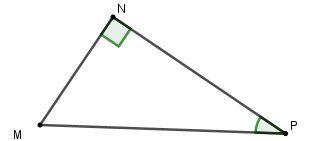
Cho tam giác \(MNP\) vuông tại \(N\). Hệ thức nào sau đây là đúng?
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 12\,cm,\widehat B = 40^\circ .\) Tính $AC;\widehat C$ . (làm tròn đến chữ số thập phân thứ hai)
Cho tam giác \(ABC\) có \(AB = 16,AC = 14\) và \(\widehat B = {60^0}\). Tính $BC$
Cho tam giác \(ABC\) có \(AB = 12,AC = 15\) và \(\widehat B = {60^0}\). Tính \(BC\)
Tính diện tích hình bình hành \(ABCD\) biết \(AD = 12cm;DC = 15cm;\angle ADC = {70^0}\).
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\), biết \(HB = 9;HC = 16\). Tính góc \(B\) và góc \(C.\)
Cho tam giác ABC vuông tại A có AB = 21cm, \(\widehat C = 47^\circ \). Tính độ dài đường phân giác BD của tam giác ABC (làm tròn kết quả đến hàng phần trăm của centimet).
Chứng minh diện tích tam giác đều cạnh a là \(\frac{{{a^2}\sqrt 3 }}{4}\).
Một cầu trượt trong công viên có độ dốc là 28o và có độ cao là 2,1 m. Độ dài của mặt cầu trượt (kết quả làm tròn đến hàng phần mười) là
A. 6,8 m
B. 4,5 m
C. 3,9 m
D. 3,3 m
