Tính chiều cao của một hình nó có đường sinh dài 20 cm và diện tích xung quanh bằng 240\(\pi \)cm2.
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rn\) (với r là bán kính đáy và n là đường sinh của hình nón).
Ta có:\({S_{xq}} = \pi rn\)
suy ra r = \(\frac{{{S_{xq}}}}{{\pi .n}} = \frac{{240\pi }}{{\pi .20}} = 12\)cm.
Từ đó, ta có chiều cao của hình nón là:
\(\sqrt {{{20}^2} - {{12}^2}} = 16\) cm (Theo định lý Pythagore).

Các bài tập cùng chuyên đề
Người ta coi diện tích hình quạt SAB (xem Thực hành 2) chính là diện tích xung quanh của hình nón được tạo thành. Cho hình nón có đường sinh \(l = 9cm\) và bán kính đáy \(r = 5cm\). Tính diện tích mặt xung quanh của hình nón.
Cho hình nón có bán kính đáy \(R = 2cm\), độ dài đường sinh \(l = 5cm\). Diện tích xung quanh của hình nón đã cho bằng
A. \(\frac{{10\pi }}{3}\;c{m^2}\).
B. \(\frac{{50\pi }}{3}\;c{m^2}\).
C. \(20\pi \;c{m^2}\).
D. \(10\pi \;c{m^2}\).
Bạn Khôi làm một chiếc mũ sinh nhật bằng bìa cứng có dạng hình nón với đường kính đáy bằng 20cm, độ dài đường sinh bằng 30cm. Tính diện tích giấy để làm chiếc mũ sinh nhật trên (lấy \(\pi \approx 3,14\) và coi mép dán không đáng kể).

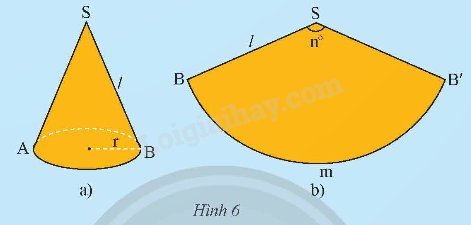
Cho một hình nón có bán kính r, có độ dài đường sinh l (Hình 6a). Cắt mặt xung quanh của hình nón theo một đường sinh của nó rồi trải phẳng ra, ta được hình quạt tròn (Hình 6b). Tính theo r và l:
a) Độ dài cung BB’;
b) Số đo cung BB’;
c) Diện tích của hình quạt tròn.
Tính diện tích xung quanh và diện tích toàn phần của hình nón có đường kính đáy d = 10 m và chiều cao h = 12 m (kết quả làm tròn đến hàng phần trăm).
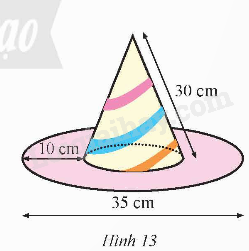
Một cái mũ chú hề có kích thước như Hình 13. Hãy tính tổng diện tích giấy làm nên chiếc mũ (không tính phần hao hụt, kết quả làm tròn đến hàng đơn vị).
Diện tích xung quanh của hình nón có chiều cao 12 cm và bán kính đáy 5 cm là
A. 130\(\pi \)cm2.
B. 60\(\pi \)cm2.
C. 65\(\pi \)cm2.
D. 90\(\pi \)cm2.
Người ta cần sơn mặt bên trong của một chao đèn có dạng hình nón (không tính đáy) với bán kính đáy là 20 cm, độ dài đường sinh là 30 cm (Hình 1c). Hỏi diện tích cần sơn là bao nhiêu?
Một chiếc nón lá có dạng hình nón với đường kính đáy khoảng 44 cm, chiều cao khoảng 20 cm. Hỏi diện tích xung quanh của chiếc nón đó bằng bao nhiêu centimét vuông (làm tròn kết quả đến hàng đơn vị)?

Phần mái lá của một ngôi nhà có dạng hình nón (không có đáy) với đường kính đáy khoảng 12 m và độ dài đường sinh khoảng 8,5 m (Hình 26). Chi phí để làm phần mái lá đó là 250 000 đồng/1 \(m^2\). Hỏi tổng chi phí để làm toàn bộ phần mái nhà đó là bao nhiêu đồng? (lấy \(\pi \approx 3,14\))

Cắt mặt xung quanh của một hình nón có đường sinh dài 6 cm, bán kính đáy 2 cm (Hình 9.22a) dọc theo đường sinh SA của nó rồi trải phẳng ra, ta được hình khai triển của hình nón đó (Hình 9.22b).
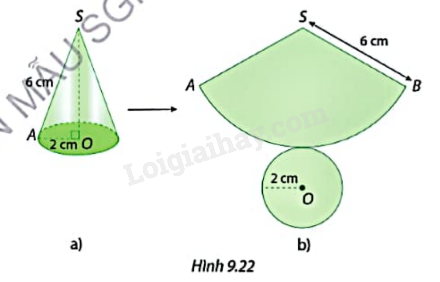
a) Tính chu vi đáy của hình nón, từ đó cho biết độ dài cung ứng với hình quạt tròn ở Hình 9.22b.
b) Tính diện tích của hình quạt tròn khai triển trong Hình 9.22b.
Nón lá phổ biến ở cả ba miền của nước ta nhưng nón lá Huế từ lâu đã trở thành nguồn cảm hứng cho thi ca. Nón Huế thường có màu trắng xanh, thanh tao, mỏng, nhẹ, mềm mại. Nón lá Huế có khung gồm 16 vòng cách đều nhau (khuôn nón còn được gọi là khung chằm) và được lợp bằng nhiều lớp lá của cây lá nón trồng ở huyện A Lưới và huyện Nam Đông, thuộc tỉnh Thừa Thiên Huế. Tính diện tích bề mặt ngoài (theo centimet vuông) của một chiếc nón lá có đường kính đáy 41 cm và chiều cao 18 cm (làm tròn kết quả đến hàng phần mười).
Cho hình nón có bán kính đáy R = 3 (cm) và đường sinh l = 5 (cm). Diện tích xung quanh của hình nón là:
-
A.
25π (cm2).
-
B.
12π (cm2).
-
C.
20π (cm2).
-
D.
15π (cm2).
Cái mũ của chú hề với các kích thước theo hình vẽ. Hãy tính tổng diện tích vải cần có để làm nên cái mũ (không kể riềm, mép, phần thừa).

-
A.
\(375\pi \left( {c{m^2}} \right)\).
-
B.
\(475\pi \left( {c{m^2}} \right)\).
-
C.
\(575\pi \left( {c{m^2}} \right)\).
-
D.
\(675\pi \left( {c{m^2}} \right)\).
Nón lá là một vật dụng dùng để che nắng, che mưa, làm quạt ... và là một biểu tượng đặc trưng của người phụ nữ Việt Nam. Nón có cấu tạo là hình nón tròn xoay có đến 16 cái vành tròn khung, vành nón to nhất có đường kính BC = 50 cm, bên ngoài đan các lớp lá (lá cọ, lá buông, rơm, tre hoặc lá cối, ...). Diện tích lớp lá đan bên ngoài chiếc nón là bao nhiêu? Biết chiều cao của nón là h = 30 cm.
-
A.
\(115\pi \sqrt {61} \left( {c{m^2}} \right)\).
-
B.
\(120\pi \sqrt {61} \left( {c{m^2}} \right)\).
-
C.
\(125\pi \sqrt {61} \left( {c{m^2}} \right)\).
-
D.
\(130\pi \sqrt {61} \left( {c{m^2}} \right)\).
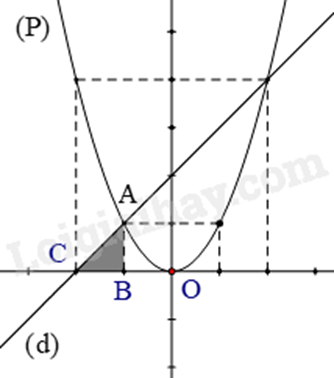
Cho Parabol (P): \(y = {x^2}\) và đường thẳng (d): \(y = x + 2\), có đồ thị như hình bên. Ta quay tam giác ABC một vòng quanh trục AB được hình nón. Diện tích xung quanh của hình nón là:
-
A.
\(\pi \sqrt 7 \).
-
B.
\(\pi \sqrt 5 \).
-
C.
\(\pi \sqrt 2 \).
-
D.
\(\pi \).
Nón Huế là một hình nón có đường kính đáy bằng \(40\) cm, độ dài đường sinh là \(30\) cm. Người ta lát mặt xung quanh hình nón bằng \(3\) lớp lá khô. Diện tích lá cần dùng để tạo nên một chiếc nón Huế như vậy bằng bao nhiêu \(c{m^2}\)? (lấy \(\pi \approx 3,14\))

Bạn Trang làm một chiếc mũ sinh nhật bằng giấy bìa màu, đường kính đáy bằng 16cm, độ dài đường sinh bằng 17cm. Tính diện tích bìa màu bạn Trang cần dùng để làm chiếc mũ sinh nhật đó (coi mép dán không đáng kể, làm tròn kết quả đến hàng đơn vị của \(c{m^2}\)).
Gọi l, h, R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của hình nón. Diện tích xung quanh của hình nón là
A. \({S_{xq}} = 2\pi Rl\).
B. \({S_{xq}} = \pi Rh\).
C. \({S_{xq}} = \pi Rl\).
D. \({S_{xq}} = \pi {R^2}h\).
Một chiếc nón lá có dạng một hình nón không có đáy, đường kính đáy bằng 80cm, chiều cao bằng 30cm. Tính diện tích mặt ngoài của chiếc nón (làm tròn kết quả đến hàng đơn vị của \(c{m^2}\)).
Để làm nón lá, người ta phải chuốt từng thanh tre mảnh, nhỏ, dẻo rồi uốn thành các vòng tròn có đường kính to nhỏ khác nhau tạo thành các vành nón. Vành lớn nhất của một chiếc nón lá có đường kính là 40 cm, khoảng cách từ đỉnh cao nhất đến một điểm trên vành này là 32 cm. Tính diện tích xung quanh của chiếc nón lá đó (kết quả làm tròn đến hàng đơn vị của xăngtimet vuông).

Cho một hình nón có thể tích là \(16\pi \) cm3 và bán kính đáy là 4 cm. Diện tích xung quanh của hình nón đó là
A. \(40\pi \) cm2
B. \(60\pi \) cm2
C. \(80\pi \) cm2
D. \(20\pi \) cm2
Một hình nón có chiều cao là 8 cm và đường kính đường tròn đáy bằng 12 cm. Tính diện tích xung quanh của hình nón đó.
Cho hình nón (N) có đường kính đường tròn đáy bằng 4a, đường sinh bằng 5a. Tính diện tích xung quanh của hình nón (N).
Khi quay tam giác OHA vuông cân ở H một vòng xung quanh đường thẳng cố định OH, ta được một hình nón như ở Hình 14. Hỏi diện tích xung quanh của hình nón đó là bao nhiêu centimét vuông (làm tròn kết quả đến hàng đơn vị)? Biết diện tích tam giác OHA là 4 cm2.
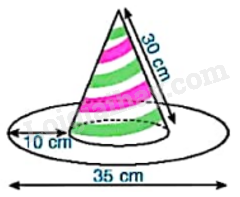
Chiếc mũ của chú hề với các kích thước như hình bên. Hãy tính tổng diện tích vải cần để làm nên chiếc mũ (coi mép khâu không đáng kể và làm tròn kết quả đến hàng phần mười của \(c{m^2}\)).
Cho hình nón có bán kính đáy \(r = 2cm\), độ dài đường sinh \(l = 5cm\). Diện tích xung quanh của hình nón đã cho bằng:
A. \(\frac{{10\pi }}{3}\;c{m^2}\).
B. \(\frac{{50\pi }}{3}\;c{m^2}\).
C. \(20\pi \;c{m^2}\).
D. \(10\pi \;c{m^2}\).
Nhà hát Cao Văn Lầu và Trung tâm triển lãm Văn hóa Nghệ thuật tỉnh Bạc Liêu có hình dáng ba chiếc nón lá lớn nhất Việt Nam. Tính diện tích mái nhà hình nón có đường kính bằng 45m và chiều cao bằng 24m (làm tròn kết quả đến hàng đơn vị của \({m^2}\)).

Bạn Khôi làm một chiếc mũ sinh nhật bằng bìa cứng có dạng hình nón với đường kính đáy bằng 20cm, độ dài đường sinh bằng 30cm. Tính diện tích giấy để làm chiếc mũ sinh nhật trên (lấy \(\pi \approx 3,14\) và coi mép dán không đáng kể).








Danh sách bình luận