Khi phân tích các số \(2150;1490;2340\) ra thừa số nguyên tố thì số nào có chứa tất cả các thừa số nguyên tố \(2;3\) và \(5?\)
-
A.
$2340$
-
B.
$2150$
-
C.
$1490$
-
D.
Cả ba số trên.
Sử dụng cách phân tích một số ra thừa số nguyên tố theo hàng dọc. Từ đó xét xem số nào được phân tích ra thừa số nguyên tố mà chứa cả các thừa số nguyên tố \(2;3\) và \(5.\)
+) Phân tích số \(2150\) thành thừa số nguyên tố
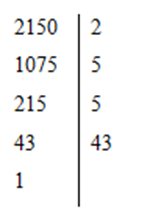
Suy ra \(2150 = {2.5^2}.43\)
+) Phân tích số \(1490\) thành thừa số nguyên tố
Suy ra \(1490 = 2.5.149\)
+) Phân tích số \(2340\) thành thừa số nguyên tố
Suy ra \(2340 = {2^2}{.3^2}.5.13\)
Vậy có số \(2340\) thỏa mãn yêu cầu đề bài.
Đáp án : A
Các bài tập cùng chuyên đề
Phân tích số \(a\) ra thừa số nguyên tố \(a = p_1^{{m_1}}.p_2^{{m_2}}...p_k^{{m_k}}\), khẳng định nào sau đây là đúng:
Phân tích số $18$ thành thừa số nguyên tố:
Cho số $a = {2^2}.7$, hãy viết tập hợp tất cả các ước của $a$:
Cho ${a^2}.b.7 = 140$ với \(a,b\) là các số nguyên tố, vậy \(a\) có giá trị là bao nhiêu:
Cho số ${\rm{150 = 2}}{\rm{.3}}{\rm{.}}{{\rm{5}}^2}$, số lượng ước của $150$ là bao nhiêu:
Tích của hai số tự nhiên bằng \(105.\) Có bao nhiêu cặp số thỏa mãn?
Số $360$ khi phân tích được thành thừa số nguyên tố, hỏi tích đó có bao nhiêu thừa số là số nguyên tố?
Số các ước của số $192$ là
Cho phép tính \(\overline {ab} .\,c\, = 424.\) Khi đó \(c\) bằng bao nhiêu?
Một hình vuông có diện tích là \(1936\,{m^2}.\) Tính cạnh của hình vuông đó.
Số 40 được phân tích thành các thừa số nguyên tố là:
Biết \(400 = {2^4}{.5^2}\). Hãy viết 800 thành tích các thừa số nguyên tố
225 chia hết cho tất cả bao nhiêu số nguyên tố?
Cho cách phân tích 24 thành tích các thừa số nguyên tố như sau
$a,b,c$ lần lượt là
Số nào trong các số sau là ước nguyên tố của 52?
Khi phân tích 104 thành tích các thừa số nguyên tố thì số mũ của thừa số 2 là
