Bác An muốn sơn mặt xung quanh của một cây cột có dạng hình trụ với đường kính đáy là 30cm và chiều cao là 350cm. Chi phí để sơn cây cột đó là 40.000 đồng/m2. Hỏi chi phí bác An cần bỏ ra để sơn mặt xung quanh cây cột đó là bao nhiêu đồng (làm tròn kết quả đến hàng nghìn).
Bước 1: Tính diện tích xung quanh của hình trụ.
Bước 2: Số tiền bỏ ra bằng \({S_{xq}}.40000\).
Bán kính đáy là:
\(30:2 = 15(cm).\)
Diện tích xung quanh của cây cột hình trụ là:
\({S_{xq}} = 2\pi rh = 2\pi .15.350 = 10500\pi \left( {c{m^2}} \right) = 1,05\pi \left( {{m^2}} \right).\)
Chi phí bác An cần bỏ ra là:
\(1,05\pi.40000 = 42000\pi \approx 132000\) đồng.

Các bài tập cùng chuyên đề
Người ta coi diện tích hình chữ nhật ABCD chính là diện tích xung quanh của hình trụ được tạo thành (xem Thực hành 1). Cho hình trụ có chiều cao \(h = 9cm\) và bán kính đáy \(R = 5cm\). Tính diện tích mặt xung quanh của hình trụ.
Một nhà máy dự định sản xuất thùng phuy đựng dầu nhớt dạng hình trụ có đường kính đáy 0,6 m và chiều cao 0,9 m (Hình 7). Bỏ qua diện tích các mép thùng, hãy tính diện tích thép cần để sản xuất 100 thùng phuy như vậy (kết quả làm tròn đến hàng phần trăm).

Phần bên trong một chiếc thùng có dạng hình trụ với bán kính đáy 0,6 m , chiều cao 0,8 m. Người ta muốn sơn mặt bên trong hình trụ (bao gồm mặt đáy). Hỏi diện tích cần sơn là bao nhiêu (kết quả làm tròn đến hàng phần trăm).
Diện tích xung quanh của hình trụ có bán kính đáy 4 cm và chiều cao 8 cm là
A. 32\(\pi \)cm2.
B. 48\(\pi \)cm2.
C. 64\(\pi \)cm2.
D. 128\(\pi \)cm2.
Thực hiện các hoạt động sau:
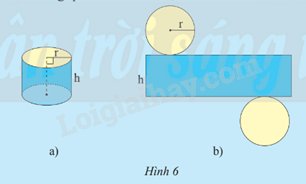
a) Chuẩn bị một hình trụ bằng giấy có bán kính đáy r và chiều cao h (Hình 6a).

b) Từ hình trụ đó, cắt rời hai đáy và cắt dọc theo đường sinh AB rồi trải phẳng ra, ta được hình khai triển mặt xung quanh của hình trụ là một hình chữ nhật (Hình 6b);
c) Hãy cho biết độ dài các cạnh của hình chữ nhật ở hình 6b và tính diện tích hình chữ nhật đó theo r và h.
Một doanh nghiệp sản xuất vỏ hộp bằng tôn có dạng hình trụ với hai đáy (Hình 13). Hình trụ đó có đường kính đáy khoảng 57 cm và chiều cao khoảng 89 cm. Chi phí để sản xuất vỏ hộp đó là 100 000 đồng/m2. Hỏi số tiền mà doanh nghiệp cần chi để sản suất 1 000 vỏ hộp đó là bao nhiêu đồng (Lấy \(\pi \approx 3,14\), làm tròn kết quả đến hàng nghìn).

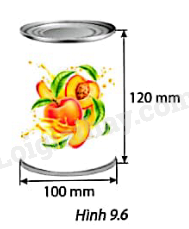
Một hộp hình trụ làm bằng thiếc có bán kính 5 cm, chiều cao 8 cm (Hình 9.4a). Nếu cắt rời hai đáy và cắt dọc theo đường sinh AB của hộp, rồi trải phẳng ra, ta được hình khai triển của hình trụ (Hình 9.4b).
a) Tính chu vi mỗi đáy của hình trụ.
b) Tính diện tích miếng thiếc hình chữ nhật để làm thành mặt xung quanh của hộp (diện tích các mối nối không đáng kể).
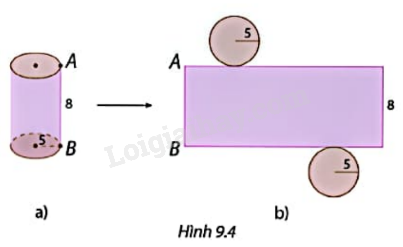
Tính diện tích xung quanh của hình trụ có hình khai triển như Hình 9.5.
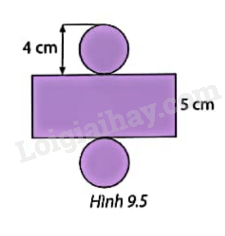
Diện tích giấy tối thiểu để quấn quanh một hộp đào ngâm có dạng hình trụ (Hình 9.6) là bao nhiêu centimet vuông (làm tròn kết quả đến hàng phần trăm), biết rằng người ta chỉ quấn một lớp giấy quanh hộp đào?
Tính diện tích xung quanh của hình trụ tạo thành khi quay hình chữ nhật ABCD có BC = 3 cm, CD = 4 cm quanh cạnh AB.
A. 12\(\pi \)cm2
B. 21\(\pi \)cm2
C. 24\(\pi \)cm2
D. 42\(\pi \)cm2
Cho hình trụ \(\left( T \right)\) có chiều cao \(h\), độ dài đường sinh \(l\), bán kính đáy \(r\). Ký hiệu \({S_{xq}}\) là diện tích xung quanh của \(\left( T \right)\). Công thức nào sau đây là đúng?
-
A.
\({S_{xq}} = 2\pi rl\).
-
B.
\({S_{xq}} = \pi rh\).
-
C.
\({S_{xq}} = 2\pi {r^2}h\).
-
D.
\({S_{xq}} = \pi rl\).
Cho hình trụ có bán kính đáy \(R = 3\,(cm)\) và chiều cao \(h = 6\,(cm)\). Diện tích xung quanh của hình trụ là:
-
A.
\(40\pi \).
-
B.
\(36\pi \).
-
C.
\(18\pi \).
-
D.
\(24\pi \).
Một cái trục lăn sơn nước có dạng một hình trụ. Đường kính của đường tròn đáy là 6cm, chiều dài lăn là 25cm (hình vẽ bên dưới). Sau khi lăn trọn 10 vòng thì trục lăn tạo nên bức tường phẳng một diện tích là bao nhiêu?

-
A.
\(1200\pi \,\left( {{c}{{m}^2}} \right)\).
-
B.
\(1500\pi \,\left( {{c}{{m}^2}} \right)\).
-
C.
\(150\pi \,\left( {{c}{{m}^2}} \right)\).
-
D.
\(1500\,\left( {{c}{{m}^2}} \right)\).
Mặt tiền của một ngôi biệt thự có \(8\)cây cột hình trụ tròn, tất cả đều có chiều cao \(4,2m\). Trong số các cây cột đó, có \(2\)cây cột trước đại sảnh đường kính bằng \(40cm\), \(6\)cây cột còn lại phân bố đều hai bên đại sảnh và chúng đều có đường kính bằng \(26cm\). Chủ nhà thuê một nhóm công nhân để sơn các cây cột bằng một loại sơn giả đá, biết giá thuê là \(400\,000/1{m^2}\)(gồm tiền sơn và tiền công thợ). Hỏi người chủ phải chi trả bao nhiêu tiền để sơn hết các cây cột nhà đó? (Lấy \(\pi \approx 3,14\)).
-
A.
\(12\,451\,472\) đồng.
-
B.
\(12\,450\,472\) đồng.
-
C.
\(12\,459\,472\) đồng.
-
D.
\(12\,449\,472\) đồng.
Người ta thiết kế một công trình kiến trúc như hình bên. Mái nhà là 3 hình nón có kích thước giống nhau. Tính số tiền sơn mặt trên của mái nhà, biết giá 1 (m2) = 200.000 vnđ, chiều cao bằng chiều rộng của hình nón. Chiều cao của mái nhà là giá trị nhỏ nhất của biểu thức: \(h = \frac{1}{{{a^{\rm{2}}} + 4{b^{\rm{2}}}}} + \frac{1}{{{b^{\rm{2}}}{\rm{ + 4}}{{\rm{a}}^{\rm{2}}}}} + \frac{4}{{{\rm{10ab}}}}\) thỏa mãn điều kiện hai số dương a, b; a + b = 1. (đơn vị là m) (lấy \(\pi \approx 3,14\), diện tích làm tròn đến chữ số thập phân thứ hai)

-
A.
27 284 000 (vnđ).
-
B.
28 284 000 (vnđ).
-
C.
29 284 000 (vnđ).
-
D.
30 284 000 (vnđ).
Hình khai triển của một hình trụ có bán kính đáy r, chiều cao h (Hình 6a) gồm hai hình tròn và một hình chữ nhật (Hình 6b). Diện tích của hình chữ nhật trong Hình 6b được gọi là diện tích xung quanh của hình trụ
Hãy tính diện tích xung quanh của hình trụ theo r và h.
Một trục lăn sơn có dạng hình trụ, đường kính của đường tròn đáy bằng 5cm, chiều dài bằng 23cm (H.10.2). Sau khi lăn trọn vẹn liên tục 15 vòng thì diện tích phần sơn được trên mặt tường phẳng là bao nhiêu?

Gọi h, R lần lượt là độ dài của chiều cao và bán kính đáy của hình trụ. Diện tích xung quanh của hình trụ là
A. \({S_{xq}} = 2\pi Rh\).
B. \({S_{xq}} = \pi Rh\).
C. \({S_{xq}} = \pi Rl\).
D. \({S_{xq}} = \pi {R^2}h\).
Một đoạn ống bằng thép dạng hình trụ có chiều cao 12 cm, bán kính đáy bên trong 2,1 cm, bán kính đáy bên ngoài 2,5 cm. Người ta muốn sơn toàn bộ mặt bên trong và mặt bên ngoài của đoạn ống này. Tính diện tích cần sơn (kết quả làm tròn đến hàng đơn vị của xăngtimet vuông).
Diện tích xung quanh của hình trụ có bán kính đáy 5 cm, chiều cao 10 cm là
A. 100\(\pi \) cm2
B. 200\(\pi \) cm2
C. 300\(\pi \) cm2
D. 400\(\pi \) cm2
Bác Long đã chi tiền để làm một cái bể hình trụ có bán kính đường tròn đáy là 0,8 m và có thể tích là 1,12π m3. Đáy bể làm bằng bê tông giá 100 000 đồng/m2. Phần thân làm bằng tôn inox giá 15 000 đồng/m2. Phần nắp làm bằng nhôm giá 12 000 đồng/m2. Hỏi số tiền bác Long đã chi để làm được cái bể đó là bao nhiêu đồng (làm tròn kết quả đến hàng nghìn)?
Một hình trụ có bán kính đáy bằng 3cm, chiều cao 6cm. Diện tích xung quanh của hình trụ là
A. \(36\pi \;c{m^2}\).
B. \(9\pi \;c{m^2}\).
C. \(12\pi \;c{m^2}\).
D. \(54\pi \;c{m^2}\).
Cho hình chữ nhật có chiều dài 3cm, chiều rộng 2cm. Quay hình chữ nhật đó một vòng quanh chiều dài của nó ta được một hình trụ có diện tích xung quanh bằng
-
A.
\(6\pi \)\(\left( {c{m^2}} \right)\).
-
B.
\(8\pi \)\(\left( {c{m^2}} \right)\).
-
C.
\(12\pi \)\(\left( {c{m^2}} \right)\).
-
D.
\(18\pi \)\(\left( {c{m^2}} \right)\).
Bạn Toán đi mua giúp bố cây lăn sơn ở cửa hàng nhà bác Học. Một cây lăn sơn tường có dạng một khối trụ với bán kính đáy là 5cm và chiều cao là 23 cm (hình vẽ bên). Nhà sản xuất cho biết sau khi lăn 1000 vòng thì cây sơn tường có thể bị hỏng. Hỏi bạn Toán cần mua ít nhất mấy cây lăn sơn tường, biết diện tích tường mà bố bạn Toán cần sơn là \(100{m^2}\). (Cho \(\pi \approx 3,14\))
Một cái mũ bằng vải của nhà ảo thuật với các kích thước như hình vẽ dưới đây. Hãy tính tổng diện tích vải cần có để làm nên cái mũ đó (không kể viền, mép, phần thừa).
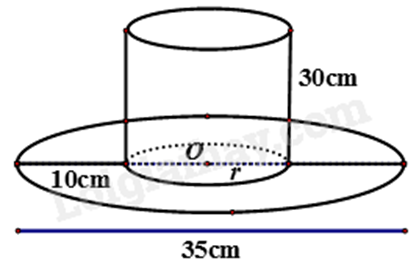
-
A.
\(750,25\pi \left( {c{m^2}} \right)\).
-
B.
\(700\pi \left( {c{m^2}} \right)\).
-
C.
\(756,25\pi \left( {c{m^2}} \right)\).
-
D.
\(754,25\pi \left( {c{m^2}} \right)\).
Một xe lu san đường (loại 1 trống lu) có đường kính trống lu là 0,96m và chiều dài trống lu là 169cm. Người ta sử dụng loại xe lu này để làm phẳng 1 sân bóng đá hình chữ nhật có kích thước 120m x 90m. Cho rằng sân bóng cần được lăn 5 lần thì đạt tiêu chuẩn và mỗi trống lu chỉ lăn được tối đa với công suất 10 000 vòng/tuần. Cần sử dụng ít nhất bao nhiêu xe lu để có thể hoàn thành công việc trong 1 tuần. (biết rằng mỗi xe đều lăn hết công suất cho phép và các xe lu chỉ lăn trên phần sân riêng biệt)







Danh sách bình luận