Cho điểm O cố định.
a) Xét điểm M tùy ý (khác O) và đường tròn (O;OM). Hãy tìm điểm M’ thuộc đường tròn (O; OM) sao cho chiều quay từ tia OM đến tia OM’ cùng chiều quay của kim đồng hồ và cung MnM’ có số đo \(120^\circ .\)
b) Xét điểm N tùy ý (khác O) và đường tròn (O;ON). Hãy tìm điểm N’ thuộc đường tròn (O; ON) sao cho chiều quay từ tia ON đến tia ON’ ngược chiều quay của kim đồng hồ và cung NpN’ có số đo \(300^\circ .\)
Thực hiện vẽ theo yêu cầu
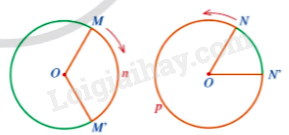
a)
- Vẽ đường (O; OM)
- Lấy điểm \( M' \in (O; OM)\) sao cho chiều quay từ tia OM đến tia OM' cùng chiều quay kim đồng hồ.
Xét đường (O; OM) có:
\( \widehat{MOM'} =\) số đo cung MM' \(= 120^\circ \)
b)
- Vẽ đường (O; ON)
- Lấy điểm \( N' \in (O; ON)\) sao cho chiều quay từ tia ON đến tia ON' ngược chiều quay kim đồng hồ.
Xét đường (O; ON) có:
\( \widehat{NON'} =\) số đo cung NN' \(= 360^\circ -\) số đo cung NpN' \)
\( = 360^\circ - 300^\circ = 60^\circ \)

Các bài tập cùng chuyên đề
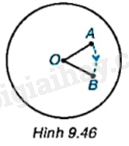
Để bày bàn ăn cho nhiều người, các nhà hàng thường sử dụng bàn xoay có hình tròn và quay được quanh tâm của hình tròn. Đặt một chiếc cốc nhỏ ở vị trí điểm A trên bàn xoay hình tròn với tâm O sao cho điểm A khác điểm O. Khi quay bàn xoay thuận chiều kim đồng hồ (H.9.46) thì chiếc cốc di chuyển đến một vị trí mới là điểm B.
Em hãy so sánh khoảng cách từ hai điểm A và B đến điểm O. Hai điểm A, B có cùng nằm trên một đường tròn tâm O hay không?
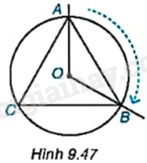
Trên bàn xoay tâm O, vẽ tam giác đều ABC nội tiếp một đường tròn (O) và hai tia OA, OB (H.9.47). Khi quay bàn xoay thuận chiều kim đồng hồ để tia OA di chuyển trùng với tia OB (ở vị trí ban đầu), điểm A có di chuyển đến điểm B không và sẽ di chuyển trên cung tròn nào của đường tròn (O)? Khi đó, điểm C sẽ di chuyển đến vị trí của điểm nào?
a) Phép quay ngược chiều \({180^o}\) tâm O biến điểm A thành điểm A’. Hỏi điểm A’ có đối xứng với điểm A qua O hay không?
b) Nếu phép quay thuận chiều \({\alpha ^o}\) tâm O biến điểm A thành điểm B thì phép quay ngược chiều \({\alpha ^o}\) tâm O biến điểm B thành điểm A hay không?
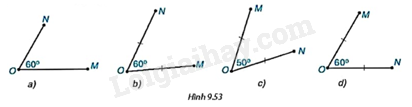
Trong các hình dưới đây (H.9.53), hình nào vẽ hai điểm M và N thỏa mãn phép quay thuận chiều \({60^o}\) tâm O biến điểm M thành điểm N?
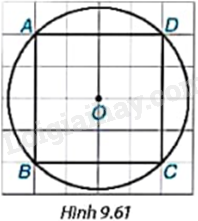
a) Phép quay thuận chiều \({45^o}\) tâm O biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D’ (H.9.61). Hãy vẽ tứ giác A’B’C’D’.
b) Phép quay trong câu a biến các điểm A’, B’, C’, D’ thành những điểm nào?
Vẽ hình vuông ABCD tâm O (Hình 5a). Cắt một tấm bìa hình vuông (gọi là H) cùng độ dài cạnh với hình vuông ABCD (Hình 5b). Đặt hình vuông H trùng khít lên hình vuông ABCD sao cho tại đỉnh M của H trùng với điểm A, rồi dùng đinh ghim cố định tâm của H tại tâm O của hình vuông ABCD (Hình 5c). Quay hình vuông H quanh điểm O ngược chiều kim đồng hồ cho đến khi đỉnh M của H trùng lại với đỉnh A (Hình 5d).
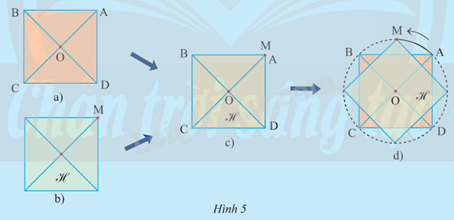
a) Khi điểm M trùng với B thì M vạch lên một cung tròn có số đo bằng bao nhiêu?
b) Trong quá trình trên, hình vuông H trùng khít với hình vuông ABCD bao nhiêu lần (không tính vị trí ban đầu trước khi quay)? Ứng với mỗi lần đó, điểm M vạch nên cung có số đo bao nhiêu?
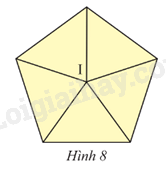
Tìm phép quay biến hình ngũ giác đều tâm I thành chính nó (Hình 8).
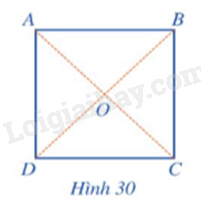
Cho hình vuông ABCD tâm O, chỉ ra phép quay thuận chiều tâm O sao cho phép quay đó biến mỗi điểm A, B, C, D thành điểm đối xứng với nó qua tâm O.
Cho hình vuông ABCD tâm O (Hình 30). Phép quay thuận chiều tâm O biến điểm A thành điểm D thì các điểm B, C, D tương ứng biến thành các điểm nào?
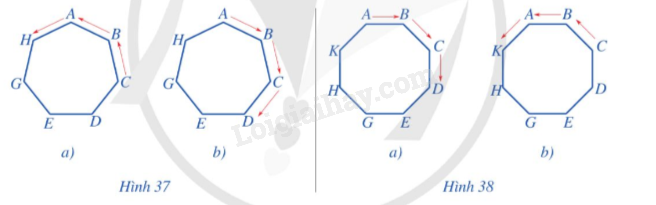
a) Ở Hình 37a, ta thực hiện phép quay giữ nguyên hình đa giác đều có 7 cạnh ABCDEGH và biến các điểm A, B, C, D, E, G, H lần lượt thành các điểm H, A, B, C, D, E, G. Phép quay đó là phép quay nào?
b) Ở Hình 37b, ta thực hiện phép quay giữ nguyên hình đa giác đều có 7 cạnh ABCDEGH và biến các điểm A, B, C, D, E, G, H lần lượt thành các điểm B, C, D, E, G, H, A. Phép quay đó là phép quay nào?
c) Ở Hình 38a, ta thực hiện phép quay giữ nguyên hình đa giác đều có 8 cạnh ABCDEGHK và biến các điểm A, B, C, D, E, G, H, K lần lượt thành các điểm B, C, D, E, G, H, K, A. Phép quay đó là phép quay nào?
d) Ở Hình 38b, ta thực hiện phép quay giữ nguyên hình đa giác đều có 8 cạnh ABCDEGHK và biến các điểm A, B, C, D, E, G, H, K lần lượt thành các điểm K, A, B, C, D, E, G, H. Phép quay đó là phép quay nào?
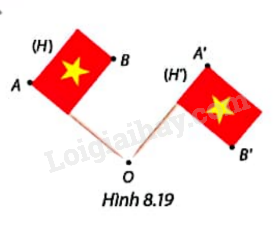
Trong Hình 8.19, Lá cờ (H) được quay quanh điểm O theo chiều kim đồng hồ đến vị trí mới (H’).
a) So sánh độ dài OA và OA’, OB và OB’.
b) So sánh số đo \(\widehat {AOA'}\) và \(\widehat {BOB'}\).
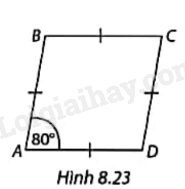
Cho hình thoi ABCD có \(\widehat A = {80^o}\) như Hình 8.23.
a) Tìm ảnh của điểm D qua phép quay ngược chiều \({80^o}\) tâm A.
b) Phép quay thuận chiều \({100^o}\) tâm B biến điểm C thành điểm nào?
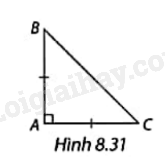
Cho tam giác ABC vuông cân tại A như Hình 8.31. Tìm ảnh của cạnh AB qua phép quay thuận chiều 90o tâm A.
Từ 3 giờ chiều đến 3 giờ 20 phút chiều, kim phút của đồng hồ thực hiện một phép quay thuận chiều \({\alpha ^o}\) tâm O. Tìm \(\alpha .\)

Cho tam giác ABC vuông cân tại A có D là trung điểm của cạnh BC (Hình 8.42).
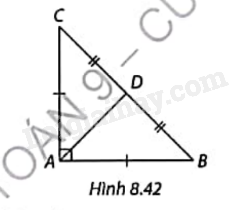
Khẳng định nào sau đây sai?
A. Phép quay thuận chiều 90o tâm A biến điểm C thành điểm B.
B. Phép quay ngược chiều 90o tâm D biến điểm C thành điểm A.
C. Phép quay ngược chiều 90o tâm D biến điểm A thành điểm B.
D. Phép quay thuận chiều 45o tâm A biến điểm B thành điểm D.
Cho hình vuông \(ABCD\)nội tiếp đường tròn \(\left( O \right)\) như hình. Phép quay thuận chiều \({90^o}\) tâm \(O\) biến các điểm \(A,B,C,D\) lần lượt thành các điểm:
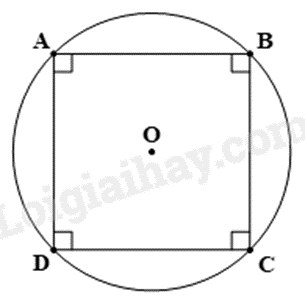
-
A.
\(B,C,D,A\).
-
B.
\(C,D,A,B\).
-
C.
\(D,A,B,C\).
-
D.
\(A,B,C,D\).
Cho lục giác đều \({{ABCDEF}}\) nội tiếp đường tròn \({{(O)}}\). Hãy tìm một phép quay thuận chiều biến điểm \({{A}}\) thành điểm \({{C}}\).
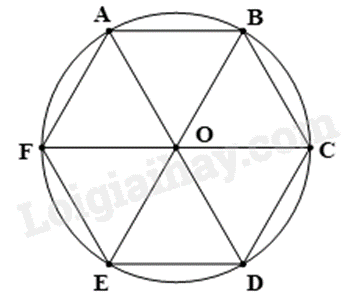
-
A.
Phép quay \(30^\circ \).
-
B.
Phép quay \(60^\circ \).
-
C.
Phép quay \(90^\circ \).
-
D.
Phép quay \(120^\circ \).
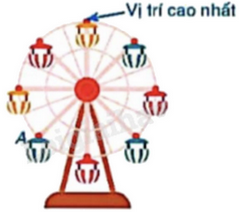
Cho mô hình vòng quay mặt trời gồm 8 cabin như hình vẽ. Để cabin A di chuyển đến vị trí cao nhất thì vòng quay phải quay
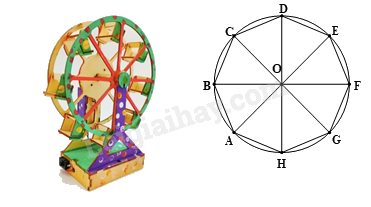
-
A.
thuận chiều kim đồng hồ quanh tâm O một góc \({60^o}\).
-
B.
ngược chiều kim đồng hồ quanh tâm O một góc \({60^o}\).
-
C.
thuận chiều kim đồng hồ quanh tâm O một góc \({135^o}\).
-
D.
ngược chiều kim đồng hồ quanh tâm O một góc \({135^o}\).
Trên mặt phẳng toạ độ Oxy, cho hình vuông ABCD với \(A\left( {1;{{ }}1} \right),{{ }}B\left( { - 1;{{ }}1} \right),{{ }}C\left( { - 1; - 1} \right),{{ }}D\left( {1; - 1} \right)\). Phép quay ngược chiều \(45^\circ \) tâm O biến các điểm A, B, C, D lần lượt thành các điểm A', B', C', D'. Tính diện tích tứ giác A'B'C'D'.
-
A.
6 đơn vị diện tích
-
B.
8 đơn vị diện tích
-
C.
4 đơn vị diện tích
-
D.
5,5 đơn vị diện tích
Cho hình đa giác đều có 9 cạnh ABCDEFGHI với tâm O.
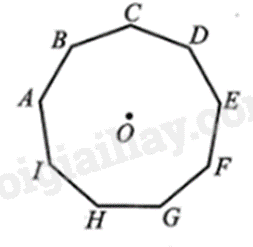
Phép quay ngược chiều \(120^\circ \) tâm O biến A thành điểm nào?
Khi quan sát la bàn (Hình a), bác An thấy con tàu mà bác điều khiển đang đi thẳng và di chuyển về hướng Bắc. Hỏi bác phải thực hiện phép quay nào trên bánh lái (Hình b) để con tàu rẽ sang hướng Đông?
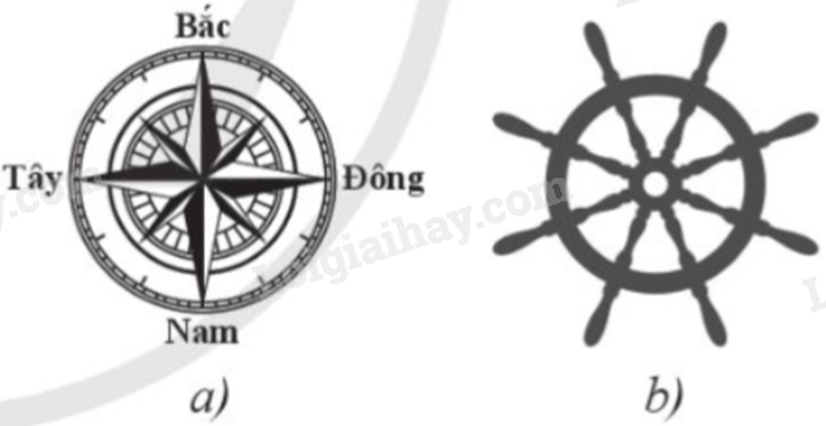
-
A.
thực hiện phép quay thuận chiều \(90^\circ \).
-
B.
thực hiện phép quay ngược chiều \(90^\circ \).
-
C.
thực hiện phép quay thuận chiều \(45^\circ \).
-
D.
thực hiện phép quay ngược chiều \(45^\circ \).
-
A.
\(P,{\mkern 1mu} {\mkern 1mu} N,{\mkern 1mu} {\mkern 1mu} M\).
-
B.
\(M,{\mkern 1mu} {\mkern 1mu} N,{\mkern 1mu} {\mkern 1mu} P\).
-
C.
\(M,{\mkern 1mu} {\mkern 1mu} N,{\mkern 1mu} {\mkern 1mu} P\).
-
D.
\(P,{\mkern 1mu} {\mkern 1mu} M,{\mkern 1mu} {\mkern 1mu} N\).
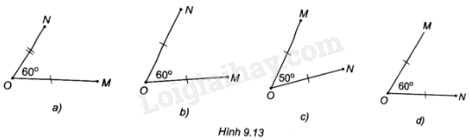
Hình nào dưới đây vẽ hai điểm M, N thỏa mãn phép quay ngược chiều \({60^o}\) tâm O biến N thành M?
Trên mặt phẳng toạ độ Oxy cho M(–4; 0), N(4; 0) và P(3; 3).
a) Phép quay ngược chiều α° tâm O biến điểm M thành điểm N. Tìm α.
b) Qua phép quay thuận chiều 90° tâm O, điểm P biến thành điểm nào?
a) Cho hình bình hành ABCD, O là giao điểm của hai đường chéo AC và BD. Chỉ ra phép quay ngược chiều tâm O sao cho phép quay đó biến mỗi điểm C và D thành điểm đối xứng với nó qua tâm O.
b) Cho lục giác đều A1A2A3A4A5A6 tâm O. Chỉ ra phép quay thuận chiều tâm O sao cho phép quay đó biến mỗi điểm A3, A4, A5 thành điểm đối xứng với nó qua tâm O.
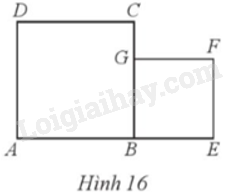
Cho hai hình vuông ABCD và BEFG (Hình 16).
a) Phép quay thuận chiều 90° tâm B biến các điểm A, B, G lần lượt thành các điểm nào?
b) Phép quay ngược chiều 45° tâm A biến các điểm B, E lần lượt thành các điểm nào?
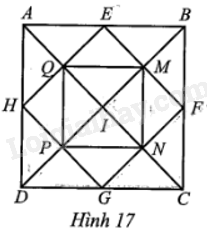
Cho hình vuông ABCD, I là giao điểm của hai đường chéo AC, BD. E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA. Q, N lần lượt là giao điểm của AC với HE và AC với GF; M, P lần lượt là giao điểm của BD với EF và BD với GH (Hình 17). Phép quay thuận chiều 90° tâm I có giữ nguyên các tứ giác EFGH và tứ giác MNPQ hay không? Vì sao?
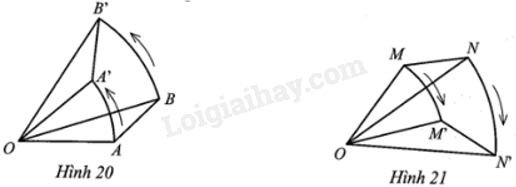
Cho điểm O cố định và số đo α° (0° < α° < 180°).
a) Ở Hình 20, phép quay ngược chiều α° tâm O biến điểm A thành điểm A’ và biến điểm B thành điểm B’. Chứng minh AB = A’B’.
b) Ở Hình 21, phép quay thuận chiều α° tâm O biến điểm M thành điểm M’ và biến điểm N thành điểm N’. Hỏi MN có bằng M’N’ hay không? Vì sao?
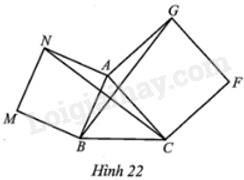
Cho tam giác ABC. Về phía ngoài tam giác đó dựng các hình vuông ABMN và ACFG (Hình 22). Sử dụng kết quả bài tập 21 chứng minh BG = CN.







Danh sách bình luận