Trên mặt phẳng, một vật nhỏ chuyển động trên đường tròn tâm \(O\) bán kính 2m, một vật nhỏ khác chuyển động trên đường thẳng \(a\) bằng 3m. Hai vật nhỏ có bao giờ gặp nhau không?
Dựa vào hệ thức giữa \(d\) và \(R\) để xác định.
Do \(3m > 2m \Rightarrow d > R\).
Vậy đường thẳng và đường tròn không giao nhau nên hai vật nhỏ không bao giờ gặp nhau.
Các bài tập cùng chuyên đề
Cho đường tròn $\left( O \right)$ và đường thẳng $a$. Kẻ $OH \bot a$ tại $H$, biết $OH > R$ khi đó đường thẳng $a$ và đường tròn $\left( O \right)$
Trên hình 5.35a, ta có OO’ > OA + OB, trên Hình 5.35b, ta có OO’ < OA – O’B. Trong mỗi trường hợp, hãy vẽ hai đường tròn (O; OA) và (O’; OB) và cho biết hai đường tròn đó có điểm chung nào không.
Trong Hình 25, cột thẳng đứng và biển quảng cáo có dạng hình tròn gợi nên hình ảnh của đường thẳng và đường tròn không giao nhau. Theo em, đường thẳng và đường tròn không giao nhau thì chúng có điểm chung hay không?
Quan sát Hình 26.
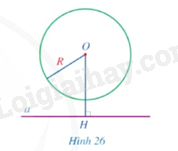
a) Cho biết đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) có bao nhiêu điểm chung.
b) So sánh độ dài đoạn thẳng \(OH\) và \(R\).
Cho đường tròn \(\left( O \right)\) và đường thẳng \(a\). Kẻ \(OH \bot a\) tại \(H\), biết \(OH < R,\) khi đó đường thẳng \(a\) và đường tròn \(\left( O \right)\)
