Trong Hình 30, mép ngoài cửa ra vào có dạng một phần của đường tròn bán kính 1,6m. Hãy tính chiều cao \(HK\) của cửa đó, biết \(AH = 0,9m\).
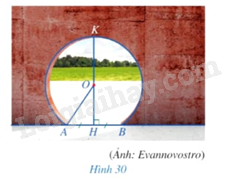
Áp dụng định lí Pythagore để tính.
Áp dụng định lý Pythagore vào tam giác \(AOH\) vuông tại \(H\), ta có:
\(A{O^2} = O{H^2} + A{H^2} \Rightarrow 1,{6^2} = O{H^2} + 0,{9^2} \Rightarrow OH = \frac{{\sqrt 7 }}{2}\left( m \right)\).
Chiều cao \(HK\) của cửa đó là: \(HK = OK + OH = 1,6 + \frac{{\sqrt 7 }}{2} \approx 2,9\left( m \right)\).
Các bài tập cùng chuyên đề
Đường thẳng và đường tròn có nhiều nhất bao nhiêu điểm chung
Cho hai đường tròn \(\left( {O;4cm} \right)\) và \(\left( {O';3cm} \right)\) biết \(OO' = 5cm\). Hai đường tròn trên cắt nhau tại \(A\) và \(B\). Độ dài \(AB\) là:
Đường thẳng \(a\) cách tâm \(O\) của đường tròn \(\left( {O;R} \right)\)một khoảng bằng \(\sqrt 8 \,\,cm.\) Biết \(R = 3\,\,cm,\) số giao điểm của đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) là:
Quan sát Hình 20.
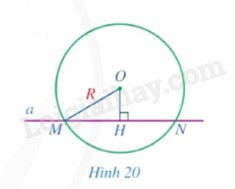
a) Cho biết đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\) có bao nhiêu điểm chung.
b) So sánh độ dài đoạn thẳng \(OH\) và \(R\).
Hãy chỉ ra một số hiện tượng trong thực tiễn gợi nên hình ảnh của đường thẳng và đường tròn cắt nhau.
Cho đường tròn tâm O bán kính R và một điểm A nằm trong (O) \(\left( {OA < R} \right)\). Vẽ đường thẳng a bất kì đi qua A. Xác định vị trí tương đối của đường thẳng a và đường tròn (O).
Cho đường thẳng a và điểm O với khoảng cách từ điểm O đến đường thẳng a là 1 cm. Vẽ đường tròn tâm O bán kính 3 cm.
a) Xác định vị trí tương đối của đường thẳng a và đường tròn (O).
b) Gọi A và B là các giao điểm của đường thẳng a và đường tròn (O). Tính độ dài đoạn thẳng AB.
Cho đường thẳng a và một điểm O cách a là 3cm. Vẽ đường tròn (O; 5cm). Gọi B, C là các giao điểm của đường thẳng a và (O). Diện tích của tam giác OBC bằng
A. \(10c{m^2}\).
B. \(6c{m^2}\).
C. \(24c{m^2}\).
D. \(12c{m^2}\).
