Cho tam giác \(ABC\) vuông tại \(A,AB = 3cm,BC = 5cm\). Đường thẳng \(AB\) có tiếp xúc với đường tròn \(\left( {C;4cm} \right)\) hay không? Vì sao?
Dựa vào kiến thức vừa học để chứng minh.
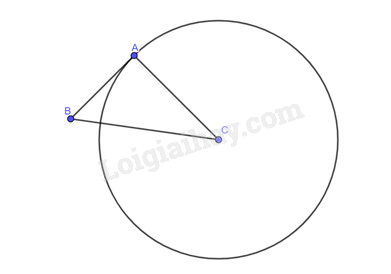
Xét tam giác \(ABC\) vuông tại \(A\), áp dụng định lí Pythagore ta có:
\(A{B^2} + A{C^2} = B{C^2} \Rightarrow {3^2} + A{C^2} = {5^2} \Rightarrow AC = 4\left( {cm} \right)\).
Vậy đường thẳng \(AB\) có tiếp xúc với đường tròn \(\left( {C;4cm} \right)\).
Các bài tập cùng chuyên đề
Nếu đường thẳng và đường tròn có duy nhất một điểm chung thì
Cho hai điểm O và O’ sao cho OO’ = 3 cm. Giải thích tại sao hai đường tròn (O; 8 cm) và (O’; 5 cm) tiếp xúc với nhau. Chúng tiếp xúc trong hay tiếp xúc ngoài?
Một diễn viên xiếc đi xe đạp một bánh trên sợi dây cáp căng được cố định ở hai đầu dây. Biết đường kính bánh xe là 72 cm, tính khoảng cách từ trục bánh xe đến dây cáp.
Trong bức ảnh ở Hình 22, sợi dây dưới cùng và bánh xe gợi nên hình ảnh đường thẳng và đường tròn tiếp xúc nhau. Theo em, đường thẳng và đường tròn đó có bao nhiêu điểm chung?
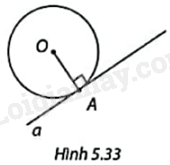
Trong Hình 5.33, đường tròn (O) có bán kính R và điểm A nằm trên đường tròn, đường thẳng a vuông góc với OA tại A. So sánh khoảng cách từ O đến đường thẳng a với bán kính R, từ đó xác định vị trí tương đối của a và (O).
Đường thẳng d tiếp xúc với đường tròn tâm O đường kính 8cm. Khoảng cách từ tâm O đến đường thẳng d là
A. 4cm.
B. 8cm.
C. 12cm.
D. 16cm.
Nếu đường thẳng và đường tròn có hai điểm chung thì
Cho $a,b$ là hai đường thẳng song song và cách nhau một khoảng $2,5\,cm$. Lấy điểm $I$ trên $a$ và vẽ đường tròn $\left( {I;2,5cm} \right)$. Khi đó đường tròn với đường thẳng $b$
Cho \(a,b\) là hai đường thẳng song song và cách nhau một khoảng \(3\,cm\). Lấy điểm \(I\) trên \(a\) và vẽ đường tròn \(\left( {I;3,5cm} \right)\). Khi đó đường tròn với đường thẳng \(b\)
Cho góc $\widehat {xOy}\,\left( {0 < \widehat {xOy} < 180^\circ } \right)$. Đường tròn $\left( I \right)$ là đường tròn tiếp xúc với cả hai cạnh $Ox;Oy$. Khi đó điểm $I$ chạy trên đường nào?
Cho hai đường thẳng $a$ và $b$ song song với nhau, cách nhau một khoảng là $h$. Một đường tròn $\left( O \right)$ tiếp xúc với $a$ và $b$. Hỏi tâm $O$ di động trên đường nào?
Cho hai đường thẳng \(a\) và \(b\) song song với nhau, cách nhau một khoảng là \(6\,cm\). Một đường tròn \(\left( O \right)\) tiếp xúc với \(a\) và \(b\). Hỏi tâm \(O\) di động trên đường nào?
Cho đường thẳng a, điểm M thuộc a và số dương R.
Vẽ đường thẳng b đi qua M và vuông góc với a. Trên b xác định điểm A sao cho \(AM = R\) (đvđd). Chứng minh rằng đường tròn (A; R) tiếp xúc với a tại M. Ta có thể vẽ được mấy đường tròn như thế?
Cho tam giác ABC vuông tại A, đường cao AH. Từ B và từ C kẻ hai đường thẳng tiếp xúc với đường tròn (A; AH) lần lượt tại D và E. Chứng minh rằng:
a) Hai điểm D và E đối xứng với nhau qua A;
b) DE tiếp xúc với đường tròn đường kính BC.
Cho góc vuông xOy có hai cạnh tiếp xúc với đường tròn (I; R) tại A, B. Cho biết chu vi của tứ giác OAIB bằng 20 cm. Tính R và độ dài AB.
Cho hình thang vuông ABCD (\(\widehat A = \widehat D = 90^\circ \)) có AB = 4 cm, BC = 13 cm, CD = 9 cm.
a) Tính độ dài đoạn thẳng AD.
b) Đường thẳng AD có tiếp xúc với đường tròn đường kính BC hay không? Vì sao?
Trên mặt phẳng toạ độ Oxy, cho điểm A(1; 1). Khi đó, đường tròn (A;1)
A. Tiếp xúc với trục Ox và cắt trục Oy tại 2 điểm phân biệt.
B. Tiếp xúc với trục Oy và cắt trục Ox tại 2 điểm phân biệt.
C. Tiếp xúc với cả hai trục Ox và trục Oy.
D. Đi qua gốc toạ độ O.
Cho đường tròn (O) đường kính AB, tiếp tuyến xx’ tại A và tiếp tuyến yy’ tại B của (O). Một tiếp tuyến thứ ba của (O) tại điểm P (P khác A và B) cắt xx’ tại M và cắt yy’ tại N.
a) Chứng minh rằng \(MN = MA + NB\).
b) Đường thẳng đi qua O và vuông góc với AB cắt MN tại Q. Chứng minh rằng Q là trung điểm của đoạn MN.
c) Chứng minh rằng AB tiếp xúc với đường tròn đường kính MN.
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A và cùng tiếp xúc với đường thẳng d tại B và C (khác A), trong đó \(B \in \left( O \right)\) và \(C \in \left( {O'} \right)\). Tiếp tuyến của (O) tại A cắt BC tại M. Chứng minh rằng:
a) Đường thẳng MA tiếp xúc với (O’);
b) Điểm M là trung điểm của đoạn thẳng BC từ đó suy ra ABC là tam giác vuông.
