Một quả bóng rổ (khi bơm căng) có đường kính 24 cm (Hình 14). Tìm thể tích của quả bóng rổ đó (kết quả làm tròn đến hàng đơn vị).

Dựa vào công thức thể tích của hình cầu có bán kính R là: V = \(\frac{4}{3}\pi {R^3}\).
Bán kính quả bóng là: R = \(\frac{d}{2} = \frac{{24}}{2}\) = 12 cm.
Thể tích của quả bóng rổ là: V = \(\frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.12^3} \approx \) 7238 (cm3).

Các bài tập cùng chuyên đề
Sử dụng một hình cầu bán kính R và một cốc thủy tinh có dạng hình trụ bán kính đáy R, chiều cao 2R. Ban đầu để hình cầu nằm khít trong chiếc cốc đầy nước. Ta nhấc hình cầu ra khỏi cốc thủy tinh hình trụ (H.10.25).
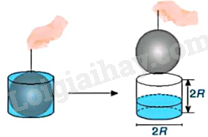
Đo độ cao cột nước còn lại trong chiếc cốc, ta thấy độ cao này chỉ bằng \(\frac{1}{3}\) chiều cao của chiếc cốc hình trụ. Từ đó, em hãy dự đoán công thức tính thể tích hình cầu bán kính R.
Em hãy trả lời câu hỏi của tình huống mở đầu.
Quả bóng đá theo tiêu chuẩn FIFA (liên đoàn bóng đá thế giới) có dạng hình cầu với đường kính khoảng 22cm (H.10.18). Khi bơm căng quả bóng thì thể tích quả bóng bằng bao nhiêu?

Người ta nhấn chìm hoàn toàn 5 viên bi có dạng hình cầu vào một chiếc cốc hình trụ đựng đầy nước, mỗi viên bi có đường kính 2cm. Tính lượng nước tràn ra khỏi cốc.
Một mặt phẳng đi qua tâm hình cầu, cắt hình cầu theo một hình tròn có diện tích \(9\pi \;c{m^2}\). Thể tích của hình cầu bằng
A. \(972\pi \;c{m^3}\).
B. \(36\pi \;c{m^3}\).
C. \(6\pi \;c{m^3}\).
D. \(81\pi \;c{m^3}\).
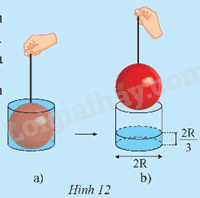
Một quả cầu có bán kính R nằm khít trong chiếc bình hình trụ đổ đầy nước có chiều cao h = 2R (Hình 12a). Rút qua cầu ra khỏi bình nước, ta thấy chiều cao của mực nước bằng \(\frac{1}{3}\) chiều cao h (Hình 12b). Hãy tính theo R:
a) Thể tích của chiếc bình hình trụ;
b) Thể tích của nước ở trong bình;
c) Thể tích của hình cầu.
Thể tích của hình cầu có bán kính 12 cm là
A. 120\(\pi \)cm3.
B. 2304\(\pi \)cm3.
C. 1000\(\pi \)cm3.
D. 2304\(\pi \)cm3.
Cho một hình cầu bán kính R và một cốc thuỷ tỉnh có dạng hình trụ với bán kính đáy là R, chiều cao là 2R.
Đặt hình cầu nằm khít trong cốc hình trụ rồi đổ đầy nước vào cốc đó (Hình 36a). Nhấc nhẹ hình cầu ra khỏi cốc. Đo độ cao cột nước còn lại, ta thấy độ cao này chỉ bằng \(\frac{1}{3}\) chiều cao của cốc (Hình 36b). Hãy cho biết thể tích của hình cầu bằng bao nhiêu phần thể tích của cốc hình trụ.

Một bình nuôi cá cảnh có dạng hình cầu với đường kính khoảng 40 cm. Người ta muốn đổ vào bình nuôi cá đó một lượng nước bằng một nửa thể tích của bình (Hình 39). Hỏi cần phải đổ vào bình bao nhiêu lít nước (làm tròn kết quả đến hàng phần mười)?

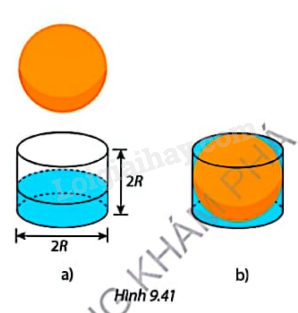
Bạn Mai thả từ từ một quả cầu bán kính R vào một chiếc cốc thuỷ tinh hình trụ chứa sẵn nước đến \(\frac{1}{3}\) chiều cao cốc (Hình 9.41a) thì thấy nước dâng lên vừa miệng cốc (Hình 9.41b). Dựa vào kết quả thí nghiệm của bạn Mai, viết công thức tính:
a) Thể tích của chiếc cốc hình trụ theo R
b) Thể tích của quả cầu.
Tính bán kính của một quả địa cầu có thể tích 14130 cm3, lấy \(\pi \approx 3,14\).

Hãy trả lời câu hỏi ở phần Khởi động.
Phần Khởi động: Bán kính Sao Mộc gấp khoảng 11 lần bán kính Trái Đất. Vậy thể tích Sao Mộc gấp bao nhiêu lần thể tích Trái Đất?
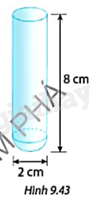
Tính diện tích bề mặt ngoài và thể tích của một ống nghiệm có phần thân hình trụ và đáy là nửa hình cầu với kích thước như Hình 9.43.
Người ta dùng các vòng tròn bằng kẽm có bán kính 12,5 cm làm khung cho đèn treo hình cầu (Hình 9.45). các vòng kẽm đều là các đường tròn lớn của hình cầu này. Tính thể tích của đèn treo.

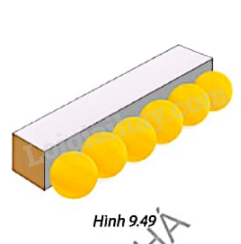
Một công ty thiết kế mẫu hộp làm từ bìa mỏng dạng hình hộp chữ nhật để đóng gói 6 quả bóng bàn có thông số kĩ thuật \(\phi \)40 (đường kính bóng là 40 mm) (Hình 9.49).
a) Tính diện tích xung quanh của hộp, biết rằng đáy hộp là hình vuông cạnh 40 mm và chiều cao của hộp vừa đủ để xếp khít 6 quả bóng bàn.
b) Tính thể tích phần không gian trống của hộp khi chứa 6 quả bóng bàn.
Thể tích của hình cầu có bán kính 6 dm bằng
A. 288 dm3
B. 288\(\pi \)dm3
C. 144\(\pi \)dm3
D. 144\(\pi \) dm3
Cho hình cầu có thể tích \(V = 288\pi (c{m^3})\). Tính đường kính mặt cầu của hình cầu đó.
-
A.
6cm.
-
B.
12cm.
-
C.
8cm.
-
D.
16cm.
Một bình chia độ hình trụ chứa 200 cm3 nước. Người ta bỏ lọt vào bình và chìm trong nước một khối kim loại hình cầu. Khi nước yên lặng, người ta thấy nước dâng lên vạch 313,04 cm3. Bán kính của khối kim loại hình cầu là: (Lấy \(\pi \approx 3,14\)).
-
A.
1cm.
-
B.
2cm.
-
C.
3cm.
-
D.
4cm.
Cuối tuần bạn An tự thưởng cho mình một cốc trà sữa trân châu tự làm. An cho \(10\) viên trân châu hình cầu có đường kính mỗi viên \(0,6\,cm\) cùng với lượng trà sữa vào \(\frac{3}{4}\) cốc thủy tinh. Biết cốc thủy tinh dạng hình trụ có bán kính đáy \(3\,cm\), chiều cao cốc là \(12\,cm\). Hỏi thể tích lượng trà sữa An cần rót vào cốc là bao nhiêu \(c{m^3}\)? (Lấy \(\pi \approx 3,14\) và kết quả làm tròn đến hàng đơn vị)
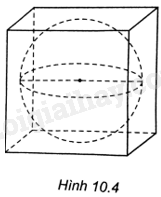
Một chiếc hộp hình lập phương có cạnh bằng 18cm đựng vừa khít một quả bóng hình cầu (H.10.4). Tính thể tích của quả bóng (coi độ dày của hộp không đáng kể).
Gọi R là bán kính, S là diện tích mặt cầu và V là thể tích của hình cầu. Công thức nào sau đây là sai?
A. \(3V = SR\).
B. \(S = 4\pi {R^2}\).
C. \(V = \frac{4}{3}\pi {R^3}\).
D. \(S = \pi {R^2}\).
Một mặt cầu có diện tích \(36\pi \,{m^2}\). Thể tích của hình cầu này là
A. \(V = \frac{4}{3}\pi \;{m^3}\).
B. \(V = 36\pi \;{m^3}\).
C. \(V = 72\pi \;{m^3}\).
D. \(V = 108\pi \;{m^3}\).
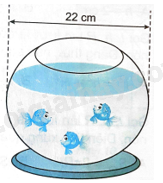
Bạn Khôi có một chiếc bể cá làm bằng thủy tinh, có dạng hình cầu, đường kính 22cm. Khi nuôi cá, Khôi thường đổ vào bể lượng nước có thể tích bằng \(\frac{2}{3}\) thể tích của bể. Tính thể tích nước bạn Khôi đổ vào bể khi nuôi cá (làm tròn kết quả đến hàng đơn vị của \(c{m^3}\)).
Trái Đất là một quả cầu khổng lồ có thể tích khoảng 1086,23.\({10^9}k{m^3}\). Sử dụng công thức tính thể tích hình cầu, hãy cho biết chiều dài đường xích đạo Trái Đất dài khoảng bao nhiêu kilômét (làm tròn kết quả đến hàng đơn vị của km)?
Cho biết 1 cm3 thép có khối lượng là 7,85 g. Với 2 kg thép thì chế tạo được bao nhiêu viên bi đặc dạng hình cầu có bán kính 0,8 cm (bỏ qua hao hụt trong quá trình chế tạo)?
Một quả bida có dạng hình cầu với thể tích bằng 36 000π mm3. Hỏi đường kính của quả bida đó bằng bao nhiêu centimét?
Người ta thả một viên bi có dạng hình cầu (đặc, không thấm nước) với bán kính là 3 cm vào một cái cốc dạng hình trụ chứa nước. Người ta thấy viên bi chìm xuống đáy cốc và chiều cao mực nước dâng thêm 1,5 cm. Biết chiều cao của mực nước ban đầu trong cốc bằng 7,2 cm. Tính thể tích của khối nước ban đầu trong cốc (theo đơn vị centimét khối và làm tròn kết quả đến hàng phần mười).
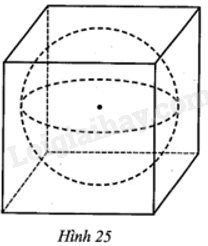
Người ta đổ đầy nước vào một bể hình lập phương cạnh 2a. Tiếp theo, người ta thả vào trong bể đó một vật thể có dạng hình cầu (đặc, không thấm nước) bán kính a như Hình 25. Hỏi lượng nước còn lại trong bể bằng bao nhiêu phần trăm lượng nước bị trào ra khỏi bể (làm tròn kết quả đến hàng phần mười)?
Thể tích của một hình cầu bằng \(\frac{\pi }{6}\) dm3. Đường kính của hình cầu đó là:
A. 2 dm.
B. \(\frac{3}{2}\) dm
C. 1 dm
D. \(\frac{1}{2}\) dm
Cần bao nhiêu lít nước để đổ đầy \(\frac{3}{4}\) một bình nuôi cá cảnh? Biết bình nuôi cá cảnh đó có dạng một phần hình cầu và có thể tích bằng \(\frac{5}{6}\) thể tích một hình cầu có đường kính là 30 cm.
Một cốc nước có dạng hình trụ chiều cao 20 cm, bán kính đáy là 4 cm, lượng nước ban đầu trong cốc cao 9 cm. Người ta thả chìm vào cốc nước đó 4 viên bi thuỷ tinh hình cầu có cùng bán kính là 3 cm. Hỏi sau khi thả vào cốc nước 4 viên bi thuỷ tinh trên, mực nước trong cốc cách miệng cốc bao nhiêu centimét?







Danh sách bình luận