Một chiếc hộp chứa 1 tấm thẻ màu xanh, 1 tấm thẻ màu vàng và 1 tấm thẻ màu hồng. Các tấm thẻ có cùng kích thước và khối lượng. Bạn Hương lần lượt lấy ra ngẫu nhiên từng tấm thẻ từ trong hộp cho đến khi hộp hết thẻ.
a) Xác định không gian mẫu của phép thử.
b) Tính xác suất của mỗi biến cố sau:
A: “Tấm thẻ màu hồng được lấy ra đầu tiên”;
B: “Tấm thẻ màu xanh được lấy ra trước tấm thẻ màu vàng”;
C: “Tấm thẻ lấy ra lần cuối cùng không có màu xanh”.
- Dựa vào khái niệm không gian mẫu, kí hiệu là \(\Omega \), là tập hợp tất cả các kết quả có thể xảy ra của phép thử.
- Tính các kết quả thuận lợi của biến cố.
- Sau đó tính xác suất các biến cố dựa vào: Xác suất của biến cố A, kí hiệu là P(A), được xác định bởi công thức: \(P(A) = \frac{{n(A)}}{{n(\Omega )}}\), trong đó n(A) là số các kết quả thuận lợi cho A; \(n(\Omega )\) là số các kết quả có thể xảy ra.
a) Không gian mẫu của phép thử: \(\Omega \) = {XVH, XHV, HVX, HXV, VHX, VXH}
Suy ra \(n(\Omega )\) = 6.
b) Vì các thẻ có cùng kích thước và khối lượng nên có cùng khả năng được chọn.
Có 2 kết quả thuận lợi cho biến cố A là: HVX, HXV.
Xác suất xảy ra biến cố A là: P(A) = \(\frac{2}{6} = \frac{1}{3}\).
Có 3 kết quả thuận lợi cho biến cố B là: XVH, XHV, HXV.
Xác suất xảy ra biến cố B là: P(B) = \(\frac{3}{6} = \frac{1}{2}\).
Có 4 kết quả thuận lợi cho biến cố C là: XVH, XHV, HXV, VXH.
Xác suất xảy ra biến cố C là: P(C) = \(\frac{4}{6} = \frac{2}{3}\).
Các bài tập cùng chuyên đề
Trên một dãy phố có ba quán ăn A, B, C. Hai bạn Văn và Hải mỗi người chọn ngẫu nhiên một quán ăn để ăn trưa.
a) Mô tả không gian mẫu của phép thử.
b) Tính xác suất của các biến cố sau:
E: “Hai bạn cùng vào một quán”;
F: “Cả hai bạn không chọn quán C”;
G: “Có ít nhất một bạn chọn quán B”.
Một nhóm của lớp 9A có 3 bạn nam và 2 bạn nữ. Giáo viên chọn ngẫu nhiên 2 bạn trong nhóm để tham gia một phong trào của trường.
a) Mô tả không gian mẫu.
b) Tính xác suất để hai bạn được chọn khác giới.
Một hộp chứa 1 quả bóng màu vàng, 1 quả bóng màu trắng và 1 quả bóng màu cam. Các quả bóng có cùng kích thước và khối lượng. Bạn Ánh lấy ra ngẫu nhiên lần lượt 2 quả bóng từ hộp.
a) Số phần tử của không gian mẫu của phép thử là
A. 3.
B. 4.
C. 5.
D. 6.
b) Xác suất của biến cố “Có 1 quả bóng màu vàng trong 2 quả bóng lấy ra” là
A. 0.
B. \(\frac{1}{3}\)
C. \(\frac{1}{2}\)
D. \(\frac{2}{3}\)
c) Xác suất của biến cố “Không quả bóng màu xanh trong 2 quả bóng lấy ra” là
A. 0.
B. \(\frac{1}{3}\)
C. \(\frac{2}{3}\)
D. 1.
d) Xác suất của biến cố “Quả bóng lấy ra đầu tiên là quả bóng màu trắng” là
A. 0.
B. \(\frac{1}{3}\)
C. \(\frac{2}{3}\)
D. 1.
e) Xác suất của biến cố “Quả bóng lấy ra lần thứ hai không phải là quả bóng màu cam” là
A. 0.
B. \(\frac{1}{3}\)
C. \(\frac{2}{3}\)
D. 1.
Bạn Giang gieo một con xúc xắc cân đối và đồng chất hai lần liên tiếp.
a) Số phần tử của không gian mẫu của phép thử là
A. 6.
B. 12.
C. 30.
D. 36.
b) Số kết quả thuận lợi cho biến cố “Tổng số chấm xuất hiện là 4” là
A. 2.
B. 3.
C. 4.
D. 5.
c) Xác suất của biến cố “Lần gieo thứ hai xuất hiện mặt 5 chấm” là
A. \(\frac{1}{6}\)
B. \(\frac{1}{{36}}\)
C. \(\frac{2}{3}\)
D. \(\frac{1}{5}\)
d) Xác suất của biến cố “Có đúng 1 lần xuất hiện mặt 6 chấm” là
A. \(\frac{1}{6}\)
B. \(\frac{5}{{18}}\)
C. \(\frac{{11}}{{36}}\)
D. \(\frac{1}{3}\)
e) Xác suất của biến cố “Tích số chấm xuất hiện của hai lần gieo là số lẻ” là
A. \(\frac{1}{4}\)
B. \(\frac{1}{3}\)
C. \(\frac{1}{2}\)
D. \(\frac{3}{4}\)
Bạn Trang chọn ngẫu nhiên một số tự nhiên có ba chữ số.
a) Xác định không gian mẫu của phép thử.
b) Xác định tập hợp các kết quả thuận lợi cho các biến cố sau và tính xác suất của mỗi biến cố đó.
A: “Số được chọn là lập phương của một số tự nhiên”;
B: “Số được chọn nhỏ hơn 500”.
Gieo hai con xúc xắc cân đối và đồng chất. Tính xác suất của mỗi biến cố sau:
A: “Tích số chấm xuất hiện trên hai con xúc xắc bằng 12”;
B: “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 8”.
Một hộp chứa 5 tấm thẻ cùng loại được đánh số lần lượt là 1; 4; 9; 10; 16. Lấy ngẫu nhiên đồng thời 2 tấm thẻ từ hộp.
a) Xác định không gian mẫu và số kết quả có thể xảy ra của phép thử.
b) Tính xác suất của mỗi biến cố sau:
A: “Tích các số ghi trên 2 tấm thẻ chia hết cho 5”;
B: “Tổng các số ghi trên 2 tấm thẻ lớn hơn 14”.
Hình 27 mô tả một đĩa tròn bằng bìa cứng được chia làm 12 phần bằng nhau và ghi các số 1,2,3,…,12; chiếc kim được gắn cố định vào trục quay ở tâm của đĩa.
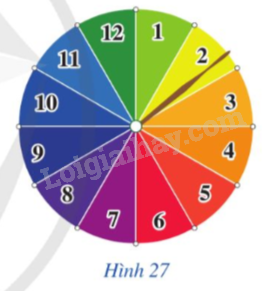
Xét phép thử "Quay đĩa tròn một lần”.
a) Viết tập hợp Ω gồm các kết quả có thể xảy ra đối với số ghi ở hình quạt mà chiếc kim chỉ vào khi đĩa dừng lại.
b) Liệt kê các kết quả thuận lợi cho biến cố A: “Chiếc kim chỉ vào hình quạt ghi số chia hết cho 3”.
c) Tìm tỉ số giữa số các kết quả thuận lợi cho biến cố A và số phần tử của tập hợp Ω.
Một hộp có 20 viên bi với kích thước và khối lượng như nhau. Bạn Ngân viết lên các viên bi đó các số 1, 2, 3, 4, …, 20; hai viên bi khác nhau thì viết hai số khác nhau.
Xét phép thử “Lấy ngẫu nhiên một viên bi trong hộp”.
a) Liệt kê các kết quả có thể xảy ra đối với số xuất hiện trên viên bi được lấy ra.
b) Viết không gian mẫu của phép thử đó
c) Tính xác suất của biến cố: “Số xuất hiện trên viên bi được lấy ra chia cho 7 dư 1”.
Viết ngẫu nhiên một số tự nhiên lớn hơn 499 và nhỏ hơn 1000.
a) Có tất cả bao nhiêu kết quả có thể xảy ra ở phép thử trên.
b) Tính xác suất của mỗi biến cố sau:
A: “Số tự nhiên được viết ra chia hết cho 100”.
B: “Số tự nhiên được viết ra là lập phương của một số tự nhiên”.
Nhóm hoc sinh tình nguyện khối 9 của một trường THCS có 6 bạn, trong đó có 3 bạn nam là: Trung (lớp 9A), Quý (lớp 9A), Việt (lớp 9C) và 3 bạn nữ là: An (lớp 9A), Châu (lớp 9B), Hương (lớp 9D). Chọn ngẫu nhiên một bạn trong nhóm đó để tham gia hoạt động tình nguyện của trường.
a) Liệt kê tất cả các kết quả có thể xảy ra của phép thử trên. Có tất cả bao nhiêu kết quả có thể xảy ra?
b) Tính xác suất của mỗi biến cố sau:
A: “Bạn được chọn ra là bạn nữ”.
B: “Bạn được chọn ra thuộc lớp 9A”.
Trên mặt phẳng cho 5 điểm phân biệt A, B, C, D, E trong đó không có 3 điểm nào thẳng hàng. Hai điểm A, B được tô màu đỏ, ba điểm C, D, E được tô màu xanh. Bạn Châu chọn ra ngẫu nhiên một điểm tô màu đỏ và một điểm tô màu xanh (trong 5 điểm đó) để nối thành một đoạn thẳng.
a) Liệt kê các cách chọn mà bạn Châu có thể thực hiện.
b) Tính xác suất của biến cố sau:
P: “Trong 2 điểm được chọn ra, có điểm A”.
Q: “Trong 2 điểm được chọn ra, không có điểm C”.
Một bó hoa gồm 3 bông hoa màu đỏ và 1 bông hoa màu vàng. Bạn Linh chọn ngẫu nhiên 2 bông hoa từ bó hoa đó.
a) Liệt kê các cách chọn mà bạn Linh có thể thực hiện.
b) Tính xác suất của mỗi biến cố sau:
P: “Trong 2 bông hoa được chọn ra, có đúng 1 bông hoa màu đỏ”.
Q: “Trong 2 bông hoa được chọn ra, có ít nhất 1 bông hoa màu đỏ”.
Bạn Mai tạo danh sách gồm những bài hát mình yêu thích trên một ứng dụng nghe nhạc. Danh sách của Mai gồm 7 bài hát tiếng Việt, 4 bài hát tiếng Anh, 6 bài hát tiếng Pháp. Mỗi lần nghe nhạc, Mai mở danh sách và chọn chế độ phát ngẫu nhiên. Theo chế độ này, ứng dụng nghe nhạc sẽ bắt đầu từ một bài chọn ngẫu nhiên trong danh sách.
a) Xác định không gian mẫu của phép thử chọn ngẫu nhiên một bài hát.
b) Khả năng mỗi bài được chọn có như nhau không?
c) Liệt kê các kết quả thuận lợi cho biến cố A: “Bài bắt đầu là một bài hát tiếng Pháp”
d) Chép lại câu sau và tìm số thích hợp cho các ô ?:
“Có ? trên ? kết quả để biến cố A xảy ra”.
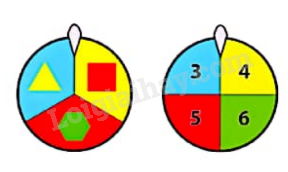
Bạn Huệ quay hai vòng tròn như hình dưới và ghi lại kết quả nhận được.
a) Hãy cho biết các phần tử của không gian mẫu.
b) Bạn Huệ quan tâm đến biến cố A: “Số cạnh của đa giác nhận được ở bánh xe thứ nhất bằng số tự nhiên nhận được từ bánh xe thứ hai”. Hỏi trong mỗi lần bạn Huệ quay hai bánh xe, xác suất để biến cố A xảy ra là bao nhiêu?
Viết ngẫu nhiên một số tự nhiên có hai chữ số không nhỏ hơn 80.
a) Viết tập hợp Ω gồm các kết quả có thể xảy ra đối với số tự nhiên được viết ra.
b) Tính xác suất của mỗi biến cố sau:
A: "Số tự nhiên được viết ra có chữ số hàng chục lớn hơn chữ số hàng đơn vị”;
B: "Số tự nhiên được viết ra có chữ số hàng chục gấp hai hoặc gấp ba lần chữ số hàng đơn vị".
Viết ngẫu nhiên một số tự nhiên có ba chữ số nhỏ hơn 400.
a) Tính số phần tử của tập hợp Ω gồm các kết quả có thể xảy ra đối với số tự nhiên được viết ra.
b) Tính xác suất của mỗi biến cố sau:
A: “Số tự nhiên được viết ra là lập phương của một số tự nhiên".
B: “Số tự nhiên được viết ra là số tự nhiên nhỏ nhất và khi chia số đó cho 5; 6; 7 có số dư lần lượt là 3; 2; 1".
Một đội học sinh gồm 7 bạn tham gia cuộc thi “An toàn giao thông cho học sinh trung học cơ sở do nhà trường tổ chức. Trong đó có 5 bạn học sinh lớp 9 là: An (lớp 9A), Bình (lớp 9A), Bảo (lớp 9B), Bách (lớp 9D), Lâm (lớp 9E) và 4 bạn học sinh lớp 8 là: Minh (lớp 8A), Hà (lớp 8B), Ngọc (lớp 8C), Lan (lớp 8E). Chọn ngẫu nhiên một thí sinh trong đội học sinh tham gia cuộc thi đó.
a) Liệt kê các cách chọn có thể thực hiện được. Có tất cả bao nhiêu kết quả có thể xảy ra?
b) Tính xác suất của mỗi biến cố sau:
A: “Thí sinh được chọn là học sinh lớp 8";
B: “Thí sinh được chọn là học sinh lớp 9A".
