Một bồn chứa xăng gồm hai nửa hình cầu có đường kính bằng 1,8m và một hình trụ có chiều cao bằng 3,6m (H.10.32). Tính thể tích của bồn chứa xăng (làm tròn kết quả đến hàng phần trăm của \({m^3}\)).
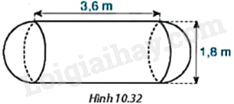
+ Bán kính hai nửa hình cầu là \(\frac{{1,8}}{2} = 0,9\left( m \right)\).
+ Tính thể tích \({V_1}\) hình trụ chiều cao 3,6m và bán kính 0,9m.
+ Tính thể tích \({V_2}\) hai nửa hình cầu bán kính 0,9m.
+ Thể tích bồn chứa xăng: \(V = {V_1} + {V_2}\).
Bán kính hai nửa hình cầu là \(\frac{{1,8}}{2} = 0,9\left( m \right)\).
Thể tích hình trụ chiều cao 3,6m và bán kính 0,9m là:
\({V_1} = \pi .0,{9^2}.3,6 = 2,916\pi \left( {{m^3}} \right)\).
Thể thể tích hai nửa hình cầu bán kính 0,9m là:
\({V_2} = \frac{4}{3}.\pi .0,{9^3} = 0,972\pi \left( {{m^3}} \right)\).
Thể tích bồn chứa xăng là:
\(V = {V_1} + {V_2} = 2,916\pi + 0,972\pi = 3,888\pi \approx 12,21\left( {{m^3}} \right)\).

Các bài tập cùng chuyên đề
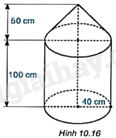
Một dụng cụ gồm một phần có dạng hình trụ và một phần có dạng hình nón với các kích thước như Hình 10.16.
a) Tính thể tích của dụng cụ này.
b) Tính diện tích mặt ngoài của dụng cụ (không tính đáy của dụng cụ).
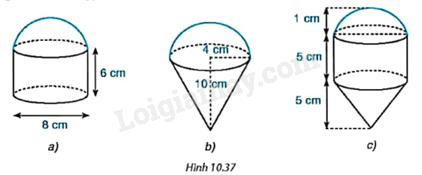
Các hình dưới đây (H.10.37) được tạo thành từ các nửa hình cầu, hình trụ và hình nón (có cùng bán kính đáy). Tính thể tích của các hình đó theo kích thước đã cho.
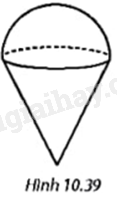
Một chiếc kem ốc quế gồm hai phần: Phần phía dưới dạng hình nón có chiều cao gấp đôi bán kính đáy, phần trên là nửa hình cầu có đường kính bằng đường kính đáy của hình nón phía dưới (H.10.39). Thể tích phần kem phía trên bằng \(200c{m^3}\). Tính thể tích của cả chiếc kem.
Trong các đồ vật sau, đồ vật nào có hình trụ, hình nón, hình cầu?
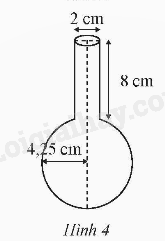
Ta coi một ống nghiệm có phần trên là hình trụ và phần dưới là hình cầu (Hình 4). Hãy tính thể tích nước cần để đổ đầy vào ống nghiệm, coi bề dày của ống nghiệm không đáng kể.
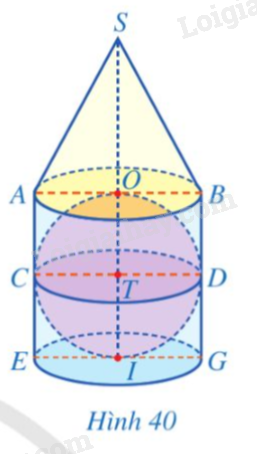
Hình 40 gồm một hình cầu đặt nằm khít trong hình trụ, một hình nón có mặt đáy là mặt đáy trên của hình trụ và đặt phía trên hình trụ. Quan sát Hình 40, hãy chỉ ra:
a) Bốn bán kính đáy, hai đường sinh và chiều cao của hình trụ;
b) Đỉnh, hai bán kính đáy, hai đường sinh và chiều cao của hình nón;
c) Tâm, hai đường kính, bốn bán kính và một hình tròn lớn của hình cầu.
Một kho chứa ngũ cốc có dạng một hình trụ và một mái vòm có dạng nửa hình cầu. Phần hình trụ có đường kính đáy là 10 m và chiều cao là 12 m. Phần mái vòm là nửa hình cầu đường kính 10 m (Hình 42). Hỏi dung tích của kho đó là bao nhiêu mét khối (bỏ qua bề dày của tường nhà kho và làm tròn kết quả đến hàng phần trăm)? (lấy \(\pi \approx 3,14\))

Cho một hình trụ và một hình nón có cùng bán kính đáy là r và cùng chiều cao là h.
Hình nào trong hai hình đã cho có thể tích lớn hơn?
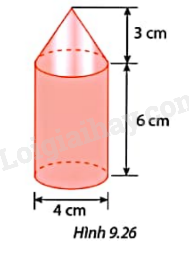
Tính thể tích của mô hình tên lửa trong Hình 9.26.
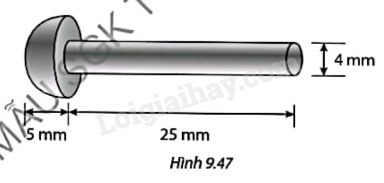
Tính khối lượng thép cần dùng để sản xuất 1000 chiếc đinh tán có thân hình trụ và đầu là nửa hình cầu với kích thước như Hình 9.47, biết khối lượng riêng của thép là 7850 kg/m3.
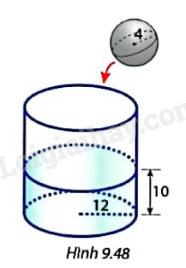
Một chiếc cốc hình trụ có phần đáy bên trong là một hình tròn bán kính bằng 12 cm. Chiều cao của mực nước trong cốc là 10 cm (Hình 9.48).
a) Tính thể tích nước trong cốc.
b) Thả một quả cầu bằng kim loại có bán kính 4 cm vào cốc cho đến khi quả cầu chìm hẳn xuống đáy cốc và mực nước đứng yên. Hỏi mực nước trong cốc tăng thêm bao nhiêu centimet?
a) Diện tích xung quanh của hình nón, hình trụ sẽ thay đổi như thế nào nếu bán kính không đổi còn độ dài đường sinh tăng gấp ba lần?
b) Thể tích hình nón, hình trụ sẽ thay đổi như thế nào nếu bán kính đáy tăng gấp đôi còn chiều cao không đổi?
c) Diện tích mặt cầu và thể tích hình cầu sẽ thay đổi như thế nào nếu bán kính hình cầu giảm một nửa?
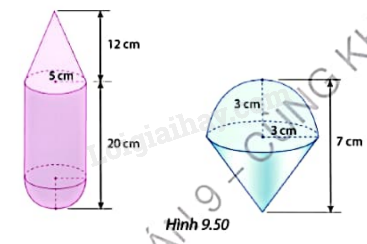
Tính thể tích của mỗi hình ở Hình 9.50.
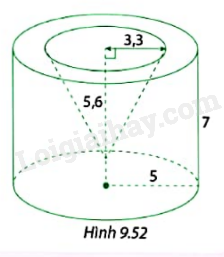
Từ một khối gỗ hình trụ bán kính đáy 5 cm và cao 7 cm, người ta khoét đi một phần gỗ của hình nón có bán kính đáy 3,3 cm và chiều cao 5,6 cm (Hình 9,25). Tính thể tích phần còn lại của khối gỗ.
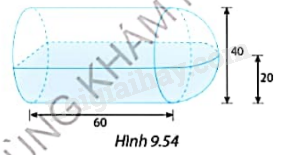
Một bình nước dạng hình trụ kết hợp với nửa hình cầu có kích thước như Hình 9.54. Khi bình nước nằm ngang, mực nước trong bình cao 20 cm.
a) Tính thể tích nước trong bình.
b) Nếu đặt bình nước thẳng đứng sao cho phần nửa hình cầu ở trên thì chiều cao mực nước trong bình là bao nhiêu?
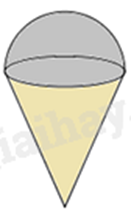
Một que kem ốc quế gồm hai phần: phần kem có dạng hình cầu, phần ốc quế có dạng hình nón. Biết bán kính hình cầu và bán kính hình nón bằng nhau và bằng 2,5 cm; chiều cao của hình nón gấp 3 lần bán kính hình cầu. Tính thể tích của que kem? (Lấy \(\pi = 3,14\) và làm tròn kết quả đến hàng đơn vị).
-
A.
\(55\left( {c{m^3}} \right)\)
-
B.
\(82\left( {c{m^3}} \right)\)
-
C.
\(28\left( {c{m^3}} \right)\)
-
D.
\(85\left( {c{m^3}} \right)\)
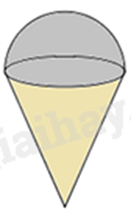
Một cơ sở sản xuất kem chuẩn bị làm 500 chiếc kem theo đơn đặt hàng. Cốc đựng kem có bề dày không đáng kể dạng hình nón chiều cao 10 cm, đường kính miệng cốc bằng 6 cm. Kem được đổ đầy vào cốc và dư ra phía ngoài một lượng có dạng nửa hình cầu có bán kính bằng bán kính miệng cốc (xem hình). Tính lượng kem cần dùng?
-
A.
\(14000\pi \;\left( {c{m^3}} \right)\).
-
B.
\(34000\pi \;\left( {c{m^3}} \right)\).
-
C.
\(24000\pi \;\left( {c{m^3}} \right)\).
-
D.
\(44000\pi \;\left( {c{m^3}} \right)\).
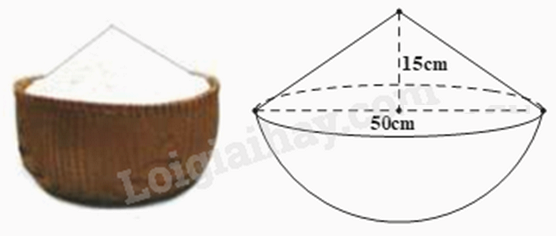
Cho hình dưới đây là một thúng gạo vun đầy. Thúng có dạng nửa hình cầu với đường kính \(50\,cm\), phần gạo vun lên có dạng hình nón cao \(15\,cm\). Hỏi thể tích phần gạo trong thúng là bao nhiêu \(d{m^3}\)? (Lấy \(\pi \approx 3,14\) và kết quả làm tròn đến hàng đơn vị)
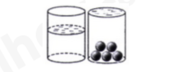
a) Tính thể tích nước tinh khiết được chứa trong ly.
b) Người ta thả vào ly nước 5 viên bi hình cầu giống hệt nhau, có cùng thể tích, đồng chất và ngập hoàn toàn trong nước, làm nước trong ly dâng lên đúng bằng miệng ly, không tràn ra ngoài. Hỏi thể tích của mỗi viên bi là bao nhiêu xăng-ti-mét khối? (Giả sử độ dày của ly là không đáng kể)
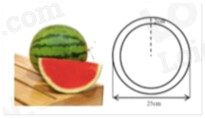
a) Coi phần ruột màu đỏ cũng có dạng hình cầu có cùng tâm với quả dưa hấu. Tính thể tích phần ruột quả dưa hấu.
(Kết quả làm tròn đến hàng phần trăm của \(c{m^3}\))
b) Người ta ép phần ruột màu đỏ của quả dưa hấu trên thì thể tích nước ép thu được bằng \(80\% \) thể tích phần ruột. Nước ép dưa hấu sẽ được đựng trong các ly thuỷ tinh giống nhau, phần lòng trong dạng hình trụ có chiều cao $10cm$ và đường kính đáy lòng trong là $5cm.$ Mỗi ly chỉ chứa \(70\% \) thể tích. Hỏi để đựng nước ép của quả dưa hấu nói trên thì cần ít nhất bao nhiêu cái ly?
Biết công thức thể tích hình trụ là \(V = p{R^2}h\) (R là bán hính đáy; h là chiều cao); công thức tính thể tích hình cầu là \(V = \frac{4}{3}p{R^3}.\)
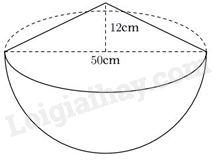
a) Tính thể tích phần gạo trong thùng.
b) Nhà bạn An dùng lon sữa bò dạng hình trụ với bán kính đáy là \(5cm\), chiều cao \(14cm\) dùng để đong gạo mỗi ngày. Biết rằng mỗi ngày nhà An ăn 4 lon gạo và mỗi lần đong thì lượng gạo chiếm \(90\% \) thể tích của lon. Hỏi cần ít nhất bao nhiêu ngày để nhà An có thể ăn hết số gạo trong thùng?
a) Tính thể tích hộp kem.
b) Hộp kem chứa kem sẽ được chia vào các bánh ốc quế hình nón có chiều cao \(12{\mkern 1mu} {\rm{cm}}\) và đường kính \(6{\mkern 1mu} {\rm{cm}}\), có hình bán cầu trên đỉnh như hình vẽ. Hãy tìm số que kem có thể chia được.


Quán nhà bạn An dùng 1 chiếc nồi hình trụ có bán kính đáy nồi là 25cm, chiều cao nồi là 0,8m để nấu nước lèo phở bò. Sau khi vớt xương và các gia vị thì lượng nước lèo trong nồi chiếm 90% thể tích nồi.
a) Tính thể tích nồi nước lèo nhà bạn An nấu, biết lượng nước lèo trong nồi chiếm 90% thể tích nồi. (ghi kết quả đến \(c{m^3}\))
b) Để bán phở bò, mỗi lần bán 1 tô phở, mẹ bạn An dùng cái vá có dạng nửa hình cầu bán kính 6,5cm và múc đúng 1 vá cho mỗi tô. Hỏi sau khi bán hết phở bò thì quán nhà bạn An thu được bao nhiêu tiền? Biết giá 1 tô phở bò là 35 000 đồng.
(biết công thức tính thể tích hình trụ là \(V = 3,14.{r^2}.h\) và công thức tính thể tích hình cầu là \(V = \frac{4}{3}.3,14.{R^3}\))
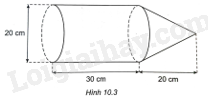
Bác Khôi làm một dụng cụ bằng tôn gồm một phần có dạng hình trụ và một phần có dạng hình nón với các kích thước như Hình 10.3. Tính thể tích của dụng cụ này (coi mép hàn không đáng kể và làm tròn kết quả đến hàng đơn vị của \(c{m^3}\)).
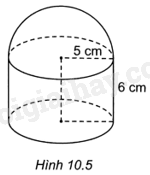
Một hộp đựng mĩ phẩm được thiết kế thân hộp có dạng hình trụ, nắp hộp có dạng nửa hình cầu với kích thước như Hình 10.5. Nếu sơn bên ngoài vỏ hộp (không sơn đáy) thì diện tích cần sơn là bao nhiêu?
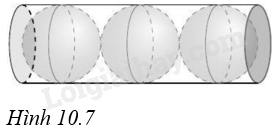
Một hộp đựng bóng bàn có dạng hình trụ chứa vừa khít 3 quả bóng bàn có cùng bán kính R xếp theo chiều ngang (H.10.7). Gọi \({S_1}\) là tổng diện tích của ba quả bóng bàn, \({S_2}\) là diện tích xung quanh của vỏ hộp hình trụ. Tính tỉ số \(\frac{{{S_1}}}{{{S_2}}}\).
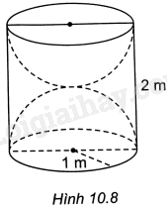
Một khối gỗ hình trụ tròn xoay có bán kính đáy bằng 1m, chiều cao bằng 2m. Người ta khoét từ hai đầu khối gỗ hai nửa hình cầu mà đường tròn đáy của khối gỗ là đường tròn lớn của mỗi nửa khối cầu (H.10.8). Tính tỉ số thể tích phần còn lại của khối gỗ và cả khối gỗ ban đầu.
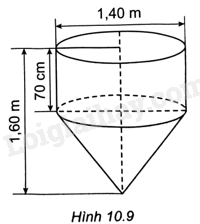
Một dụng gồm một phần có dạng hình trụ và một phần có dạng hình nón với kích thước như Hình 10.9.
a) Tính thể tích của dụng cụ này.
b) Tính diện tích mặt ngoài của dụng cụ (không tính nắp đậy, kết quả làm tròn đến hàng phần mười của \({m^2}\)).
Một vật thể bằng kim loại gồm có một hình nón và một nửa hình cầu có chung đáy. Hình nón có chiều cao 4cm và đường kính đáy là 6cm.
a) Hãy tìm thể tích và tổng diện tích bề mặt của vật thể.
b) Vật thể được nấu chảy và đúc lại thành một hình trụ có chiều cao 4cm. Tìm bán kính đáy của hình trụ đó (làm tròn kết quả đến hàng phần trăm của cm).
c) Nếu sơn 1 000 hình trụ như ở câu b và mỗi hộp sơn có thể dùng để sơn một diện tích \(5{m^2}\) thì cần bao nhiêu hộp sơn (làm tròn kết quả đến hàng đơn vị của \(c{m^2}\)).
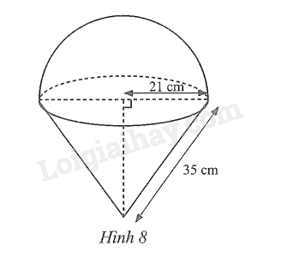
Một vật thể đặc gồm một phần dạng nửa hình cầu và một phần dạng hình nón với các số đo như Hình 8. Tính thể tích và diện tích bề mặt của vật thể này (kết quả làm tròn đến hàng đơn vị của xăngtimét khối, xăngtimét vuông).







Danh sách bình luận