Khi cắt một hình cầu bởi một mặt phẳng đi qua tâm của hình cầu đó được một hình tròn có diện tích \(25\pi \;c{m^2}\). Tính bán kính của hình cầu.
+ Chỉ ra bán kính của hình tròn là bán kính của hình cầu.
+ Sử dụng công thức tính diện tích hình tròn: \(S = \pi {R^2}\) để tính R.
Do cắt hình cầu bởi một mặt phẳng đi qua tâm của hình cầu nên bán kính của hình tròn bằng bán kính của hình cầu.
Gọi R là bán kính của hình cầu.
Khi đó ta có: \(\pi {R^2} = 25\pi \), suy ra \({R^2} = 25\) nên \(R = 5cm\).

Các bài tập cùng chuyên đề
Sọ dừa được xem là có dạng hình cầu. Người ta cắt sọ dừa khô để làm gáo dừa (H.10.22a). Em thấy miệng gáo có dạng hình gì?

Khi cắt đôi một quả cam có dạng hình cầu (H.10.22b), em thấy mặt cắt có dạng hình gì?

Quan sát Hình 5 và cho biết mặt cắt quả cam có dạng hình gì.

Mặt trên của bình gốm (Hình 8) được xem là phần chung của mặt phẳng và mặt cầu. Mặt trên của bình gốm dạng gì?

Cắt một hình cầu có bán kính 5 cm bằng một mặt phẳng đi qua tâm ta sẽ được hai nửa hình cầu. Nam cầu sơn tất cả các mặt của một nửa hình cầu này (Hình 18). Hỏi diện tích Nam cần sơn là bao nhiêu (kết quả làm tròn đến hàng đơn vị)?

a) Chuẩn bị một quả cam có dạng hình cầu. Dùng dao để cắt nó thành 2 phần. Phần mặt cắt của quả cam như ở hình 32 có dạng hình gì?
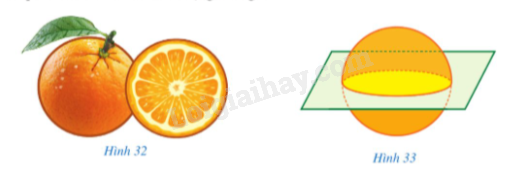
b) Quan sát hình 33 và cho biết một mặt phẳng cắt một hình cầu sẽ tạo ra hình gì?
Quan sát Hình 9.35, hãy cho biết khi bổ quả cam có dạng hình cầu thì mặt cắt của quả cam có dạng hình gì.

Cho hình cầu tâm I đường kính 1 dm. Khi cắt hình cầu trên bởi một mặt phẳng ta được một hình tròn có chu vi \(\frac{\pi }{2}\)dm. Mặt phẳng đó có đi qua tâm I của mặt cầu không? Vì sao?
Khi cắt mặt cầu bán kính R bởi một mặt phẳng không đi qua tâm của mặt cầu ta được
A. Một tam giác
B. Một hình vuông
C. Một hình tròn có bán kính R
D. Một hình tròn có bán kính bé hơn R.
Khi cắt hình cầu tâm \(O\) bán kính \(R\) bởi một mặt phẳng bất kỳ thì mặt cắt thu được luôn là một
-
A.
hình chữ nhật.
-
B.
hình tròn.
-
C.
đường tròn.
-
D.
hình vuông.
Trái Đất của chúng ta được xem là có dạng hình cầu, có bán kính là R. Khi đó bán kính của đường xích đạo là
-
A.
\(2R\).
-
B.
\(\frac{R}{2}\).
-
C.
\(4R\).
-
D.
R.
Một trái bóng nổi trên mặt nước yên lặng (Hình 7). Đường viền của mặt nước và trái bóng có dạng hình gì?

Quan sát hình sau cho biết phần chung giữa mặt phẳng và hình cầu là hình gì?
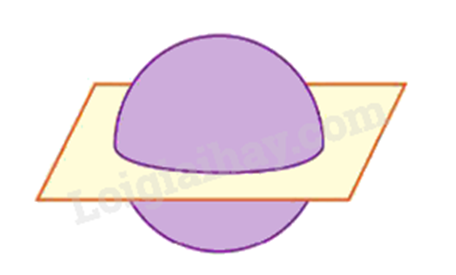
-
A.
Hình vuông.
-
B.
Hình chữ nhật.
-
C.
Hình tròn.
-
D.
Hình thang.






