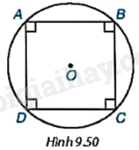
Cho hình vuông ABCD nội tiếp đường tròn (O) như Hình 9.50.
a) Phép quay thuận chiều \({90^o}\) tâm O biến các điểm A, B, C, D thành những điểm nào? Phép quay này có giữ nguyên hình vuông ABCD không?
b) Hãy liệt kê thêm ba phép quay khác với tâm O theo chiều kim đồng hồ giữ nguyên hình vuông ABCD.
+ Phép quay thuận chiều \({\alpha ^o}\left( {{0^o} < {\alpha ^o} < {{360}^o}} \right)\) tâm O giữ nguyên điểm O, biến điểm A khác điểm O thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm A tạo nên cung AB có số đo \({\alpha ^o}\).
+ Một phép quay được gọi là giữ nguyên một đa giác đều H nếu phép quay đó biến mỗi điểm của H thành một điểm của H.
a) Phép quay thuận chiều \({90^o}\) tâm O biến các điểm A, B, C, D thành những điểm tương ứng B, C, D, A.
b) Ba phép quay khác với tâm O theo chiều kim đồng hồ giữ nguyên hình vuông ABCD là phép quay theo chiều \({\alpha ^o}\) tâm O với \({\alpha ^o}\) lần lượt nhận các giá trị \({180^o},{270^o},{360^o}\).

Các bài tập cùng chuyên đề
Hãy liệt kê 6 phép quay giữ nguyên một lục giác đều nội tiếp một đường tròn (O).
Liệt kê năm phép quay giữ nguyên một ngũ giác đều nội tiếp một đường tròn tâm O.
Một vòng quay may mắn có dạng hình đa giác đều 10 cạnh (Hình 9). Tìm các phép quay biến đa giác này thành chính nó.

Đường viền ngoài của chiếc đồng hồ trong Hình 13 được làm theo hình đa giác đều nào? Tìm phép quay biến đa giác này thành chính nó.

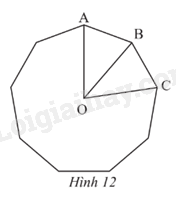
Cho đa giác đều 9 cạnh có tâm O và AB, BC là hai cạnh đa giác (Hình 12).
a) Tìm số đo các góc \(\widehat {AOB}\), \(\widehat {ABO}\), \(\widehat {ABC}\).
b) Tìm các phép quay biến đa giác thành chính nó.
Vòng trong của mái giếng trời hình hoa sen của nhà ga Bến Thành (Thành phố Hồ Chí Minh) có dạng đa giác đều 12 cạnh (Hình 14).
Hãy chỉ ra các phép quay biến đa giác đều thành chính nó.

Cắt một miếng bìa có dạng hình lục giác đều A1A2A3A4 A5A6 với tâm O và ghim miếng bìa đó lên bảng tại điểm O (Hình 27).
a) Quay miếng bìa đó theo phép quay thuận chiều \(60^\circ \) tâm O (Hình 28a). Hãy cho biết qua phép quay trên:
- Các điểm A1, A2, A3, A4, A5, A6 lần lượt quay đến vị trí mới là các điểm nào.
- Hình lục giác đều A1A2A3A4A5A6 sau khi quay đến một hình mới có trùng với chính nó hay không?
b) Quay miếng bìa đó theo phép quay ngược chiều \(60^\circ \) tâm O (Hình 28b). Hãy cho biết qua phép quay trên:
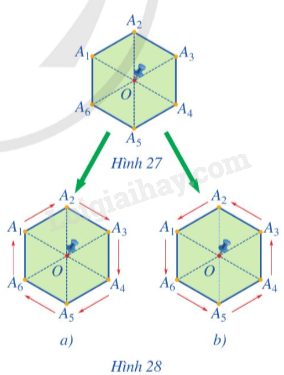
- Các điểm A1, A2, A3, A4, A5, A6 lần lượt quay đến vị trí mới là các điểm nào.
- Hình lục giác đều A1A2A3A4A5A6 sau khi quay đến một hình mới có trùng với chính nó hay không?
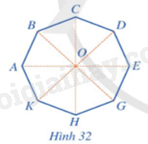
Cho hình đa giác đều có 8 cạnh ABCDEGHK với tâm O (Hình 32). Chỉ ra các phép quay tâm O giữ nguyên hình đa giác đều đã cho.
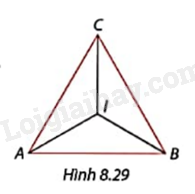
Trong Hình 8.29, tam giác ABC đều và \(\widehat {AIB} = \widehat {BIC} = \widehat {AIC} = {120^o}\). Tìm hai phép quay tâm I giữ nguyên tam giác đều ABC.
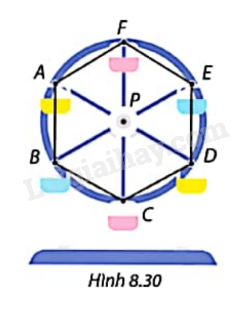
Một vòng quay có 6 cabin tại vị trí các đỉnh của một lục giác đều ABCDEF như Hình 8.30. Vòng quay này quay theo chiều quay kim đồng hồ. Tìm một phép quay tâm P (P là vị trí trục của vòng quay) để:
a) Cabin ở vị trí A di chuyển đến vị trí E. Khi đó cabin ở vị trí E di chuyển đến vị trí nào?
b) Cabin ở vị trí A di chuyển đến vị trí D. Tìm ảnh của các đỉnh còn lại của lục giác đều ABCDEF qua phép quay này và rút nhận xét.
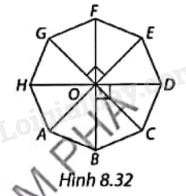
Cho bát giác đều ABCDEFGH như Hình 8.32. Biết điểm O cách đều các đỉnh của bát giác đều.
a) Tìm ảnh của tam giác OAB qua phép quay ngược chiều 180o tâm O.
b) Tìm ảnh của bát giác đều qua phép quay thuận chiều 90o tâm O và nhận xét.
c) Tìm ba phép quay tâm O giữ nguyên bát giác đều này.
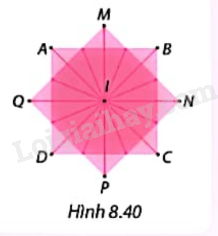
Trong Hình 8.40, phần chung của hai hình vuông ABCD và MNPQ là một hình bát giác đều.
a) Các phép quay nào giữ nguyên cả hai hình vuông ABCD và MNPQ?
b) Tìm hai phép quay giữ nguyên hình bát giác đều.
Cho hình vuông ABCD tâm O. Phép quay giữ nguyên hình vuông ABCD là
A. Phép quay thuận chiều 45o tâm O.
B. Phép quay thuận chiều 270o tâm O.
C. Phép quay ngược chiều 90o tâm A.
D. Phép quay ngược chiều 180o tâm A.
Cho hình đa giác đều có 12 cạnh \({A_1}{A_2}{A_3}...{A_{11}}{A_{12}}\), với tâm O. Tìm phát biểu sai trong các phát biểu đúng:
-
A.
Các phép quay thuận chiều tâm O, với lần lượt nhận các giá trị \(30^\circ ,{{ }}60^\circ ;{{ }}90^\circ ;{{ }}...;{{ }}330^\circ ,{{ }}360^\circ \) giữ nguyên hình đa giác đều \({A_1}{A_2}{A_3}...{A_{11}}{A_{12}}\).
-
B.
Các phép quay thuận chiều tâm O, với lần lượt nhận các giá trị \(45^\circ ,{{ }}90^\circ ;{{ }}135^\circ ;{{ }}...;{{ 315}}^\circ ,{{ }}360^\circ \) giữ nguyên hình đa giác đều \({A_1}{A_2}{A_3}...{A_{11}}{A_{12}}\).
-
C.
Các phép quay ngược chiều tâm O, với lần lượt nhận các giá trị \(20^\circ ;{{ }}40^\circ ;{{ }}...;{{ }}340^\circ ;{{ }}360^\circ \) giữ nguyên hình đa giác đều \({A_1}{A_2}{A_3}...{A_{11}}{A_{12}}\).
-
D.
Các phép quay ngược chiều tâm O, với lần lượt nhận các giá trị \(15^\circ ,{{ }}30^\circ ;{{ }}45^\circ ;{{ }}...;{{ }}345^\circ ,{{ }}360^\circ \) giữ nguyên hình đa giác đều \({A_1}{A_2}{A_3}...{A_{11}}{A_{12}}\).
Chọn đáp án đúng: 5 phép quay thuận chiều kim đồng hồ tâm \(O\) giữ nguyên ngũ giác đều nội tiếp đường tròn tâm \(O\) là:
-
A.
\({72^o}\,\,;\,\,{144^o}\,\,;\,\,{216^o}\,\,;\,\,{288^o}\,\,;\,\,{360^o}\)
-
B.
\({60^o}\,\,;\,\,{120^o}\,\,;\,\,{180^{o\,\,}};\,\,{240^o}\,\,;\,\,{300^o}\)
-
C.
\({50^o}\,\,;\,\,{100^o}\,\,;\,\,{144^o}\,\,;\,\,{288^o}\,\,;\,\,{360^o}\)
-
D.
\({72^o}\,\,;\,\,{144^{o\,\,}};\,\,{210^o}\,\,;\,\,{240^o}\,\,;\,\,{300^o}\)
Cho hình vuông \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) như hình vẽ. Trong các phép quay thuận chiều \({\alpha ^o}\) tâm \(O\) phép quay giữ nguyên hình vuông khi \(\alpha \) bằng:

-
A.
\({180^o}\)
-
B.
\({60^o}\)
-
C.
\({75^o}\)
-
D.
\({120^o}\)
Phép quay với O là tâm biến tam giác đều thành chính nó là phép quay thuận chiều một góc:
-
A.
\({90^o}\)
-
B.
\({100^o}\)
-
C.
\({110^o}\)
-
D.
\({120^o}\)
Một vòng quay may mắn có dạng hình đa giác đều 10 cạnh. Phép quay biến đa giác này thành chính nó là:
-
A.
\(75^\circ ;108^\circ ;180^\circ \).
-
B.
\(36^\circ ;144^\circ ;324^\circ \).
-
C.
\(210^\circ ;360^\circ ;252^\circ \).
-
D.
\(288^\circ ;216^\circ ;75^\circ \).
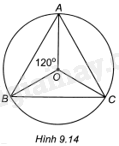
Cho tam giác đều ABC nội tiếp đường tròn (O) như Hình 9.14. Hãy cho biết các phép quay thuận chiều lần lượt \({120^o};{240^o};{360^o}\) với tâm O biến các đỉnh A, B, C thành những điểm nào.
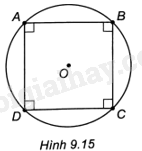
Cho hình vuông ABCD nội tiếp đường tròn (O) như Hình 9.15. Hãy cho biết các phép quay ngược chiều \({90^o};{180^o};{270^o};{360^o}\) với tâm O biến các đỉnh A, B, C, D thành những điểm nào.
Cho lục giác đều ABCDEF nội tiếp đường tròn tâm O.
a) Chứng tỏ ACE là tam giác đều.
b) Liệt kê ba phép quay giữ nguyên tam giác đều ACE.
c) Liệt kê sáu phép quay giữ nguyên lục giác đều ABCDEF.
Một phép quay thuận chiều \({120^o}\) tâm O biến điểm A thành điểm B, biến điểm B thành điểm C. Chứng tỏ rằng tam giác ABC là tam giác đều nội tiếp một đường tròn tâm O.
Cho O là trung điểm của đoạn thẳng AB.
a) Tìm một phép quay biến điểm A thành điểm B và biến điểm B thành điểm A.
b) Phép quay thuận chiều \({90^o}\) tâm O biến A thành C và biến B thành D. Chứng tỏ rằng ACBD là một hình vuông.
Cho đa giác đều H có 12 cạnh, nội tiếp một đường tròn (O). Kẻ các đoạn thẳng nối O với các đỉnh của H và thu được 12 góc nhọn tại đỉnh O (không chồng lên nhau).
a) Chứng tỏ rằng mỗi góc nhọn này có số đo bằng \({30^o}\).
b) Hãy chỉ ra 12 phép quay giữ nguyên H.
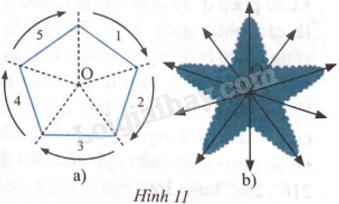
Dựa trên gợi ý của hình ngũ giác đều (Hình 11a), tìm phép quay biến hình con sao biển thành chính nó (Hình 11b).
Cho hình vuông ABCD có O là giao điểm của hai đường chéo. Phép quay tâm O biến hình vuông ABCD thành chính nó có góc quay là
A. 45o
B. 90o
C. 135o
D. 210o
Cho hình vuông ABCD với tâm O. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AD, DC, CB, BA (Hình 15).
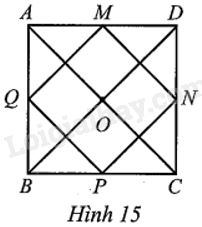
a) Chứng minh tứ giác MNPQ là hình vuông.
b) Phép quay ngược chiều 90° tâm O biến các điểm O, D, N tương ứng thành các điểm nào?
c) Chỉ ra các phép quay tâm O giữ nguyên hình vuông MNPQ.
Trên mặt phẳng tọa độ Oxy, cho hình vuông ABCD với A(1; 1), B(–1; 1), C(–1; –1), D(1; –1). Phép quay ngược chiều 45° tâm O biến các điểm A, B, C, D lần lượt thành các điểm A’, B’, C’, D’. Tính diện tích tứ giác A’B’C’D’.
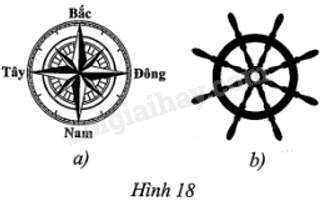
Khi quan sát la bàn (Hình 18a), bác An thấy con tàu mà bác điều khiển đang đi thẳng và di chuyển về hướng Bắc. Hỏi bác phải thực hiện phép quay nào trên bánh lái (Hình 18b) để con tàu rẽ sang:
a) Hướng Tây?
b) Hướng Đông?
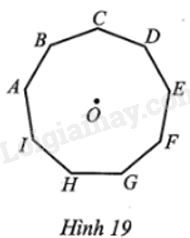
Cho hình đa giác đều có 9 cạnh ABCDEFGHI với tâm O (Hình 19). Tìm phát biểu sai, phát biểu đúng trong các phát biểu sau:
a) Các phép quay thuận chiều α° tâm O, với α° lần lượt nhận các giá trị 40°; 80°; …; 320°; 360° giữ nguyên hình đa giác đều ABCDEFGHI .
b) Phép quay ngược chiều 80° tâm O biến các điểm A, B, C, D, E lần lượt thành các điểm H, I, E, B, C.
c) Phép quay ngược chiều 120° tâm O biến các điểm A, B, C, D, E lần lượt thành các điểm G, H, I, A, C.







Danh sách bình luận