Cho bảng tần số ghép nhóm sau về thời gian gọi (phút) của một số cuộc gọi điện thoại

Vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng cho bảng thống kê trên.
+ Lập bảng tần số tương đối ghép nhóm cho bảng số liệu.
+ Cách vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng:
Bước 1: Chọn giá trị \({x_i} = \frac{{{a_i} + {a_{i + 1}}}}{2}\) đại diện cho các nhóm số liệu \(\left[ {{a_i};{a_{i + 1}}} \right)\) với \(i = 1,2,3,..,k\).
Bước 2: Vẽ trục ngang để biểu diễn các giá trị đại diện cho nhóm số liệu, vẽ trục đứng thể hiện tần số tương đối.
Bước 3: Với mỗi giá trị đại diện \({x_i}\) trên trục ngang và tần số tương đối \({f_i}\) tương ứng, ta xác định một điểm \({M_i}\left( {{x_i};{f_i}} \right)\). Nối các điểm liên tiếp với nhau.
Bước 4: Ghi chú giải cho các trục, các điểm và tiêu đề của biểu đồ.
+ Tổng số cuộc gọi là: \(6 + 14 + 20 + 12 + 8 = 60\)
Tần số tương đối của các nhóm số liệu \(\left[ {0,5;2,5} \right)\), \(\left[ {2,5;4,5} \right)\), \(\left[ {4,5;6,5} \right)\), \(\left[ {6,5;8,5} \right)\), \(\left[ {8,5;10,5} \right)\) lần lượt là: \(\frac{6}{{60}} = 10\% ;\frac{{14}}{{60}} \approx 23,33\% ;\frac{{20}}{{60}} \approx 33,33\% ;\frac{{12}}{{60}} = 20\% ;\frac{8}{{60}} \approx 13,34\% \)
Ta có bảng tần số tương đối ghép nhóm:

+ Vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng:
Bước 1: Chọn giá trị đại diện cho các nhóm số liệu ta có bảng sau:

Bước 2: Vẽ các trục
Bước 3: Xác định các điểm, nối các điểm liên tiếp với nhau.

Bước 4: Ghi chú giải cho các trục, các điểm và tiêu đề của biểu đồ tần số tương đối ghép nhóm.


Các bài tập cùng chuyên đề
Cho bảng tần số tương đối ghép nhóm về thời gian từ nhà đến trường của học sinh lớp 9A như sau:

Để vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng, ta dùng giá trị nào đại diện cho nhóm số liệu \(\left[ {10;20} \right)\)?
A. 10.
B. 15.
C. 20.
D. 30.
Xét mẫu số liệu ghép nhóm ở Ví dụ 4 với bảng tần số tương đối ghép nhóm là Bảng 34.

Trên mặt phẳng hãy:
a) Xác định đầu mút trái, đầu mút phải, tần số tương đối \({f_1}\) của nhóm 1 ứng với nửa khoảng [0; 20). Từ đó xác định điểm \({M_1}({c_1};{f_1})\), trong đó \({c_1}\)là trung bình cộng hai đầu mút của nhóm 1.
b) Bằng cách tương tự, xác định các điểm \({M_2}({c_2};{f_2}),{M_3}({c_3};{f_3}),{M_4}({c_4};{f_4}),{M_5}({c_5};{f_5})\), trong đó \({c_2},{c_3},{c_4},{c_5}\)lần lượt là trung bình cộng hai đầu mút của nhóm 2, 3, 4, 5.
c) Vẽ đường gấp khúc \({M_1}{M_2}{M_3}{M_4}{M_5}\).
Vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng của bảng tần số tương đối ghép nhóm lập được ở Luyện tập 2 (về lợi nhuận của cửa hàng điện máy).
Luyện tập 2
Bảng tần số - tần số tương đối ghép nhóm

Biểu đồ đoạn thẳng dưới đây biểu diễn thời gian (đơn vị: phút) sử dụng điện thoại di động trong một ngày của một nhóm học sinh.
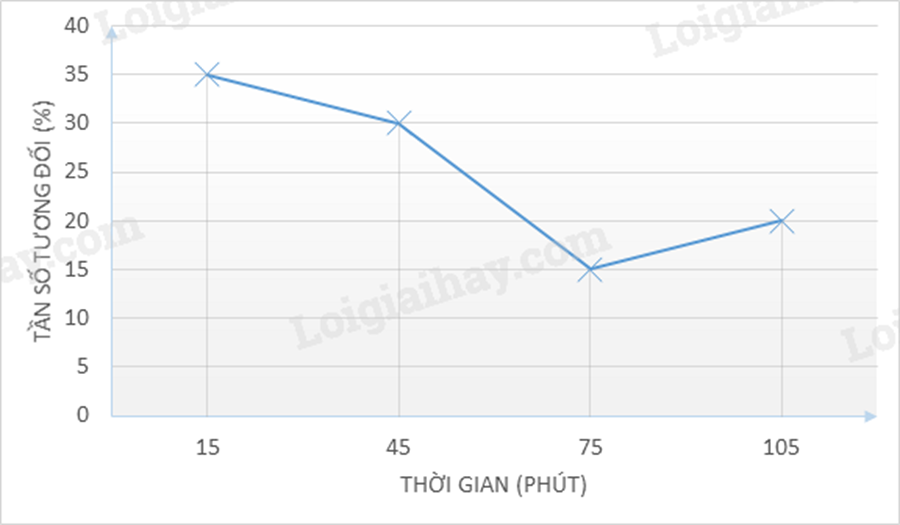
Hãy cho đâu là bảng tần số tương đối ghép nhóm của dữ liệu thống kê của biểu đồ trên.
-
A.
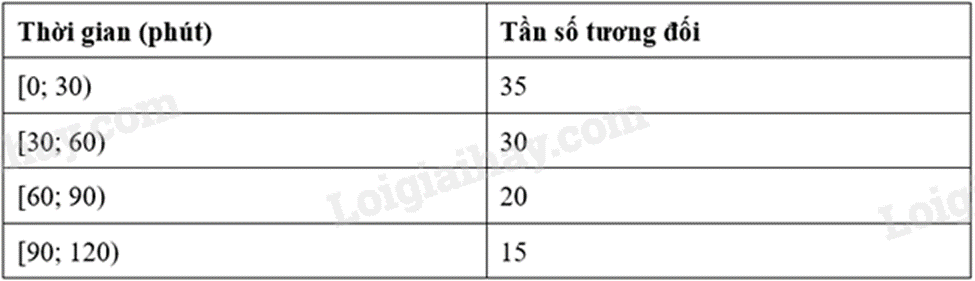
-
B.
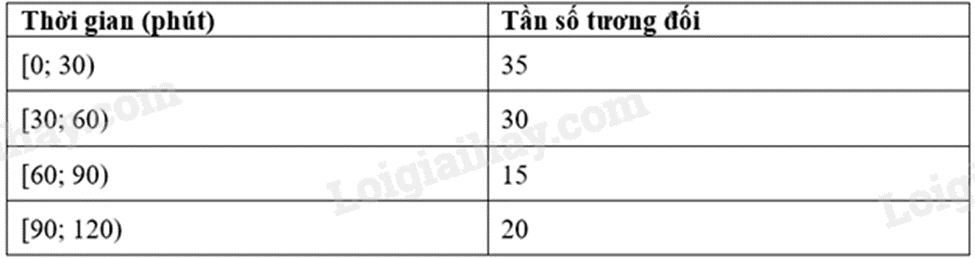
-
C.
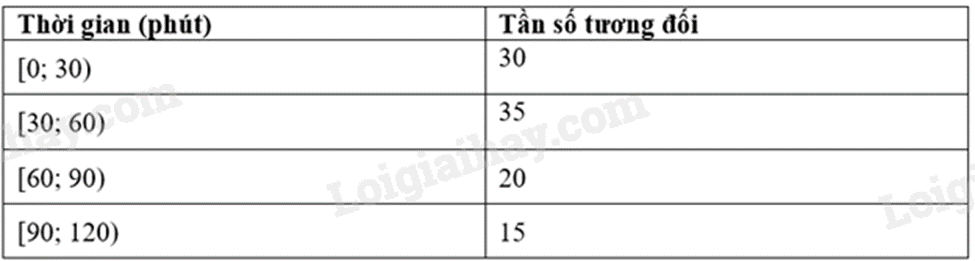
-
D.
Cho biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng sau:
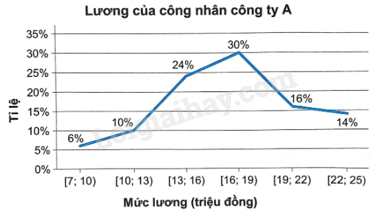
a) Đọc và giải thích thông tin về hai nhóm dữ liệu được biểu diễn trên biểu đồ.
b) Lập bảng tần số tương đối ghép nhóm cho dữ liệu được biểu diễn trên biểu đồ.
c) Biết rằng công ty A có 300 người, lập bảng tần số ghép nhóm cho lương của công nhân công ty này.
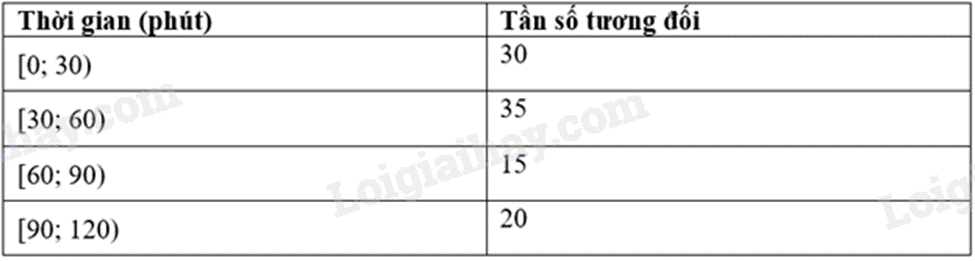
Bảng tần số tương đối ghép nhóm sau cho biết thông tin về tỉ lệ học sinh lớp 9A theo khoảng cách từ nhà đến trường:

Để vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng biểu diễn bảng thống kê trên ta chọn giá trị nào làm giá trị đại diện cho nhóm [2; 3)?
A. 0,5.
B. 1,5.
C. 2,5.
D. 3,5.
Độ dài một cú nhảy ba bước (đơn vị: m) của 40 học sinh lớp 9 được ghi lại ở bảng tần số ghép nhóm sau:

a) Tìm tần số tương đối của mỗi nhóm.
b) Lập bảng tần số tương đối ghép nhóm cho mẫu số liệu trên.
c) Vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng biểu diễn mẫu số liệu trên.
d) Một giáo viên thể dục muốn chọn ra 15% học sinh có thành tích nhảy ba bước tốt nhất. Hỏi giáo viên nên chọn các học sinh có độ dài bước nhảy tối thiểu là bao nhiêu mét?
Cho biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng về chiều cao của học sinh nữ lớp 9C.

Lớp 9C cần chọn ra những bạn nữ cao từ 160cm trở lên để tham gia đội tuyển thi đấu bóng chuyền. Nếu lớp 9C có 20 bạn nữ thì số bạn được tham gia đội tuyển bằng bao nhiêu.
Thời gian đi từ nhà tới trường (đơn vị: phút) của các bạn học sinh lớp 9C được biểu diễn bởi biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng như sau:
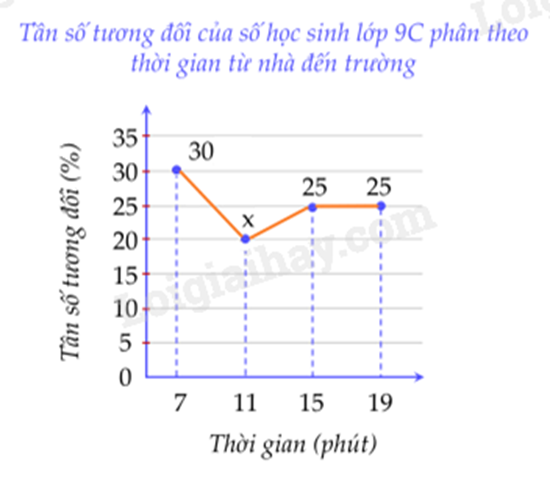
Biết lớp 9C có 40 học sinh. Số học sinh tương ứng với tần số tương đối x là:
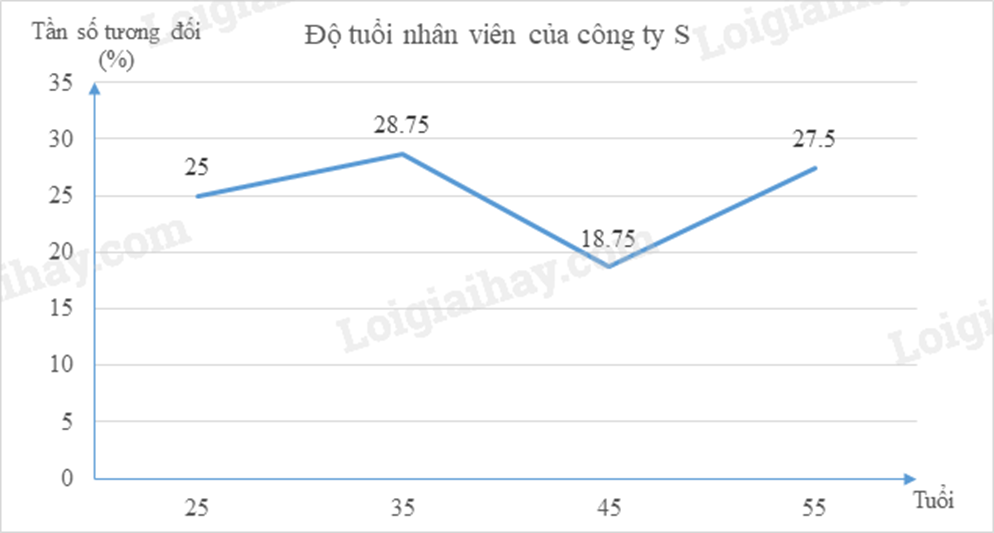
Khảo sát độ tuổi nhân viên của công ty S được chia ra làm 4 nhóm chính: từ 20 tuổi đến dưới 30 tuổi, từ 30 tuổi đến dưới 40 tuổi, từ 40 tuổi đến dưới 50 tuổi và từ 50 tuổi đến dưới 60 tuổi và kết quả được biểu diễn qua biểu đồ đoạn thẳng như hình vẽ dưới đây. Biết tổng số nhân viên có độ tuổi từ 20 đến dưới 40 tuổi là 430 người. Tính số nhân viên có độ tuổi từ 20 đến dưới 30 tuổi.
Cho bảng tần số tương đối ghép nhóm về thời gian đi từ nhà đến trường của học sinh lớp \(9A\) như sau:
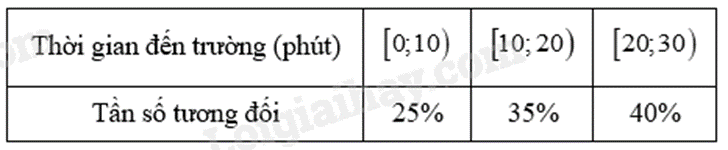
Để vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng, ta dùng giá trị nào đại diện cho nhóm số liệu \(\left[ {20;30} \right)\).
-
A.
\(5\).
-
B.
\(15\).
-
C.
\(25\).
-
D.
\(20\).







Danh sách bình luận