Giải bài toán trong tình huống mở đầu.
Tình huống mở đầu: Bác An có 40m hàng rào lưới thép, Bác muốn dùng nó để rào xung quanh một mảnh đất trống (đủ rộng) thành một mảnh vườn hình chữ nhật có diện tích \(96{m^2}\) để trồng rau. Tính chiều dài và chiều rộng của mảnh vườn đó.
+ Chiều dài và chiều rộng của mảnh vườn là nghiệm của phương trình: \({x^2} - 20x + 96 = 0\)
+ Giải phương trình ta tìm được chiều dài và chiều rộng của mảnh vườn.
Nửa chu vi của mảnh vườn là: \(40:2 = 20\left( m \right)\).
Khi đó, chiều dài và chiều rộng của mảnh vườn là nghiệm của phương trình:
\({x^2} - 20x + 96 = 0\)
Ta có: \(\Delta ' = {\left( { - 10} \right)^2} - 1.1.96 = 4\) nên phương trình có hai nghiệm \({x_1} = 10 + \sqrt 4 = 12;{x_2} = 10 - \sqrt 4 = 8\)
Do đó, chiều dài và chiều rộng của mảnh vườn lần lượt là 12m và 8m.
Chú ý khi giải: Trong hình chữ nhật, chiều dài luôn lớn hơn chiều rộng.
Các bài tập cùng chuyên đề
Cho Parabol \((P):y=\dfrac{1}{4}{{x}^{2}}\) và đường thẳng \((d):y=mx-2m+1\). Tìm m để (P) và (d) tiếp xúc nhau.
Xác định a, b’, c rồi dùng công thức nghiệm thu gọn giải các phương trình sau:
a) \(3{x^2} + 8x - 3 = 0\);
b) \({x^2} + 6\sqrt 2 x + 2 = 0\).
Giải bài toán trong tình huống mở đầu.
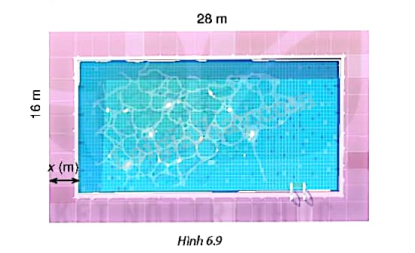
Tình huống mở đầu: Trên một mảnh đất hình chữ nhật có kích thước 28m x 16m, người ta dự định làm một bể bơi có đường đi xung quanh (H.6.9). Hỏi bề rộng của đường đi là bao nhiêu để diện tích của bể bơi là \(288{m^2}\)?
Giải các phương trình sau:
a) \(5{x^2} - 6\sqrt 5 x + 2 = 0\);
b) \(2{x^2} - 2\sqrt 6 x + 3 = 0\).
Nhu cầu của khách hàng đối với một loại áo phông tại một cửa hàng được cho bởi phương trình \(p = 100 - 0,02x\), trong đó p là giá tiền của mỗi chiếc áo (nghìn đồng) và x là số lượng áo phông bán được. Doanh thu R (nghìn đồng) khi bán được x chiếc áo phông là: \(R = xp = x\left( {100 - 0,02x} \right)\). Hỏi cần phải bán được bao nhiêu chiếc áo phông để doanh thu đạt 120 triệu đồng?
Dùng công thức nghiệm thu gọn giải các phương trình sau:
a) \(5{x^2} - 12x + 4 = 0\)
b) \(5{x^2} - 2\sqrt 5 x + 1 = 0\)
Xét phương trình \(a{x^2} + bx + c = 0(a \ne 0)\) với \(b = 2b'\).
a) Đặt \(\Delta ' = b{'^2} - ac\), chứng tỏ rằng \(\Delta = 4\Delta '.\)
b) Xét tính có nghiệm và nêu công thức nghiệm (nếu có) của phương trình trong các trường hợp: \(\Delta ' > 0;\Delta ' = 0;\Delta ' < 0.\)
Giải các phương trình:
a) \({x^2} - 6x - 5 = 0\)
b) \( - 3{x^2} + 12x - 35 = 0\)
c) \( - 25{x^2} + 30x - 9 = 0\)
Trong bài toán ở phần mở đầu, sau bao lâu thì quả bóng chạm đất?
Giả sử khi ném một quả bóng vào rổ, độ cao y (feet) của quả bóng và thời gian x (giây) liên hệ với nhau bởi công thức \(y = -5,8x^2 + 11,8x + 7\)
Khi quả bóng chạm đất, ta có thời gian x thỏa mãn phương trình \( -5,8x^2 + 11,8x + 7 = 0\)
Một nhà máy chuyên sản xuất một loại sản phẩm. Năm 2019 nhà máy sản xuất được 5000 sản phẩm. Do ảnh hưởng của dịch bệnh nên sản lượng của nhà máy trong các năm 2020 và 2021 đều giảm, cụ thể: Số lượng sản phẩm thực tế sản xuất được của năm 2020 giảm x% so với số lượng sản phẩm sản xuất được của năm 2019; Số lượng sản phẩm thực tế sản xuất được của năm 2021 giảm x% so với số lượng sản phẩm thực tế sản xuất được của năm 2020. Biết rằng số lượng sản phẩm thực tế sản xuất được của năm 2021 giảm 51% so với số lượng sản phẩm xuất được của năm 2019. Tìm x.
Cho phương trình \({x^2} + 2x + c = 0\). Điều kiện của c để phương trình có 2 nghiệm phân biệt là:
A. \(c < 1\)
B. \(c > 1\)
C. \(c \le 1\)
D. \(c \ge 1\)
Giải các phương trình:
a) \(3{x^2} - 2x - 4 = 0\)
b) \(9{x^2} - 24x + 16 = 0\)
c) \(2{x^2} + x + \sqrt 2 = 0\)
Một chiếc áo có giá niêm yết là 120 000 đồng. Để thanh lí chiếc áo, đầu tiên người ta giảm giá x% so với giá niêm yết. Do vẫn chưa bán được chiếc áo nên người ta tiếp tục giảm giá x% so với giá vừa được giảm. Sau hai đợt giảm giá, giá của chiếc áo còn 76800 đồng. Tìm x.
Một công ty sản xuất các khay có dạng hình hộp chữ nhật để trồng rau trong chung cư ở các thành phố. Biết diện tích mặt đáy của khay đó là 2 496 cm2 và chu vi mặt đáy của khay đó là 220 cm. Tìm các kích thước mặt đáy của khay đó.
Dùng công thức nghiệm thu gọn giải các phương trình sau:
a) \(3{x^2} - 6x + 5 = 0\)
b) \({y^2} + 4y - 7 = 0\)
c) \({x^2} - 4\sqrt 2 x + 7 = 0\)
Một đàn gấu mèo được thả vào một khu rừng. Sau t tháng, số lượng gấu mèo trong đàn được ước lượng bởi công thức \(P(t) = 4{t^2} + 30t + 100\)(nguồn: Chris Kirkpatrick Barbara Alldred, Crystal Chilvers, Beverly Farahani, Kristina Farentino, Angelo Lillo, lan Macpherson,John Rodger, Susanne Trew, Advanced Function, Nelson 2012, p.86). Theo công thức này, khi nào số các thể của đàn lên đến 200 con?
Một tam giác vuông có diện tích bằng 24 cm2 và có tổng độ dài hai cạnh góc vuông bằng 14. Tính chu vi tam giác vuông đó.
Cho phương trình (ẩn x): \({x^2} + 4\left( {m + 1} \right)x + 4{m^2} - 3 = 0\).
a) Tính biệt thức \(\Delta '\).
b) Tìm điều kiện của m để phương trình:
- Có hai nghiệm phân biệt;
- Có nghiệm kép;
- Vô nghiệm.
Tìm điều kiện của tham số m để phương trình \({x^2} - 2\left( {m - 2} \right)x + {m^2} - 3m + 5 = 0\) có hai nghiệm phân biệt.
A. \(m \le - 1\).
B. \(m = - 1\).
C. \(m > - 1\).
D. \(m < - 1\).
Phương trình cầu đối với một sản phẩm là \(p = 60 - 0,0004x\), trong đó p là giá tiền của mỗi sản phẩm (USD) và x là số lượng sản phẩm đã bán. Tổng doanh thu cho việc bán x sản phẩm này là:
\(R\left( x \right) = xp = x\left( {60 - 0,0004x} \right)\).
Hỏi phải bán bao nhiêu sản phẩm để doanh thu đạt được là 220 000USD?
Công thức tính huyết áp tâm thu bình thường (kí hiệu là P) của một người đàn ông ở độ tuổi A, được đo bằng mmHg, được đưa ra như sau: \(P = 0,006{A^2} - 0,02A + 120\)
(Theo Algebra and Trigonometry, Pearson Education Limited, 2014).
Tìm tuổi (làm tròn đến năm gần nhất) của người đàn ông có huyết áp bình thường là 125mmHg.
Xét phương trình \(m{x^2} - 2\left( {m - 1} \right)x + m - 3 = 0\)(1) (m là tham số).
Cho phương trình \({x^2} - 2\left( {m - 1} \right)x - 3 - m = 0\) (1) (\(m\) là tham số).
Cho phương trình \(4{x^2} + 4\left( {m + 1} \right)x - 2m - 3 = 0\) (1) (\(m\) là tham số).
Ra đa của một máy bay trực thăng theo dõi chuyển động của một ô tô trong 10 phút, phát hiện rằng tốc độ \(v(km/h)\) của ô tô thay đổi phụ thuộc vào thời gian \(t\) (phút) bởi công thức \(v(t) = 3{t^2} - 30t + 115.\) Tính giá trị của \(t\) (\(1 < t < 10)\), theo đơn vị phút và làm tròn kết quả đến hàng đơn vị) khi tốc độ ô tô bằng \(100km/h\)
Cho Parabol (P): \(y={{x}^{2}}\) và đường thẳng (d): \(y=2(m+1)x-{{m}^{2}}-9\). Tìm m để (d) tiếp xúc với (P).
Cho parabol \(\left( P \right): y = a{x^2}\left( {a \ne 0} \right)\) đi qua điểm \(A\left( { - 2;4} \right)\) và tiếp xúc với đồ thị của hàm số \(y = 2(m - 1)x - (m - 1)\).Toạ độ tiếp điểm là
Giải phương trình \(5{{x}^{4}}+2{{x}^{2}}-16=10-{{x}^{2}}\)
Với giá trị nào của m thì hệ phương trình sau có nghiệm duy nhất \(\left\{ \begin{array}{l}x + y = 8\\\dfrac{x}{y} + \dfrac{y}{x} = m\end{array} \right.\)
Cho hai phương trình \({x^2} - 13x + 2m = 0\) (1) và \({x^2} - 4x + m = 0\) (2). Xác định \(m\) để một nghiệm phương trình (1) gấp đôi \(1\) nghiệm phương trình (2).
