1. Nêu mối liên hệ giữa độ bền vững của hạt nhân và năng lượng liên kết riêng.
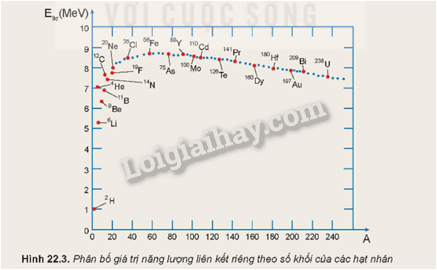
2. Giá trị năng lượng liên kết riêng Elkr của nhiều hạt nhân được biểu diễn trên đồ thị Hình 22.3. Em hãy:
a) Chỉ ra hai hạt nhân bền vững nhất, ước lượng Elkr của chúng.
b) Xác định năm hạt nhân nhẹ (A ≤ 30) và bốn hạt nhân nặng (A ≥ 160) có Elkr ≤ 8,2 MeV.
Vận dụng lí thuyết năng lượng liên kết
1. Elkr lớn cho thấy lực liên kết giữa các nuclon trong hạt nhân mạnh hơn. Lực liên kết mạnh hơn giúp hạt nhân chống lại sự phân rã. Hạt nhân có Elkr nhỏ có lực liên kết yếu hơn, dễ bị phân rã thành các hạt nhân khác để giải phóng năng lượng.
2.
a) Hai hạt nhân bền vững nhất là Fe và As
b) 5 hạt nhân nhẹ có Elkr ≤ 8,2 MeV: F, C, He, B, Be
4 hạt nhân nặng có Elkr ≤ 8,2 MeV: Hf, Au, Bi, U

Các bài tập cùng chuyên đề
Chiếc tem thư phát hành năm 1971 có in hình Rutherford và phương trình phản ứng hạt nhân được thực hiện lần đầu tiên trên thế giới vào năm 1909. Người ta đã thực hiện thí nghiệm phát hiện phản ứng hạt nhân như thế nào? Các hạt nhân có thể biến đối thành các hạt nhân khác không?

So sánh tổng số điện tích, tổng số nucleon của các hạt nhân trước và sau khi tương tác trong thí nghiệm như mô tả ở Hình 22.2.
Hãy trình bày sự khác nhau giữa phản ứng hạt nhân và phản ứng hóa học
1. Hãy viết biểu thức liên hệ giữa các số khối và biểu thức liên hệ giữa các điện tích của các hạt nhân trong phản ứng hạt nhân:
\({}_{{Z_1}}^{{A_1}}{X_1} + {}_{{Z_2}}^{{A_2}}{X_2} \to {}_{{Z_3}}^{{A_3}}{X_3} + {}_{{Z_4}}^{{A_4}}{X_4}\)
2. Khi bắn phá \({}_{92}^{235}U\) bằng neutron \({}_0^1n\) người ta thấy chúng hợp nhất thành hạt nhân X, ngay sau đó hạt nhân X phân rã thành \({}_{42}^{99}Mo\), ba hạt neutron và một hạt nhân Y.
a) Viết các phương trình phản ứng hạt nhân mô tả trong quá trình trên.
b) Sử dụng bảng hệ thống tuần hoàn hãy xác định tên gọi và kí hiệu các hạt nhân X và Y.
Vì sao để tách được các nucleon ra khỏi hạt nhân cần một năng lượng lớn?
Hãy tính độ hụt khối của hạt nhân oxygen \({}_8^{16}O\) biết khối lượng hạt nhân oxygen là m0 ≈ 15,99492 amu.
Hãy thực hiện các yêu cầu sau:
a) Tính năng lượng liên kết và năng lượng liên kết riêng của hạt nhân \({}_2^4He\)
b) Tìm hệ số chuyển đổi giữa các đơn vị amu và MeV/c2.
Một nhà máy điện hạt nhân sử dụng nguyên liệu hạt nhân là \({}^{235}U\). Biết rằng mỗi phân hạch sẽ toả năng lượng 200 MeV. Hiệu suất phát điện của nhà máy là 36%. Công suất phát điện của nhà máy là 1 400 MW.
a) Hãy tính khối lượng của nguyên liệu \({}^{235}U\) nhà máy tiêu thụ trong 1 năm.
b) Tính lượng than đá tiêu thụ để sản xuất ra năng lượng điện tương đương, biết rằng năng suất tỏa nhiệt của than đá là 30 MJ/kg.
Tính năng lượng nghỉ của một đồng xu có khối lượng 2 g đang nằm yên trên bàn theo hệ thức về mối liên hệ giữa khối lượng và năng lượng
Mặt Trời là một nguồn phát năng lượng khổng lồ với công suất rất lớn. Công suất trung bình của Mặt Trời khoảng 4.1026 W. Hãy ước tính khối lượng Mặt Trời mất đi trong mỗi giây để tạo ra được công suất nói trên.
Hãy ước lượng khối lượng riêng của hạt nhân \({}_6^{12}C\). Nhận xét.
Sử dụng hệ thức E = mc2 để xác định năng lượng của các hạt trong Bảng 15.1 theo đơn vị MeV và J.
So sánh lực đẩy tĩnh điện và lực hấp dẫn giữa hai proton đặt cách nhau 1 fm. Biết rằng điện tích của proton là 1,6.10-19 C và lực hấp dẫn giữa hai proton ở khoảng cách 1 fm là 1,87.10-34 N
Tính độ hụt khối của hai hạt nhân bất kì được cho trong Bảng 15.1.
Tính năng lượng liên kết của hai hạt nhân bất kì được cho trong Bảng 15.1.
Tính năng lượng liên kết riêng của các hạt nhân \({}_6^{12}C;{}_2^4He;{}_8^{16}O;{}_{92}^{235}U\)trong Bảng 15.1 và chỉ ra trong đó hạt nhân nào bền vững nhất và kém bền vững nhất.
Hãy thảo luận và giải thích tại sao hạt nhân \({}_1^1H\) không xuất hiện trong Hình 15.2.
a) Dựa vào Bảng 15.1, tính năng lượng liên kết và năng lượng liên kết riêng của hạt nhân \({}_{26}^{56}Fe\). Biết khối lượng của hạt nhân này là 55,934936 amu.
b) Từ kết quả câu a và Thảo luận 7, hãy so sánh mức độ bền vững của hạt nhân \({}_{26}^{56}Fe\) với các hạt nhân \({}_6^{12}C;{}_2^4He;{}_8^{16}O\) và \({}_{92}^{235}U\)
c) Kiểm tra kết quả cầu b dựa vào Hình 15.2.
Độ bền vững của hạt nhân phụ thuộc vào đại lượng vật lí nào?
A. Năng lượng liên kêt.
B. Năng lượng liên kết riêng.
C. Độ hụt khối.
D. Số khối và số neutron.
Dựa vào Bảng 15.1, tính độ hụt khối, năng lượng liên kết và năng lượng liên kết riêng của hạt nhân \({}_{82}^{206}Pb\). Biết khối lượng của hạt nhân này là 205,974466 amu.
Các proton mang điện tích dương nên đẩy nhau theo định luật Coulomb. Nguyên nhân nào khiến các proton và neutron vẫn có thể liên kết chặt chẽ với nhau trong hạt nhân?
Cho biết khối lượng của hạt nhân \({}_6^{12}C\) là 11,99993 u. Sử dụng số liệu trong bảng 1.1 trang 92, tính độ hụt khối của hạt nhân \({}_6^{12}C\).
Tính 1 MeV/c2 ra đơn vị kilôgam.
Tính năng lượng liên kết của hạt nhân \({}_6^{12}C\) ra đơn vị MeV và đơn vị J
Tính năng lượng liên kết riêng của hạt nhân \({}_6^{12}C\).
Dựa vào Hình 2.3, sắp xếp các hạt nhân sau theo thứ tự độ bền vững tăng dần:
\({}_3^6Li,{}_6^{12}C,{}_7^{14}N,{}_{10}^{20}Ne\)
Hạt nhân \({}_{26}^{56}Fe\) có năng lượng liên kết riêng bằng 8,8 MeV/nucleon là một trong những hạt nhân bền vững nhất trong tự nhiên. Tính độ hụt khối của hạt nhân này.
Ta có thể áp dụng hệ thức Einstein (2.2) để tính năng lượng tỏả ra của phản ứng phân hạch hạt nhân \({}_{92}^{235}U\) trong Hình 2.4. Trước phản ứng, tổng khối lượng các hạt là
mtrước = mn + mU
Sau phản ứng, tổng khối lượng các hạt là
msau = mKr + mBa + 3mn
Thông qua phản ứng, khối lượng của hệ đã giảm đi một lượng là:
mtrước - msau
Như vậy, phản ứng đã tỏả ra một năng lượng là
Etỏa = (mtrước - msau)c2
Cho biết khối lượng nguyên tử của các hạt trong phản ứng phân hạch Hình 2.4 như trong bảng dưới đây:
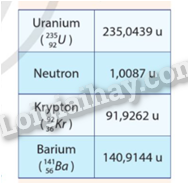
Tính năng lượng toả ra của phản ứng đó ra đơn vị MeV.
Năng lượng tỏả ra khi 1,000 kg \({}_{92}^{235}U\) bị phân hạch hoàn toàn theo phản ứng trong Hình 2.4 tương đương với năng lượng toả ra khi đốt cháy bao nhiêu tấn than đá? Cho biết: khối lượng mol nguyên tử của uranium là 235,0439 g/mol; số Avogadro NA = 6,02.1023 nguyên tử/mol.
Mỗi kg than đá khi đốt cháy hoàn toàn toả ra 27.106 J năng lượng nhiệt.
Arktika là tàu phá băng chạy bằng năng lượng hạt nhân của Nga. Với chiều dài 173 m, cao 15 m, tàu được trang bị hai lò phản ứng hạt nhân, mỗi lò có công suất 175 MW, giúp tàu phá lớp băng dày đến 3 m.
Nếu lò phản ứng này sử dụng năng lượng từ sự phân hạch của \({}_{92}^{235}U\), mỗi phân hạch sinh ra trung bình 203 MeV; tính khối lượng \({}_{92}^{235}U\) mà lò phản ứng tiêu thụ trong 1 ngày. Cho số Avogadro NA = 6,02.1023 nguyên tử/mol và khối lượng mol nguyên tử của \({}_{92}^{235}U\) là 235 g/mol.








Danh sách bình luận