Một tấm bìa tạo bởi năm đường tròn đồng tâm lần lượt có bán kính là 5 cm, 10 cm, 15 cm, 20 cm và 30 cm (H.5.17). Giả thiết rằng người ném phi tiêu một cách ngẫu nhiên và luôn trúng bia. Tính xác suất ném trúng vòng 8 (hình vành khuyên nằm giữa đường tròn thứ hai và thứ ba), biết rằng xác xuất cần tìm bằng tỉ số giữa diện tích của hình vành khuyên tương ứng với diện tích của hình tròn lớn nhất.
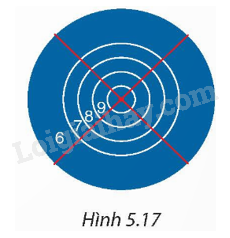
- Tính diện tích của vòng 8, diện tích của hình tròn lớn nhất.
- Xác xuất ném trúng vòng 8 = Diện tích vòng 8 : Diện tích hình tròn lớn nhất.
Diện tích của vòng 8 là: \(\pi \left( {{{15}^2} - {{10}^2}} \right) = 125\pi \,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Diện tích hình tròn lớn nhất là: \(\pi {.30^2} = 900\pi \,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\)
Xác suất ném trúng vòng 8 là: \(\frac{{125\pi }}{{900\pi }} = \frac{5}{{36}}\)
Các bài tập cùng chuyên đề
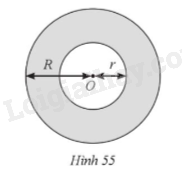
Thiết lập công thức tính diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là R và r (R > r).
Tính diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 6 cm và 4 cm.
Một chiếc quạt giấy khi xòe ra có dạng nửa hình tròn bán kính 2,2 dm như hình 5.19. Tính diện tích phần giấy của chiếc quạt, biết rằng khi gấp lại, phần giấy có chiều dài khoảng 1,6 dm (làm tròn kết quả đến hàng phần trăm của dm2).
a) Vẽ đường tròn (C) tâm O bán kính r = 5 cm và đường tròn (C’) tâm O bán kính R = 8 cm.
b) Tính diện tích S của (C) và diện tích S’ của (C’).
c) Hãy cho biết hiệu số (S’ – S) biểu diễn diện tích của phần nào trên Hình 9.
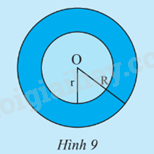
Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 10 cm) và (O; 20 cm) (kết quả làm tròn đến hàng phần trăm)
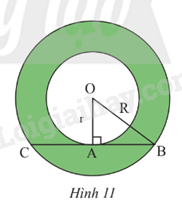
Cho hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) với R > r. Trên đường tròn (O; R) lấy hai điểm B, C sao cho BC vừa là dây cung của (O; R), vừa là tiếp tuyến của đường tròn (O; r) tại A (Hình 11)
a) Tính độ dài đoạn thẳng BC theo r và R.
b) Cho BC = \(a\sqrt 3 \). Tính diện tích hình khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) theo a.
Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 9 cm) và (O; 12 cm)
Hình vành khuyên giới hạn bởi hai đường tròn (O; 2 cm) và (O; 4 cm) có diện tích bằng
A. \(12c{m^2}\)
B. \(24c{m^2}\)
C. \(4\pi c{m^2}\)
D. \(12\pi c{m^2}\)
a) Hình 80 mô tả một phần bản vẽ của chi tiết máy. Hình đó giới hạn bởi mấy đường tròn cùng tâm?
b) Hãy vẽ một hình tương tự Hình 80 bằng cách vẽ các đường tròn \(\left( {O;2cm} \right)\) và \(\left( {O;3cm} \right)\). Tính hiệu diện tích của hai hình tròn đó.
Tính diện tích của hình vành khuyên, biết hình vành khuyên đó giới hạn bởi hai đường tròn cùng tâm và có bán kính lần lượt là 2,5cm; 2cm.
Hình 87 mô tả mặt cắt của một chiếc đèn led có dạng hai hình vành khuyên màu trắng với bán kính các đường tròn lần lượt là 15cm, 18cm, 21cm, 24cm. Tính diện tích hình vành khuyên đó.
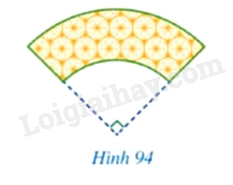
Hình 88 mô tả mặt cắt của một khung gỗ có dạng ghép của năm hình: hai nửa đường tròn đường kính 2cm; hai hình chữ nhật kích thước \(2cm \times 8cm\); một phần tư hình vành khuyên giới hạn bởi hai đường tròn cùng tâm có bán kính lần lượt là 4cm và 6cm. Tính diện tích của mặt cắt của khung gỗ đó.
Mặt đĩa CD ở Hình 93 có dạng hình vành khuyên giới hạn bởi hai đường tròn có bán kính lần lượt là 1,5cm và 6cm. Hình vành khuyên đó có diện tích bằng băng nhiêu centimét vuông (làm tròn kết quả đến hàng phần mười)?
Hình 94 mô tả mảnh vải có dạng một phần tư hình vành khuyên, trong đó hình vành khuyên giới hạn bởi hai đường tròn cùng tâm và có các bán kính lần lượt là 3dm và 5dm. Diện tích của mảnh vải đó bằng bao nhiêu decimét vuông (làm tròn kết quả đến hàng phần mười)?
Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn đồng tâm có bán kính lần lượt là 5cm và 3cm.
Trong Hình 5.57, bia bắn cung có dạng hình tròn bán kính 20cm. Bia được chia thành năm phần bởi bốn đường tròn có bán kính lần lượt 4cm, 8cm, 12cm, 16cm. Mỗi phần được sơn một màu khác nhau. Tính diện tích mỗi phần.
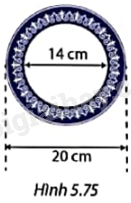
Tính chu vi đĩa sứ và diện tích phần viền tráng men xanh của đĩa sứ trong Hình 5.75.
Diện tích của hình vành khuyên giới hạn bởi hai đường tròn tâm O là \(240\pi \;c{m^2}\). Nếu đường tròn nhỏ có bán kính 17cm thì đường tròn lớn có bán kính là
A. 21cm.
B. 22cm.
C. 23cm.
D. 24cm.
Diện tích hình vành khuyên giới hạn bởi hai đường tròn \(\left( {O;r} \right)\) và \(\left( {O;R} \right)\) (với \(R > r\)) là:
Tính diện tích hình vành khuyên khi \({R_1} = 12cm,{R_2} = 7cm\).
Vòng đệm là một trong những chi tiết lót không thể thiếu giữa đai ốc và các thiết bị ghép nối trong các máy móc công nghiệp. Vòng đệm có tác dụng phân bố đều lực ép lên đai ốc, làm tăng độ chặt giữa các mối ghép. Một vòng đệm có thiết kế như hình vẽ bên, với A là tâm của hai đường tròn bán kính AD và AC. Biết D là trung điểm của AC và AD = 5cm. Tính diện tích phần tô đậm, kết quả làm tròn đến cm (cho \(\pi = 3,14\))
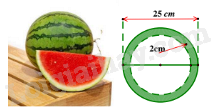
Giả sử một quả dưa hấu không hạt ruột đỏ dạng hình cầu có đường kính 25cm và phần vỏ dày 2cm. Tính diện tích phần ruột trắng của mặt cắt trái dưa hấu đó.
Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 8 cm) và (O; 24 cm).
Một ống thép có đường kính ngoài là 100 mm và đường kính trong là 80 mm. Tính diện tích mặt cắt ngang của ống thép đó.
Hình vành khuyên giới hạn bởi hai đường tròn (O; 5 cm) và (O’; 2 cm) có diện tích (lấy \(\pi \) theo máy tính và kết quả làm tròn đến hàng phần trăm) là
A. 131,94 cm2
B. 18,84 cm2
C. 9,42 cm2
D. 65,97 cm2.
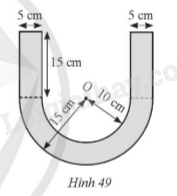
Hình 49 mô tả mặt cắt của một chi tiết máy ép nhựa có dạng ở giữa là nửa hình vành khuyên giới hạn bởi hai nửa đường tròn (O; 15 cm), (O; 10 cm) và hai đầu là hai hình chữ nhật có chiều dài 15 cm, chiều rộng 5 cm. Tính diện tích mặt cắt của chi tiết máy ép nhựa đó (làm tròn kết quả đến hàng phần trăm của centimét vuông).
Diện tích hình vành khuyên tạo bởi hai đường tròn (O; 12 cm) và (O; 7 cm) là:
A. \(95\pi cm^2\).
B. \(193\pi cm^2\).
C. \(5\pi cm^2\).
D. \(19\pi cm^2\).
Cho hình vành khuyên giới hạn bởi hai đường tròn (O; R), (O; r) với \(R + r = 1,2dm\), \(R > r\) và diện tích hình vành khuyên đó là 1,5072 dm2 (Hình 55). Tính R và r, \(\pi \approx 3,14\).
Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 2cm) và (O; 4cm) là
A. \(2\pi \;c{m^2}\).
B. \(4\pi \;c{m^2}\).
C. \(12\pi \;c{m^2}\).
D. \(16\pi \;c{m^2}\).
Tính diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính là 6cm và 4cm.
