Cho hình chóp SABCD có đáy là hình chữ nhật với \(AB = a,AD = 2a\). Biết \(SA \bot \left( {ABCD} \right)\) và \(SA = a\sqrt {15} \). Tính góc giữa SC và mặt phẳng \(\left( {ABCD} \right)\).
-
A.
\(30^\circ \).
-
B.
\(60^\circ \).
-
C.
\(45^\circ \).
-
D.
\(90^\circ \).
Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
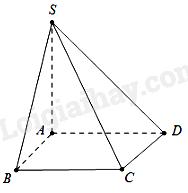
\((SC,\widehat {(ABD})) = (SC;\widehat {(ABCD})) = (\widehat {SC;AC}) = \widehat {SCA}.\)
Xét tam giác vuông SAC, ta có:
\(\tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{{SA}}{{\sqrt {A{B^2} + B{C^2}} }} = \frac{{a\sqrt {15} }}{{\sqrt {{a^2} + {{(2a)}^2}} }} = \sqrt 3 .\)
Suy ra \(\widehat {SCA} = {60^\circ }\).
Đáp án B.
Đáp án : B
Các bài tập cùng chuyên đề
Cho số thực \(x > 0\), biểu thức \(\sqrt[3]{{{x^2}\sqrt x }}\) bằng
Đạo hàm của hàm số \(f\left( x \right) = {\log _2}\left( {{x^2} + 1} \right)\) là
Tính đạo hàm của hàm số \(y = \frac{{x + 6}}{{x + 9}}\):
Tập nghiệm của phương trình \({\rm{lo}}{{\rm{g}}_3}\left( {{x^2} - 7} \right) = 2\) là
Giải phương trình \(f''\left( x \right) = 0\), biết \(f\left( x \right) = {x^3} - 3{x^2}\).
Đạo hàm của hàm số \(y = 2{{\rm{x}}^2} - 3{\rm{x}} + 7\) là:
Cho A,B là hai biến cố xung khắc. Đẳng thức nào sau đây đúng?
Cho hình chóp S.ABC có đáy ABC vuông cân tại B,\(AB = BC = a,SA = a\sqrt 3 ,\)\(SA \bot \left( {ABC} \right)\). Số đo của góc phẳng nhị diện \(\left[ {S,BC,A} \right]\) là
Hàm số \(y = {\cos ^2}3x\) có đạo hàm là
Hai người độc lập nhau ném bóng vào rổ. Mỗi người ném vào rổ của mình một quả bóng. Biết rằng xác suất ném bóng trúng vào rổ của từng người tương ứng là \(\frac{1}{5}\) và \(\frac{2}{7}\). Gọi \(A\) là biến cố: "Cả hai cùng ném bóng trúng vào rổ". Khi đó, xác suất của biến cố \(A\) là bao nhiêu?
Tìm tọa độ tiếp điểm của các tiếp tuyến \(\Delta \) với đồ thị của hàm số \(y = \frac{{x - 1}}{{x + 1}}\), biết tiếp tuyến đó song song với đường thẳng \(2x - y - 1 = 0\).
Cho khối lăng trụ tam giác đều ABC.A'B'C' có độ dài cạnh đáy bằng \(a\) và đường thẳng A'B hợp với mặt đáy một góc \(60^\circ \). Tính thể tích \(V\) của khối lăng trụ ABC.A'B'C'.
Cho khối chóp có diện tích đáy bằng \(7{a^2}\) và chiều cao bằng 9a. Thể tích của khối chóp đã cho bằng
Cho chuyển động thẳng xác định bởi phương trình \(s = {t^3} - 3{t^2} - 9t\), trong đó \(t > 0,t\) tính bằng giây và \({\rm{s}}({\rm{t}})\) tính bằng mét. Gia tốc của chuyển động tại thời điểm vận tốc bị triệt tiêu là: …………………………………………………………………
Cho A, B là hai biến cố. Biết \({\rm{P}} = \frac{1}{2},{\rm{P}}(B) = \frac{3}{4};{\rm{P}}(A \cap B) = \frac{1}{4}\). Khi đó: \(P\left( {A \cup B} \right)\) bằng: …………..
Gọi \(S\) là tập hợp gồm 6 số lẻ và 4 số chẵn. Chọn ngẫu nhiên 3 số từ \(S\), xác suất để 3 số chọn ra có tích là số chẵn bằng:…………………………………………………………………………………………….
Cho khối lăng trụ tam giác đều \(ABC \cdot A'B'C'\) có độ dài cạnh đáy bằng \(a\) và đường thẳng \(A'B\) hợp với mặt đáy một góc \(60^\circ \). Tính thể tích \(V\) của khối lăng trụ \(ABC \cdot A'B'C'\) bằng:………………………….
Phương trình \({27^{2x - 3}} = {\left( {\frac{1}{3}} \right)^{{x^2} + 2}}{\rm{ }}{\mkern 1mu} \) có tập nghiệm là:…………………………………………………..
