Cho hai tia \({\rm{Ox}},{\rm{Oy}}\) đối nhau. Trên tia \({\rm{Ox}}\) lấy điểm \({\rm{A}}\) sao cho \({\rm{OA}} = 4\;{\rm{cm}}\). Trên tia \({\rm{Oy}}\) lấy điểm \({\rm{B}}\) sao cho \({\rm{OB}} = 2\;{\rm{cm}}\). Gọi \({\rm{C}}\) là trung điểm của đoạn thẳng \({\rm{OA}}\).
a) Tính độ dài đoạn thẳng \({\rm{AB}}\).
b) Điểm \({\rm{O}}\) có là trung điểm của đoạn thẳng \({\rm{BC}}\) không? Vì sao?
c) Vẽ tia \({\rm{Oz}}\) khác các tia \({\rm{Ox}},{\rm{Oy}}\). Viết tên các góc có trong hình vẽ.
Vẽ hình theo hướng dẫn.
a) Xác định độ dài đoạn thẳng AB qua OA và OB.
b) Chứng minh OB = OC và O nằm giữa B và C nên O là trung điểm của BC.
c) Vẽ tia Oz và kể tên các góc trong hình.
Vẽ hình
a) Theo hình vẽ: \(AB = OA + OB = 4 + 2 = 6\;{\rm{cm}}\)
Vậy \(AB = 6\;{\rm{cm}}\)
b) Vì C là trung điểm của đoạn thẳng \({\rm{OA}}\) nên \(OC = \frac{{OA}}{2} = \frac{4}{2} = 2\;{\rm{cm}}\)
Suy ra \({\rm{OB}} = {\rm{OC}}\)
Lại có \({\rm{O}}\) nằm giữa \({\rm{B}}\) và \({\rm{C}}\)
Do đó O là trung điểm của đoạn thẳng \({\rm{BC}}\)
Vậy \({\rm{O}}\) là trung điểm của đoạn thẳng \({\rm{BC}}\).
c)
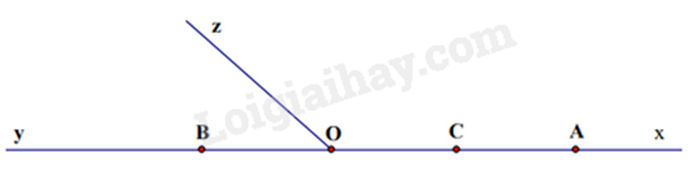
Các góc có trong hình vẽ là:
\(\widehat {{\rm{xOz}}};\widehat {{\rm{yOz}}};\widehat {{\rm{xOy}}},\widehat {xAy},\widehat {xCy},\widehat {xBy}\)
Các bài tập cùng chuyên đề
Cách viết nào sau đây không phải phân số?
Số đối của phân số \(\frac{{ - 15}}{{16}}\) là
Số nguyên \(x\) thỏa mãn điều kiện \(\frac{x}{3} = \frac{6}{{ - 9}}\) là
Tỉ số phần trăm của 16 và 20 là
Nam mua một quyển sách có giá bìa là 50000 đồng. Khi trả tiền được cửa hàng giảm giá \(10\% \). Hỏi Nam mua quyển sách đó hết bao nhiêu tiền?
Làm tròn số 131,2956 đến hàng phần trăm được kết quả là
Biết \(\frac{3}{5}\) của một số bằng (-30), số đó là
Dữ liệu nào sau đây là số liệu?
Khi gieo một đồng xu 15 lần. Nam thấy có 9 lần xuất hiện mặt ngửa. Xác suất thực nghiệm của sự kiện xuất hiện mặt sấp là
Hai tia đối nhau trong hình vẽ dưới đây là
Trên đường thẳng a lấy 10 điểm phân biệt. Số đoạn thẳng trong hình vẽ là:
Lúc 10 giờ, góc tạo bởi kim giờ và kim phút là:
1) Thực hiện phép tính:
a) \(\frac{1}{4} + \frac{3}{4} \cdot \left( {\frac{2}{3} - 0,5} \right)\)
b) \(1\frac{3}{{25}} - \frac{{17}}{{19}} - \frac{3}{{25}} + \frac{{2022}}{{2023}} - \frac{2}{{19}}\)
2) Tìm \(x\) biết:
a) \(\frac{2}{3}x - \frac{1}{2} = \frac{1}{{10}}\)
b) \(5,16 - 2x = (5,7 + 2,3) \cdot ( - 0,3)\)
Lớp 6A có 40 học sinh, học lực cuối học kì II được xếp thành ba loại tốt, khá và đạt. Số học sinh xếp loại tốt chiếm \(\frac{2}{5}\) số học sinh cả lớp, số học sinh xếp loại khá bằng \(\frac{5}{8}\) số học sinh còn lại.
a) Tính số học sinh mỗi loại của lớp?
b) Hỏi số học sinh xếp loại đạt chiếm bao nhiêu phần trăm của lớp?
Bạn Linh gieo một con xúc sắc 100 lần và ghi lại số chấm xuất hiện ở mỗi lần gieo được kết quả như sau:
a) Hỏi mặt mấy chấm xuất hiện nhiều nhất;
b) Tính xác suất thực nghiệm của sự kiện số chấm xuất hiện là số chẵn.
So sánh S với 2, biết \(S = \frac{1}{2} + \frac{2}{{{2^2}}} + \frac{3}{{{2^3}}} + \ldots + \frac{{2023}}{{{2^{2023}}}}\).
