Đề bài

Cho tam giác ABC cân tại A. Kẻ \(BH \bot AC;CK \bot AB\) (\(H \in AC;\,\)\(K \in AB\)).

a) Chứng minh tam giác AKH là tam giác cân

b) Gọi I là giao của BH và CK; AI cắt BC tại M. Chứng minh rằng IM là phân giác của \(\widehat {BIC}\).

c) Chứng minh: \(HK\,{\rm{//}}\,BC\).

Phương pháp giải

a) Chứng minh \(\Delta ABH = \Delta ACK\) theo trường hợp cạnh huyền – góc nhọn. suy ra AH = AK nên tam giác AKH là tam giác cân.

b) Chứng minh \(\widehat {{P_1}} = \widehat {{N_1}}\) nên \(\Delta AKI = \Delta AHI\) theo trường hợp cạnh huyền – cạnh góc vuông suy ra \(\widehat {AIK} = \widehat {AIH}\)

Từ đó ta có \(\widehat {CIM} = \widehat {BIM}\) nên IM là phân giác của góc BIC

c) Từ tam giác cân ABC và AHK ta có \(\widehat {ABC} = \frac{{180^\circ - \widehat A}}{2}\), \(\widehat {AKH} = \frac{{180^\circ - \widehat A}}{2}\) nên \(\widehat {ABC} = \widehat {AKH}\).

Mà hai góc này ở vị trí đồng vị nên HK // BC.

Lời giải của GV Loigiaihay.com

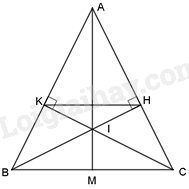
a) Xét \(\Delta ABH\) và \(\Delta ACK\) có:

\(\widehat {AHB} = \widehat {AKC} = 90^\circ \) (vì \(BH \bot AC;CK \bot AB\))

AB = AC (\(\Delta ABC\) cân);

góc A chung;

Do đó: \(\Delta ABH = \Delta ACK\) (cạnh huyền – góc nhọn).

\( \Rightarrow AH = AK \Rightarrow \Delta AHK\) cân tại A (đpcm).

b) Xét \(\Delta AKI\) và \(\Delta AHI\) có: \(\widehat {AKI} = \widehat {AHI} = 90^\circ \) (vì \(BH \bot AC;CK \bot AB\))

AK = AH (\(\Delta AHK\) cân tại A);

cạnh AI chung;

Do đó: \(\Delta AKI = \Delta AHI\) (cạnh huyền – cạnh góc vuông).

\( \Rightarrow \widehat {AIK} = \widehat {AIH}\).

Mà: \(\widehat {AIK} = \widehat {CIM};\widehat {AIH} = \widehat {BIM}\) (2 góc đối đỉnh).

Do đó: \(\widehat {CIM} = \widehat {BIM}\)\( \Rightarrow IM\)là phân giác của góc BIC (đpcm).

c) \(\Delta ABC\) cân tại A nên: \(\widehat {ABC} = \frac{{180^\circ - \widehat A}}{2}\) .

\(\Delta AHK\) cân tại A nên: \(\widehat {AKH} = \frac{{180^\circ - \widehat A}}{2}\) .

Suy ra \(\widehat {ABC} = \widehat {AKH}\).

Mà 2 góc này ở vị trí đồng vị.

Do đó: KH // BC (đpcm).

Báo lỗi/Góp ý

Các bài tập cùng chuyên đề

Bài 1 :

Trong các phát biểu sau, phát biểu nào đúng?