Có hai chiếc cột dựng thẳng đứng trên mặt đất với chiều cao lần lượt là 5 m và 3 m. Người ta nối hai sợi dây từ đỉnh cột này đến chân cột kia và hai sợi dây cắt nhau tại một điểm. Tính độ cao ℎ của điểm đó so với mặt đất.
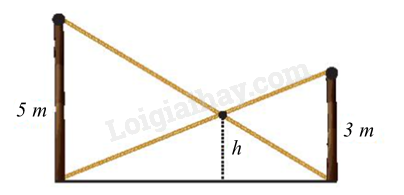
- Theo đề bài vẽ lại hình và đặt tên các điểm.
- Chứng minh các tam giác đồng dạng và suy ra các tỉ số đồng dạng để tính độ cao của h.
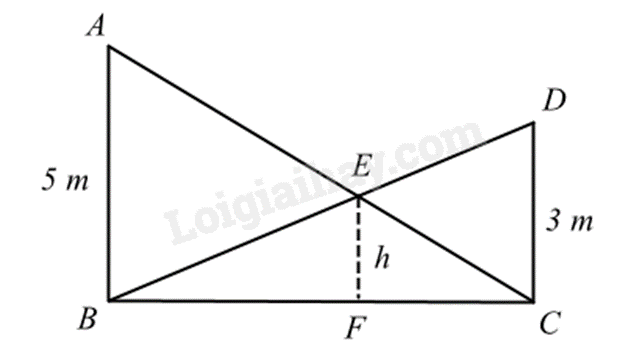
Ta có: AB // CD nên \(\widehat {BAC} = \widehat {DCA}\) và \(\widehat {ABD} = \widehat {CDB}\) (hai góc so le trong)
Xét \(\Delta ABE\) và \(\Delta CDE\) có:
\(\begin{array}{l}\widehat {BAC} = \widehat {DCA}\\\widehat {ABD} = \widehat {CDB}\end{array}\)
Suy ra $\Delta ABE\backsim \Delta CDE$ (gg)
Suy ra \(\frac{{CE}}{{AE}} = \frac{{CD}}{{AB}} = \frac{3}{5}\)
Suy ra \(\frac{{CE}}{{AC}} = \frac{3}{8}\)
Xét \(\Delta CFE\) và \(\Delta CBA\) có:
\(\widehat C\) chung
\(\widehat {ABC} = \widehat {EFC}\)
suy ra $\Delta CFE\backsim \Delta CBA$ (g.g)
suy ra \(\frac{{EF}}{{AB}} = \frac{{CE}}{{AC}} = \frac{3}{8}\). Do đó \(EF = \frac{3}{8}.AB = \frac{3}{8}.5 = \frac{{15}}{8}\) (m)
Các bài tập cùng chuyên đề
Cho công thức \(C = \frac{5}{9}\left( {F - 32} \right)\) với C = 10. Tính \(F\), ta được kết quả:
Cho $\Delta ABC\backsim \Delta DEF$ theo tỉ số đồng dạng \(\frac{1}{2}\) thì tỉ số hai đường cao tương ứng là:
Một mô hình ô tô dài 12cm. Thực tế ô tô dài 2,4m. Tỉ số đồng dạng của mô hình và vật thật là:
Cho tam giác ABC nhọn (AB < AC) có hai đường cao BE, CF cắt nhau tại H
a) Chứng minh $\Delta ABE\backsim \Delta ACF$
b) Đường thẳng qua E song song với AB, cắt đoạn CH tại D. Chứng minh \(H{E^2} = HD.HC\).
c) Gọi I là trung điểm của CB. Các đường thẳng kẻ từ B song song với CF và từ C song song với BE cắt nhau tại K. Chứng minh H, I, K thẳng hàng.
