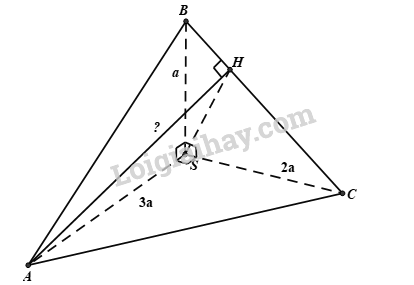
Cho tứ diện SABC trong đó SA, SB, SC vuông góc với nhau từng đôi một và SA = 3a, SB = a, SC = 2a. Khoảng cách từ A đến BC bằng?
-
A.
\(\frac{{3a\sqrt 2 }}{2}\).
-
B.
\(\frac{{7a\sqrt 5 }}{5}\).
-
C.
\(\frac{{8a\sqrt 3 }}{3}\).
-
D.
\(\frac{{5a\sqrt 6 }}{6}\).
Sử dụng phương pháp tính khoảng cách từ đường thẳng tới mặt phẳng
Dựng \(AH \bot BC \Rightarrow d(A,BC) = AH\)
\(\begin{array}{l}\left\{ \begin{array}{l}SA \bot (SBC)\\AH \bot BC\end{array} \right. \Rightarrow SA \bot BC\\ \Rightarrow BC \bot (SAH) \Rightarrow BC \bot SH\end{array}\)
Xét tam giác SBC vuông tại S có SH là đường cao ta có:
\(\begin{array}{l}\frac{1}{{S{H^2}}} = \frac{1}{{S{B^2}}} + \frac{1}{{S{C^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{4{a^2}}} = \frac{5}{{4{a^2}}} \Rightarrow S{H^2} = \frac{{4{a^2}}}{5}\\ \Rightarrow SH = \frac{{2a\sqrt 5 }}{5}\end{array}\)
Ta có: \(SA \bot (SBC) \Rightarrow SA \bot SH \Rightarrow \Delta SAH\)vuông tại S
Áp dụng hệ thức lượng trong \(\Delta SAH\) vuông tại S ta có:
\(A{H^2} = S{A^2} + S{H^2} = 9{a^2} + \frac{{4{a^2}}}{5} = \frac{{49{a^2}}}{5} \Rightarrow AH = \frac{{7a\sqrt 5 }}{5}\)
Đáp án B.
Đáp án : B
Các bài tập cùng chuyên đề
Tính giá trị của biểu thức \(A = \frac{{{{12}^{5 + \sqrt 3 }}}}{{{2^{5 + 2\sqrt 3 }}{{.3}^{7 + \sqrt 3 }}}}\):
Trong các hình sau, hình nào là dạng đồ thị của hàm số \(y = {\log _a}x,0 < a < 1\)
Cho hình chóp \(SABC\) có \(SA \bot \left( {ABC} \right).\) Gọi \(H,{\rm{ }}K\) lần lượt là trực tâm các tam giác \(SBC\) và\(ABC\). Mệnh đề nào sai trong các mệnh đề sau?
Tại một cuộc hội thảo quốc tế có 50 nhà khoa học trong đó có 31 người thành thạo tiếng Anh, 21 người thành thạo tiếng Pháp và 5 người thành thạo cả tiếng Anh và tiếng Pháp. Chọn ngẫu nhiên một người dự hội thảo. Xác suất để người được chọn thành thạo ít nhất một trong hai thứ tiếng Anh hoặc tiếng Pháp là:
Cho hàm số \(y = - {x^3} + 3x - 2\) có đồ thị \(\left( C \right).\)Phương trình tiếp tuyến của \(\left( C \right)\) tại giao điểm của \(\left( C \right)\) với trục tung là
Cho hàm số \(y = {\sin ^2}x\). Khi đó đạo hàm y’ là
Hàm số \(y = \sqrt {2 + 2{x^2}} \)có đạo hàm \(y' = \frac{{a + bx}}{{\sqrt {2 + 2{x^2}} }}\). Khi đó \(S = a - 2b\) có kết quả bằng
Hàm số \(y = \frac{{{x^2} + x}}{{x - 1}}\)có đạo hàm \(y' = \frac{{a{x^2} + bx + c}}{{{{(x - 1)}^2}}}\). Khi đó \(S = a + b + c\) có kết quả là:
Một chất điểm chuyển động có phương trình \(s\left( t \right) = {t^2} + 1\) (\(t\) tính bằng giây, \(s\) tính bằng mét). Vận tốc tức thời của chất điểm tại thời điểm \(t = 3s\)bằng
Hai người cùng bắn vào 1 bia. Người thứ nhất có xác suất bắn trúng là 60%, xác suất bắn trúng của người thứ 2 là 70%. Xác suất để cả hai người cùng bắn trật bằng:
Hàm số \(y = {x^5}\) có đạo hàm là:
