Cho hình chóp tứ giác đều S.ABCD. Đáy ABCD là hình vuông tâm O, gọi I là trung điểm của cạnh AD. Hỏi góc giữa 2 mặt phẳng (SAD) và (ABCD) là:
-
A.
\(\widehat {SIO}\)
-
B.
\(\widehat {SOI}\)
-
C.
\(\widehat {OSI}\)
-
D.
\(\widehat {SAO}\)
Sử dụng phương tính xác định góc giữa hai mặt phẳng
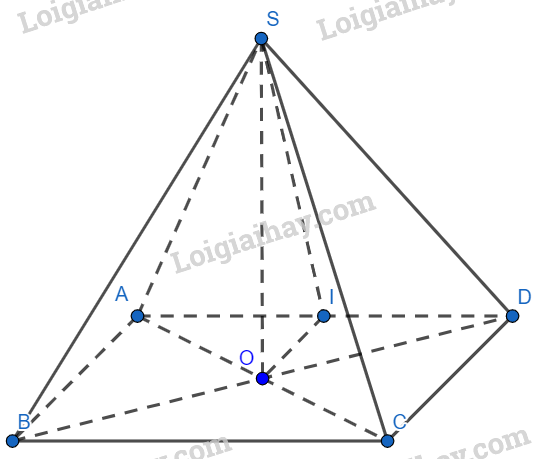
Xét tam giác ADC có: OI là đường trung bình
Suy ra: \(OI//CD\) (tính chất đường trung bình)
Do ABCD là hình vuông nên \(CD \bot AD\)
Suy ra: \(OI \bot AD\)
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}AD \bot OI - cmt\\AD \bot SO\,\,(SO \bot (ABCD))\\OI,SO \subset (SOI)\\OI \cap SO\end{array} \right. \Rightarrow AD \bot (SOI)\\ \Rightarrow AD \bot SI\end{array}\)
Ta có:
\(\left\{ \begin{array}{l}(SAD) \cap (ABCD) = AD\\SI \subset (SAD),SI \bot AD\\OI \subset (ABCD),OI \bot AD\end{array} \right. \Rightarrow \left( {(SAD),(ABCD)} \right) = (SI,OI)\)
Xét tam giác SOI vuông tại O: \((SI,OI) = \widehat {SOI}\)
Đáp án B.
Đáp án : B
