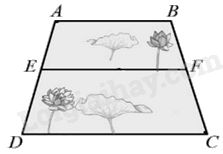
Một ao sen có dạng hình thang \(ABCD\left( {AB//CD} \right)\) với \(AB = 35{\rm{\;m}},CD = 56{\rm{\;m}}\). Người ta chọn một vị trí \(E\) ở trên bờ \({\rm{AD}}\) sao cho \(AE = \frac{3}{4}ED\) và bắc một cây cầu \({\rm{EF}}\) song song với hai bờ \(AB,CD\left( {F \in BC} \right)\). Để mọi người có thể đi trên cầu buổi tối ngắm sen, người ta căng đèn trang trí dọc theo cây cầu đó với khoảng cách giữa hai chiếc đèn liên tiếp là \(2{\rm{\;m}}\) và cả hai đầu cầu đều có đèn. Tính số tiền cần dùng để mua đèn trang trí cho cây cầu đó, biết giá mỗi chiếc đèn là 15000 đồng.
-
A.
345000 đồng
-
B.
330000 đồng
-
C.
300000 đồng
-
D.
310000 đồng
Áp dụng hệ quả của định lí Thales: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
Áp dung định lí Thales: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Gọi \(M\) là giao điểm của \({\rm{AC}}\) và \({\rm{EF}}\).
Chứng minh được: \(\frac{{MF}}{{AB}} = \frac{{MC}}{{AC}} = \frac{{DE}}{{DA}};\frac{{AE}}{{AD}} = \frac{{EM}}{{DC}}\)
Từ đó tính được \({\rm{ME}},{\rm{MF}},{\rm{EF}}\)
Tính số bóng đèn bằng \(\left( {EF:2} \right) + 1\)
Tính số tiền mua bóng đèn.
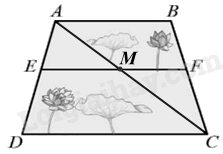
Gọi \(M\) là giao điểm của \({\rm{AC}}\) và \({\rm{EF}}\).
Vì \(AE = \frac{3}{4}ED\) nên \(\frac{{AE}}{3} = \frac{{ED}}{4} = \frac{{AE + ED}}{{3 + 4}} = \frac{{AD}}{7}\) suy ra \(\frac{{AE}}{{AD}} = \frac{3}{7};\frac{{ED}}{{AD}} = \frac{4}{7}\)
Xét \(\Delta ACD,ME//CD\) suy ra \(\frac{{AE}}{{AD}} = \frac{{EM}}{{CD}}\) (hệ quả của định lí Thales) nên \(\frac{{ME}}{{56}} = \frac{3}{7}\) hay \(ME = 24{\rm{\;m}}\).
\(\frac{{MC}}{{AC}} = \frac{{DE}}{{DA}}\) (định lí Thales) (1)
Xét \(\Delta ABC,MF//AB\) nên \(\frac{{MC}}{{AC}} = \frac{{MF}}{{AB}}\) (định lí Thales) (2)
Từ (1), (2) suy ra \(\frac{{MF}}{{AB}} = \frac{{DE}}{{DA}}\) hay \(\frac{{MF}}{{35}} = \frac{4}{7}\) suy ra \(MF = 20{\rm{\;m}}\).
Ta có \(EF = ME + MF = 24 + 20 = 44\left( {{\rm{\;m}}} \right)\).
Số chiếc đèn cần dùng để trang trí dọc theo cây cầu EF là: \(\left( {44:2} \right) + 1 = 23\).
Số tiền cần dùng để mua đèn trang trí cho cây cầu đó là: \(15000.23 = 345000\) (đồng).
Đáp án A.
Đáp án : A
Các bài tập cùng chuyên đề
Cho tam giác \({\rm{ABC}}\) có \(AB = 4,5{\rm{\;cm}},AC = 6{\rm{\;cm}}\). Các điểm \({\rm{M}},{\rm{N}}\) lần lượt thuộc các cạnh \({\rm{AB}},{\rm{AC}}\) thoả mãn \(AM = 3{\rm{\;cm}}\) và \(MN\parallel BC\). Tính độ dài đoạn thẳng \({\rm{AN}}\).
Chọn phát biểu đúng.
Đáp án nào dưới đây không là phương trình bậc nhất một ẩn?
Cho các đường thẳng \({d_1}:y = 11x + 1;{d_2}:y = \sqrt 3 x - 7;{d_3}:y = 2x - \sqrt 2 \). Gọi \({\alpha _1},{\alpha _2},{\alpha _3}\) lần lượt là các góc tạo bởi đường thẳng \({d_1},{d_2},{d_3}\) và trục \({\rm{Ox}}\). Sắp xếp các góc \({\alpha _1},{\alpha _2},{\alpha _3}\) theo thứ tự số đo tăng dần.
Cho hai đường thẳng \(d:y = mx - \left( {2m + 2} \right)\) và \(d':y = \left( {3 - 2m} \right)x + 1\) với \(m \ne 0\) và \(m \ne \frac{3}{2}\) Tìm giá trị của \(m\) để \(d\) và \(d\) ' cắt nhau.
Cho hình sau với tam giác \({\rm{ABC}}\) có \(AB = AC = 9{\rm{\;cm}}\) và tia phân giác của góc \(B\) cắt đường cao \({\rm{AH}}\) ở \(I\) Biết \(\frac{{AI}}{{IH}} = \frac{3}{2}\). Tính chu vi tam giác \({\rm{ABC}}\).
Câu ca dao "Lúa chiêm lấp ló đầu bờ - Hễ nghe tiếng sấm phất cờ mà lên" về mặt khoa học được giải thích như sau: Khi trời mưa kèm theo sấm sét, nitric acid sẽ được sinh ra và hoà tan trong nước mưa, có tác dụng làm tăng cường dinh dưỡng nitrogen cho đất trồng, giúp cây lúa phát triển tươi tốt. Phân tử của nitric acid đó có một nguyên tử \({\rm{H}}\), một nguyên tử \({\rm{N}}\) và \(x\) nguyên tử \({\rm{O}}\). Xác định công thức phân tử của nitric acid đó. Biết khối lượng phân tử của nó là 63amu và khối lượng của mỗi nguyên tử \({\rm{H}},{\rm{N}},{\rm{O}}\) lần lượt là 1amu, 14amu, 16amu .
Trong hội thi STEM của một trường trung học cơ sở, ban tổ chức đưa ra quy tắc chấm thi cho bài thi gồm 30 câu hỏi như sau: Với mỗi câu hỏi, nếu trả lời đúng thì được 5 điểm, nếu trả lời không đúng thì không được điểm, nếu không trả lời thì được 1 điểm. Một học sinh làm bài thi và có số câu trả lời đúng gấp 3 lần số câu trả lời không đúng, kết quả đạt 85 điểm. Hỏi bài thi của học sinh đó có bao nhiêu câu trả lời đúng? Bao nhiêu câu trả lời không đúng? Bao nhiêu câu không trả lời?
Giải các phương trình sau:
a) \(1,5\left( {x - 5} \right) + 11 = 7\left( {x - 8} \right) - 50,5\);
b) \(\frac{{x - 4}}{5} + \frac{{3x - 2}}{{10}} - x = \frac{{2x - 5}}{3} - \frac{{7x + 2}}{6}\);
c) \(\frac{{x + 1}}{3} - \frac{{3\left( {2x + 1} \right)}}{4} - \frac{{5x + 3}}{6} = x + \frac{7}{{12}}\).
Để sử dụng thẻ dịch vụ nghì dưỡng 5 sao ở bãi biển Nha Trang của một công ty du lịch, khách hàng phải trả phí thuê theo ngày và một khoản phí ban dầu gọi là phí duy trì thẻ. Một phần đường thẳng \({\rm{d}}\) ở hình sau biểu thị tổng chi phí (đơn vị: triệu đồng) mà khách hàng đó phài trả để sử dụng dịch vụ của công ty du lịch theo thời gian nghỉ dưỡng (đơn vị: ngày)
a) Tìm hàm số bậc nhất sao cho đồ thị của hàm số là đường thẳng \({\rm{d}}\).
b) Tính tổng chi phí mà khách hàng đó phải trả khi sử dụng thẻ dịch vụ nghỉ dưỡng trên trong thời gian 4 ngày
Hình tam giác và hình chữ nhật dưới đây có cùng chu vi. Viết phương trình biểu thị sự bằng nhau của chu vi hình tam giác, hình chữ nhật đó và tìm \(x\).
