Cho \(A = \left( {\frac{{2x - 1}}{{x + 3}} + \frac{x}{{x - 3}} - \frac{{3 - 10x}}{{{x^2} - 9}}} \right):\frac{{x + 2}}{{x - 3}}\)
a) Tìm điều kiện xác định của \(A\) và rút gọn \(A\)
b) Tìm \(x\) nguyên để \(A\) có giá trị nguyên
Điều kiện xác định của phân thức là mẫu thức khác 0 .
Rút gọn biểu thức bằng cách thực hiện các phép toán cộng, trừ, nhân, chia phân thức.
a) ĐКXĐ: \(\left\{ {\begin{array}{*{20}{l}}{x + 3 \ne 0}\\{x - 3 \ne 0}\\{{x^2} - 9 \ne 0}\\{x + 2 \ne 0}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x \ne \pm 3}\\{x \ne - 2}\end{array}} \right.} \right.\)
\(A = \left( {\frac{{2x - 1}}{{x + 3}} + \frac{x}{{x - 3}} - \frac{{3 - 10x}}{{{x^2} - 9}}} \right):\frac{{x + 2}}{{x - 3}}\)
\(A = \frac{{\left( {2x - 1} \right)\left( {x - 3} \right) + x\left( {x + 3} \right) - \left( {3 - 10x} \right)}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} \cdot \frac{{x - 3}}{{x + 2}}\)
\(A = \frac{{2{x^2} - 6x - x + 3 + {x^2} + 3x - 3 + 10x}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} \cdot \frac{{x - 3}}{{x + 2}}\)
\(A = \frac{{3{x^2} + 6x}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} \cdot \frac{{x - 3}}{{x + 2}}\)
\(A = \frac{{3x\left( {x + 2} \right)}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} \cdot \frac{{x - 3}}{{x + 2}}\)
\(A = \frac{{3x}}{{x + 3}}\)
b) \(A = \frac{{3x}}{{x + 3}} = \frac{{3\left( {x + 3} \right) - 9}}{{x + 3}} = 3 - \frac{9}{{x + 3}}\)
Để nhận giá trị nguyên thì \(\frac{9}{{x + 3}}\) nguyên \( \Rightarrow 9:\left( {x + 3} \right) \Rightarrow x + 3 \in U\left( 9 \right)\)
Ta có bảng sau:
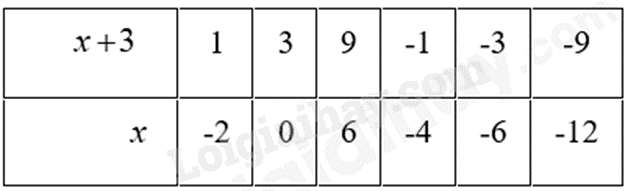
Đối chiếu ĐKXĐ ta được \(x \in \left\{ { - 12, - 6, - 4,0,6} \right\}\)
Vậy \(x \in \left\{ { - 12, - 6, - 4,0,6} \right\}\) thì \(A\) nhận giá trị nguyên.
Các bài tập cùng chuyên đề
Tìm khẳng định sai:
Phương trình nào sau đây nhận \(x = 3\) làm nghiệm?
Cho tam giác \({\rm{ABC}}\) và hai điểm \({\rm{M}},{\rm{N}}\) lần lượt thuộc các cạnh \({\rm{BC}},{\rm{AC}}\) sao cho \({\rm{MN}}\) // AB. Chọn kết luận đúng.
Cho hình bên biết \({\rm{AB}} = 6{\rm{\;cm}},{\rm{AC}} = 9{\rm{\;cm}},\widehat {ABD} = \widehat {BCA}\). Thế thì độ dài \({\rm{AD}}\) là:
Một ca nô xuôi dòng từ bến \(A\) đến bến \(B\) mất 4 giờ và ngược dòng từ \(B\) về \(A\) mất 5 giờ. Biết vận tốc riêng của ca nô luôn giữ không đổi là \(18{\rm{\;km}}/{\rm{h}}\). Tính vận tốc của dòng nước.
Cho hình vẽ, chỉ ra hai cặp tam giác đồng dạng.
Chọn đa thức thích hợp vào chỗ trống cho đẳng thức sau: \(\frac{{{x^3} + 8}}{{x + 2}} = \frac{ \ldots }{2}\)
Mẫu thức của phân thức \(\frac{{{x^2} - xy - x + y}}{{{x^2} + xy - x - y}}\) sau khi thu gọn có thể là:
Nghiệm của phương trình \(\frac{{x + 5}}{2} - \frac{1}{3} = \frac{{3 - 2x}}{6}\) là:
Cho \(A = \frac{{2x - 1}}{{6{x^2} - 6x}} - \frac{3}{{4{x^2} - 4}}\). Phân thức thu gọn của \(A\) có tử thức là:
Thực hiện phép tính:
a) \(\frac{{2x + 5}}{{5{x^2}{y^2}}} + \frac{8}{{5x{y^2}}} + \frac{{2x - 1}}{{{x^2}{y^2}}}\)
b) \(\frac{{4{x^2} - 3x + 5}}{{{x^3} - 1}} - \frac{{1 - 2x}}{{{x^2} + x + 1}} - \frac{6}{{x - 1}}\)
c) \(\frac{{{x^4} + 4{x^2} + 5}}{{5{x^3} + 5}} \cdot \frac{{2x}}{{{x^2} + 4}} \cdot \frac{{3{x^3} + 3}}{{{x^4} + 4{x^2} + 5}}\)
d) \(\frac{{5x + 1}}{{2x - 3}} \cdot \frac{{x + 2}}{{25{x^2} - 1}} - \frac{{8 - 3x}}{{25{x^2} - 1}} \cdot \frac{{5x + 1}}{{2x - 3}}\)
Trong học kì I, số học sinh giỏi của lớp 8A bằng \(\frac{1}{8}\) số học sinh cả lớp. Sang học kì II, lớp có thêm 3 học sinh giỏi nữa, khi đó số học sinh giỏi trong học kì II bằng \(20{\rm{\% }}\) số học sinh cả lớp. Hỏi lớp \(8{\rm{\;A}}\) có bao nhiêu học sinh?
Hình thang \({\rm{ABCD}}\) ở hình dưới đây có \(AB//CD\), \(AB < CD,\widehat {ABD} = {90^0}\). Hai đường chéo \({\rm{AC}}\) và \({\rm{BD}}\) cắt nhau tại \(G\). Điểm \(E\) nằm trên đường vuông góc với \({\rm{AC}}\) tại \(C\) thoả mãn \(CE = AG\) và đoạn thẳng \({\rm{GE}}\) không cắt đường thẳng \({\rm{CD}}\). Điểm \(F\) nằm trên đoạn thẳng \({\rm{DC}}\) và \(DF = GB\). Chứng minh:
a) $\Delta FDG\backsim \Delta ECG$
b) $\Delta GDC\backsim \Delta GFE$;
c) \(\widehat {GFE} = {90^0}\).
Cho \(x;y;z \ne 0\) thỏa mãn \(\frac{{x - y - z}}{x} = \frac{{y - z - x}}{y} = \frac{{z - x - y}}{z}\).
Tính giá trị biểu thức: \(S = \left( {1 + \frac{y}{x}} \right)\left( {1 + \frac{z}{y}} \right)\left( {1 + \frac{x}{z}} \right)\).
