Cho hình thang \({\rm{ABCD}}\left( {AB\parallel CD} \right)\) có \(\widehat {ABD} = \widehat {BDC},AB = 2{\rm{\;cm}},BD = \sqrt 5 \), ta có:
-
A.
\(CD = 2\sqrt 5 {\rm{\;cm}}\)
-
B.
\(CD = \sqrt 5 - 2{\rm{\;cm}}\)
-
C.
\(CD = \frac{{\sqrt 5 }}{2}{\rm{\;cm}}\)
-
D.
\(CD = 2,5{\rm{\;cm}}\).
TH đồng dạng g-g: Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
Suy ra các cạnh tương ứng tỉ lệ.
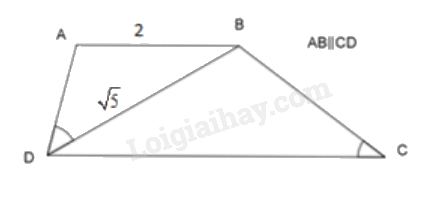
Vì \(AB\parallel CD\) nên: \(\widehat {ABD} = \widehat {BDC}\) (cặp góc so le trong)
Xét \(\Delta ADB\) và \(\Delta BCD\) ta có:
\(\begin{array}{l}\widehat {ABD} = \widehat {BDC}{\rm{(}}cmt{\rm{)}}\\\widehat {ADB} = \widehat {BCD}{\rm{\;(theo\;gt)}}\end{array}\)
Suy ra $\Delta ADB\backsim \Delta BCD\left( g-g \right)$
Do đó \(\frac{{AB}}{{BD}} = \frac{{DB}}{{CD}}\)
\(\begin{array}{l}\frac{2}{{\sqrt 5 }} = \frac{{\sqrt 5 }}{{CD}}\\CD = \frac{{\sqrt 5 \cdot \sqrt 5 }}{2} = \frac{5}{2} = 2,5{\rm{\;cm}}\end{array}\)
Đáp án D.
Đáp án : D
