Cho hình vuông ABCD. Gọi H, K lần lượt là trung điểm của AB, AD. Trên đường thẳng vuông góc với (ABCD) tại H, lấy điểm S. Chứng minh rằng:
a) \(AC \bot \left( {SHK} \right)\).
b) \(CK \bot \left( {SDH} \right)\).
+ Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) thì \(d \bot \left( P \right)\).
+ Nếu một đường thẳng vuông góc với một mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng đó.
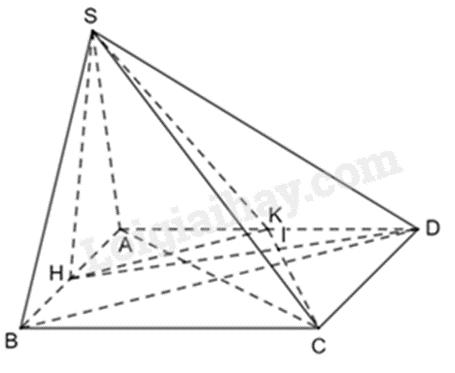
a) Vì H, K lần lượt là trung điểm của AB và AD nên HK là đường trung bình của tam giác ABD. Do đó, \(HK//BD\). Mà \(AC \bot BD\) (do ABCD là hình vuông) nên \(AC \bot HK\)
Vì \(AC \bot HK,SH \bot AC\left( {do\;AC \subset \left( {ABCD} \right)} \right) \Rightarrow AC \bot \left( {SHK} \right)\)
b) Gọi I là giao điểm của CK và DH.
Tam giác AHD và tam giác DKC có: \(AH = DK,\widehat {HAD} = \widehat {KDC},AD = DC\)
Do đó, \(\Delta AHD = \Delta DKC\left( {c.g.c} \right) \Rightarrow \widehat {HDA} = \widehat {KCD}\)
Ta có: \(\widehat {DKC} + \widehat {KCD} = {90^0} \Rightarrow \widehat {DKC} + \widehat {HDA} = {90^0}\)
Ta có: \(\widehat {DIK} = {180^0} - \left( {\widehat {DKC} + \widehat {HDA}} \right) = {90^0} \Rightarrow DH \bot CK\)
Mà \(SH \bot \left( {ABCD} \right),CK \subset \left( {ABCD} \right) \Rightarrow SH \bot CK\)
Ta có: \(DH \bot CK,SH \bot CK\), SH và DH nằm trong mặt phẳng (SHD) và cắt nhau tại H nên \(CK \bot \left( {SDH} \right)\).








Danh sách bình luận