Chọn khẳng định đúng.

Cho \(a > 0,m,n \in \mathbb{R}\). Khẳng định nào sau đây là đúng?

Chọn đáp án đúng.

Cho số dương a. Khi đó:

Chọn đáp án đúng:

Rút gọn biểu thức \(\frac{{{x^{\frac{4}{3}}}y + x{y^{\frac{4}{3}}}}}{{\sqrt[3]{x} + \sqrt[3]{y}}}\) (với \(x,y > 0\)) được kết quả là:

Giả sử cường độ ánh sáng I dưới mặt biển giảm dần theo độ sâu theo công thức \(I = {I_o}{a^d}\), trong đó \({I_o}\) là cường độ ánh sáng tại mặt nước biển, a là một hằng số dương, d là độ sâu tính từ mặt nước biển (tính bằng mét). Ở một vùng biển cường độ ánh sáng tại độ sâu 1m bằng 90% cường độ ánh sáng tại mặt nước biển. Giá trị của a là:

Chọn đáp án đúng.

Với \(a,b > 0\) thì:  

Chọn đáp án đúng.

Với \(0 < a \ne 1\) thì:

Trong Hóa học, độ pH của một dung dịch được tính theo công thức \(pH =  - \log \left[ {{H^ + }} \right]\), trong đó \(\left[ {{H^ + }} \right]\) là nồng độ ion hydrogen tính bằng mol/lít. Tính nồng độ pH của dung dịch có nồng độ ion hydrogen bằng 0,001 mol/lít.

Chọn đáp án đúng: (Các biểu thức trên đều có nghĩa)

Đồ thị hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) luôn:

Hàm số nào dưới đây là hàm số mũ cơ số 3?

Hàm số nào dưới đây không phải là hàm số lôgarit?  

Hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) liên tục trên:

Cho đồ thị các hàm số \(y = {a^x},y = {b^x},y = {\log _c}x\) như hình vẽ dưới

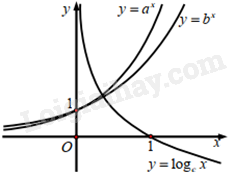
Khẳng định nào dưới đây là đúng?

Cho hàm số \(y = f\left( x \right) = {\log _{\sqrt 3 }}x\). Biết rằng: \(\mathop {\max }\limits_{x \in \left[ {3;9} \right]} y = M,\mathop {\min }\limits_{x \in \left[ {3;9} \right]} y = m\). Khi đó:

Bất phương trình \({a^x} > b\left( {0 < a \ne 1} \right)\) có tập nghiệm là \(\mathbb{R}\) khi:

Tập nghiệm của bất phương trình \({\left( {\sqrt 5 } \right)^x} > 5\) là:  

Phương trình \({\log _{\frac{1}{2}}}x =  - 2\) có nghiệm là:  

Nếu x và y thỏa mãn \({4^x} = 16\) và \({3^{x + y}} = 729\) thì y bằng: